1.DQN
DQN（Deep Q-Network）是一种将深度学习与强化学习中的Q-learning算法相结合的方法，用于解决高维状态空间下的决策问题。DQN能够在诸如Atari游戏等复杂任务中取得人类水平甚至超越人类的表现，成为深度强化学习发展中的一个重要里程碑。
DQN（Deep Q-Network）和Q-learning的核心思想都源于值迭代的强化学习方法，**目标都是学习一个最优的Q函数，用来指导智能体在给定状态下选择最优动作。**但它们在实现方式和适用场景上有显著区别。
- 传统Q-learning是一种表格型（tabular）方法，它**通过维护一个Q表来存储每个状态-动作对的估计值，并在与环境交互过程中不断更新这个表。**这种方法在状态和动作空间较小时有效，但当状态空间变得巨大（比如图像输入或连续状态）时，Q表会变得无法存储和更新，计算也变得不可行。
- DQN则是在Q-learning的基础上**引入了深度神经网络，用网络来近似Q函数，从而无需显式存储Q表。**这使得DQN能够处理高维甚至连续的状态空间，例如原始像素作为输入的Atari游戏。
DQN还引入了两项关键技术来稳定训练：一是经验回放（experience replay），即把过去的经验存入回放缓冲区并随机采样进行学习，减少数据间的相关性；二是目标网络（target network），即使用一个缓慢更新或定期同步的独立网络来计算Q目标值，避免训练过程中的剧烈波动。
- 经验回放：智能体在与环境交互过程中，将每一步的经验（通常包括当前状态、采取的动作、获得的奖励、下一个状态以及是否终止）存储在一个称为"回放缓冲区" （replay buffer）的记忆单元中。在训练神经网络时，并不是立即使用刚刚获得的经验进行学习，而是**从这个缓冲区中随机采样一批过去的经验（称为一个"经验回放批次"）来更新网络参数。**这种做法有几个关键好处，首先，它打破了数据之间的时序相关性。在强化学习中，连续的观察通常是高度相关的，如果直接按时间顺序训练，会导致神经网络训练不稳定；而随机采样使得训练数据更接近独立同分布（i.i.d.），符合大多数深度学习算法的假设。其次，经验回放提高了数据效率，因为同一条经验可以被多次使用，而不是用一次就丢弃。
- 目标网络：在标准的Q-learning或DQN中，神经网络需要根据当前估计的Q值来计算目标Q值（即"标签"），用于监督学习。然而，如果每次都用同一个网络既预测当前Q值又生成目标Q值，那么目标值会随着网络参数的快速更新而剧烈变动，导致训练过程不稳定甚至发散。 为了解决这个问题，DQN引入了目标网络：它是一个与主Q网络结构相同但参数更新更慢（或周期性更新）的独立网络，专门用来计算目标Q值。 具体来说，在计算目标值时，使用目标网络来评估下一状态的Q值，而**主网络则负责预测当前状态-动作对的Q值。**目标网络的参数通常每隔若干训练步才从主网络复制一次（硬更新），或者通过缓慢的指数移动平均方式更新（软更新，也叫Polyak平均）。
DQN的Q网络更新公式：
相应的，DQN 所最小化的均方 TD 误差目标函数为：
代码
这段代码实现了一个经验回放池(ReplayBuffer)类，主要用于深度强化学习中存储和回放经验数据。
- init：初始化一个固定容量的双端队列作为缓冲区
- add：将状态转换元组添加到缓冲区
- sample：随机采样一批数据用于训练
- size：返回当前缓冲区中的数据数量
python
class ReplayBuffer:
''' 经验回放池 '''
def __init__(self, capacity):
self.buffer = collections.deque(maxlen=capacity) # 队列,先进先出
def add(self, state, action, reward, next_state, done): # 将数据加入buffer
self.buffer.append((state, action, reward, next_state, done))
def sample(self, batch_size): # 从buffer中采样数据,数量为batch_size
transitions = random.sample(self.buffer, batch_size) # 随机采样batch条数据
state, action, reward, next_state, done = zip(*transitions)
return np.array(state), action, reward, np.array(next_state), done
def size(self): # 目前buffer中数据的数量
return len(self.buffer)这段代码实现了DQN算法。init初始化Q网络、目标网络、优化器及相关参数；take_action使用ε-贪婪策略选择动作；update从经验回放中采样数据，计算当前Q值与目标Q值，通过均方误差更新Q网络，并定期同步目标网络。
python
class Qnet(torch.nn.Module):
''' 只有一层隐藏层的Q网络 '''
def __init__(self, state_dim, hidden_dim, action_dim):
super(Qnet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
def forward(self, x):
x = F.relu(self.fc1(x)) # 隐藏层使用ReLU激活函数
return self.fc2(x)
class DQN:
''' DQN算法 '''
def __init__(self, state_dim, hidden_dim, action_dim, learning_rate, gamma, epsilon, target_update, device):
self.action_dim = action_dim
self.q_net = Qnet(state_dim, hidden_dim, self.action_dim).to(device) # Q网络
# 目标网络
self.target_q_net = Qnet(state_dim, hidden_dim, self.action_dim).to(device)
# 使用Adam优化器
self.optimizer = torch.optim.Adam(self.q_net.parameters(), lr=learning_rate)
self.gamma = gamma # 折扣因子
self.epsilon = epsilon # epsilon-贪婪策略
self.target_update = target_update # 目标网络更新频率
self.count = 0 # 计数器,记录更新次数
self.device = device
def take_action(self, state): # epsilon-贪婪策略采取动作
if np.random.random() < self.epsilon:
action = np.random.randint(self.action_dim)
else:
state = torch.tensor([state], dtype=torch.float).to(self.device)
action = self.q_net(state).argmax().item()
return action
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device) # 从经验回放缓冲区中提取一批经验数据（状态、动作、奖励、下一状态、完成标志）
actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device)
rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)
q_values = self.q_net(states).gather(1, actions) # Q值# 计算当前Q网络对这些状态-动作对的Q值估计
# 下个状态的最大Q值
max_next_q_values = self.target_q_net(next_states).max(1)[0].view(-1, 1) # 使用目标Q网络计算下一个状态的最大Q值
q_targets = rewards + self.gamma * max_next_q_values * (1 - dones) # TD误差目标 # 根据贝尔曼方程计算目标Q值
dqn_loss = torch.mean(F.mse_loss(q_values, q_targets)) # 均方误差损失函数
self.optimizer.zero_grad() # PyTorch中默认梯度会累积,这里需要显式将梯度置为0
dqn_loss.backward() # 反向传播更新参数
self.optimizer.step()
if self.count % self.target_update == 0: # 定期同步目标网络
self.target_q_net.load_state_dict(self.q_net.state_dict()) # 更新目标网络
self.count += 1训练主代码如下：
python
import random
import gym
import numpy as np
import collections
from tqdm import tqdm
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
import rl_utils
if __name__ == '__main__':
lr = 2e-3
num_episodes = 500
hidden_dim = 128
gamma = 0.98
epsilon = 0.01
target_update = 10
buffer_size = 10000
minimal_size = 500
batch_size = 64
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu") # 多卡cuda:0/1/2
env_name = 'CartPole-v0' # 环境名称
env = gym.make(env_name)
random.seed(0)
np.random.seed(0)
# env.seed(0)
torch.manual_seed(0)
replay_buffer = ReplayBuffer(buffer_size)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = DQN(state_dim, hidden_dim, action_dim, lr, gamma, epsilon, target_update, device)
return_list = []
for i in range(10):
with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
for i_episode in range(int(num_episodes / 10)):
episode_return = 0
# state = env.reset()
state = env.reset(seed=0)[0] if i == 0 and i_episode == 0 else env.reset()[0]
done = False
while not done:
action = agent.take_action(state)
# next_state, reward, done, _ = env.step(action)
next_state, reward, terminated, truncated, _ = env.step(action)
done = terminated or truncated
replay_buffer.add(state, action, reward, next_state, done)
state = next_state
episode_return += reward
# 当buffer数据的数量超过一定值后,才进行Q网络训练
if replay_buffer.size() > minimal_size:
b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)
transition_dict = {
'states': b_s,
'actions': b_a,
'next_states': b_ns,
'rewards': b_r,
'dones': b_d
}
agent.update(transition_dict)
return_list.append(episode_return)
if (i_episode + 1) % 10 == 0:
pbar.set_postfix({
'episode':
'%d' % (num_episodes / 10 * i + i_episode + 1),
'return':
'%.3f' % np.mean(return_list[-10:])
})
pbar.update(1)
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DQN on {}'.format(env_name))
plt.show()
mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DQN on {}'.format(env_name))
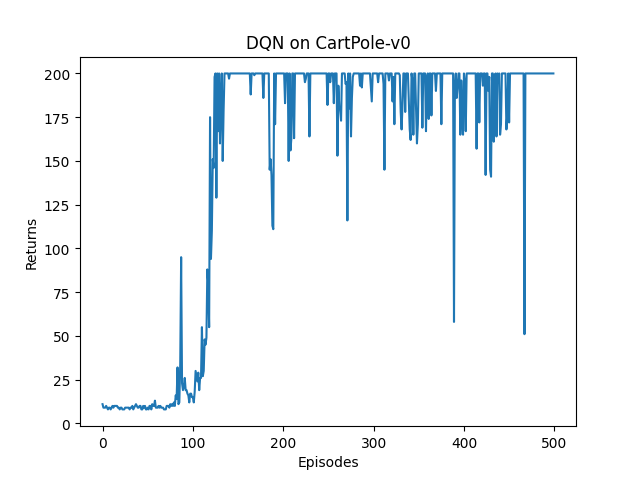
plt.show()DQN的奖励变化图如下：
DoubleDQN
Double DQN（Double Deep Q-Network）是在DQN基础上提出的一种改进方法，主要目的是解决DQN中存在的过估计（overestimation）问题。
在标准DQN中，计算目标Q值时，会选择下一状态中Q值最大的动作，并用这个最大Q值作为目标的一部分。 具体来说，目标值是： 。由于这个最大操作既用于选择动作又用于评估该动作的价值，容易导致对Q值的系统性高估，尤其在动作较多或噪声较大的情况下，这种过估计会累积，影响策略性能。
Double DQN通过将"动作选择"和"价值评估"这两个步骤解耦来缓解这个问题。它利用两个网络：主Q网络（用于选择动作）和目标网络（用于评估价值）。具体做法是：
- 用主Q网络（当前网络）在下一状态 s' 中选择使Q值最大的动作
；
- 然后用目标网络来评估这个动作的Q值，即目标值为：
这样，动作的选择和价值的评估分别由两个不同的网络完成，减少了因同一网络同时负责两者而导致的乐观偏差，从而显著降低过估计现象。
代码
python
class DQN:
''' DQN算法,包括Double DQN '''
def __init__(self, state_dim, hidden_dim, action_dim, learning_rate, gamma, epsilon, target_update, device, dqn_type='VanillaDQN'):
self.action_dim = action_dim
self.q_net = Qnet(state_dim, hidden_dim, self.action_dim).to(device)
self.target_q_net = Qnet(state_dim, hidden_dim, self.action_dim).to(device)
self.optimizer = torch.optim.Adam(self.q_net.parameters(), lr=learning_rate)
self.gamma = gamma
self.epsilon = epsilon
self.target_update = target_update
self.count = 0
self.dqn_type = dqn_type
self.device = device
def take_action(self, state):
if np.random.random() < self.epsilon:
action = np.random.randint(self.action_dim)
else:
state = torch.tensor([state], dtype=torch.float).to(self.device)
action = self.q_net(state).argmax().item()
return action
def max_q_value(self, state):
state = torch.tensor([state], dtype=torch.float).to(self.device)
return self.q_net(state).max().item()
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device)
rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)
q_values = self.q_net(states).gather(1, actions) # Q值
# 下个状态的最大Q值
if self.dqn_type == 'DoubleDQN': # DQN与Double DQN的区别
max_action = self.q_net(next_states).max(1)[1].view(-1, 1)
max_next_q_values = self.target_q_net(next_states).gather(1, max_action)
else: # DQN的情况
max_next_q_values = self.target_q_net(next_states).max(1)[0].view(-1, 1)
q_targets = rewards + self.gamma * max_next_q_values * (1 - dones) # TD误差目标
dqn_loss = torch.mean(F.mse_loss(q_values, q_targets)) # 均方误差损失函数
self.optimizer.zero_grad() # PyTorch中默认梯度会累积,这里需要显式将梯度置为0
dqn_loss.backward() # 反向传播更新参数
self.optimizer.step()
if self.count % self.target_update == 0:
self.target_q_net.load_state_dict(
self.q_net.state_dict()) # 更新目标网络
self.count += 1其中DoubleDQN和DQN算法中Q值的计算不同：
- DoubleDQN：先用主网络选择最优动作，再用目标网络评估该动作的Q值
- 普通DQN：直接用目标网络选择并评估最大Q值动作
python
q_values = self.q_net(states).gather(1, actions) # Q值
# 下个状态的最大Q值
if self.dqn_type == 'DoubleDQN': # DQN与Double DQN的区别
max_action = self.q_net(next_states).max(1)[1].view(-1, 1)
max_next_q_values = self.target_q_net(next_states).gather(1, max_action)
else: # DQN的情况
max_next_q_values = self.target_q_net(next_states).max(1)[0].view(-1, 1)Dueling Q
Dueling Q（通常称为 Dueling DQN 或 Dueling Network Architecture），其核心思想是将 Q 函数分解为两个部分：状态价值函数（Value function）和 优势函数（Advantage function），从而更高效、更准确地学习状态的价值和不同动作之间的相对优劣。
优势函数
优势函数（Advantage Function），通常记作 A(s, a)，是强化学习中用来衡量在某个状态 s 下，采取某个特定动作 a 相对于当前策略的平均表现好多少的一个量。
它的数学定义是：
其中：
- Q(s, a) 是动作价值函数，表示在状态 s 下执行动作 a 后，按照策略继续行动所能获得的期望累积回报；
- V(s) 是状态价值函数，表示在状态 s 下，按照当前策略行动所能获得的期望累积回报（即所有可能动作的加权平均）。
因此，优势函数 A(s, a) 表达的是：动作 a 比"平均水平"好（或差）多少。
- 如果 A(s, a) > 0，说明这个动作比在状态 s 下的平均动作更好；
- 如果 A(s, a) < 0，说明它比平均水平更差；
- 如果所有动作的优势都为 0，说明它们表现相当。
简而言之，优势函数帮助智能体区分"好动作"和"坏动作"，而不只是知道某个状态整体好不好，从而做出更精细的决策。
Dueling Ｑ
在标准 DQN 中，神经网络直接输出每个动作的 Q 值。而在 Dueling DQN 中，网络的最后几层被分为两个独立的流（streams）：
- 一个流估计状态价值函数 V(s)，它表示在状态 s 下未来累积回报的期望，不依赖于具体动作；
- 另一个流估计每个动作的优势函数 A(s, a)，它衡量在状态 s 下采取动作 a 相对于平均表现的好坏程度。
这两个流最终通过一个聚合层（通常使用 ）合并为最终的 Q 值，以保证 identifiability（可识别性），即 V 和 A 不能单独确定，但它们的组合 Q 是唯一确定的。
这种结构的优势在于：
- 在某些状态下，动作的选择对结果影响不大（比如游戏中的某些"等待"阶段），此时网络可以专注于学习准确的状态价值 V(s)，而无需对每个动作的细微差别过度建模；
- 在需要精细区分动作的状态下，优势流能更专注地学习动作间的相对优劣；
- 整体上提高了样本效率和策略的鲁棒性，尤其在动作不影响环境动态的场景中效果显著。
代码
python
class VAnet(torch.nn.Module):
''' 只有一层隐藏层的A网络和V网络 '''
def __init__(self, state_dim, hidden_dim, action_dim):
super(VAnet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim) # 共享网络部分
self.fc_A = torch.nn.Linear(hidden_dim, action_dim)
self.fc_V = torch.nn.Linear(hidden_dim, 1)
def forward(self, x):
A = self.fc_A(F.relu(self.fc1(x)))
V = self.fc_V(F.relu(self.fc1(x)))
Q = V + A - A.mean(1).view(-1, 1) # Q值由V值和A值计算得到
return Q主网络只需更换Qnet即可
python
class DuelingDQN:
''' DQN算法 '''
def __init__(self, state_dim, hidden_dim, action_dim, learning_rate, gamma, epsilon, target_update, device):
self.action_dim = action_dim
self.q_net = VAnet(state_dim, hidden_dim, self.action_dim).to(device) # Q网络
# 目标网络
self.target_q_net = VAnet(state_dim, hidden_dim, self.action_dim).to(device)
# 使用Adam优化器
self.optimizer = torch.optim.Adam(self.q_net.parameters(), lr=learning_rate)
self.gamma = gamma # 折扣因子
self.epsilon = epsilon # epsilon-贪婪策略
self.target_update = target_update # 目标网络更新频率
self.count = 0 # 计数器,记录更新次数
self.device = device
def take_action(self, state): # epsilon-贪婪策略采取动作
if np.random.random() < self.epsilon:
action = np.random.randint(self.action_dim)
else:
state = torch.tensor([state], dtype=torch.float).to(self.device)
action = self.q_net(state).argmax().item()
return action
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device) # 从经验回放缓冲区中提取一批经验数据（状态、动作、奖励、下一状态、完成标志）
actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device)
rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)
q_values = self.q_net(states).gather(1, actions) # Q值# 计算当前Q网络对这些状态-动作对的Q值估计
# 下个状态的最大Q值
max_next_q_values = self.target_q_net(next_states).max(1)[0].view(-1, 1) # 使用目标Q网络计算下一个状态的最大Q值
q_targets = rewards + self.gamma * max_next_q_values * (1 - dones) # 根据贝尔曼方程计算目标Q值 TD误差目标
dqn_loss = torch.mean(F.mse_loss(q_values, q_targets)) # 均方误差损失函数
self.optimizer.zero_grad() # PyTorch中默认梯度会累积,这里需要显式将梯度置为0
dqn_loss.backward() # 反向传播更新参数
self.optimizer.step()
if self.count % self.target_update == 0:
self.target_q_net.load_state_dict(self.q_net.state_dict()) # 更新目标网络
self.count += 1DDPG
DDPG（Deep Deterministic Policy Gradient，深度确定性策略梯度）是一种用于连续动作空间的深度强化学习算法 ，结合了策略梯度方法和Q学习思想，适用于高维状态和动作空间的控制任务（如机器人控制、自动驾驶等）。传统DQN只能处理离散动作，而许多现实问题（如控制机械臂的角度或速度）需要输出连续值的动作。DDPG正是为解决这一问题而设计的。
DDPG的核心思想是：
- 使用一个确定性策略
- 同时维护一个Critic网络 Q(s, a)，用来评估在状态 s 下执行动作 a 的长期回报（即Q值）；
- Actor通过Critic提供的梯度信息来更新策略，目标是最大化Q值；
- Critic则通过类似DQN的方式，用Bellman方程来更新Q函数。
DDPG有三个关键的技术：
-
DDPG采用了 Actor-Critic 框架 ，这种结构结合了策略梯度方法 和值函数方法 的优点，特别适合处理连续动作空间的强化学习问题。
- Actor 负责决策 ：它学习一个确定性策略
- Critic 负责评估：它学习一个动作价值函数 Q(s,a)，用于评估在状态 s 下执行动作 a 的长期回报好坏。
- 这种"一个做决策，一个打分"的机制，使得策略优化有了明确的反馈信号。
- Actor 负责决策 ：它学习一个确定性策略
-
DDPG在探索时通常通过对动作添加噪声 ：DDPG（Deep Deterministic Policy Gradient）采用的是确定性策略 ，也就是说，给定一个状态 s，策略网络
-
**软更新（Soft Update）：**在这些算法中，通常有两个网络： 主网络（如 Actor 或 Critic）：用于决策或评估，参数频繁更新； 目标网络：用于计算目标值（如 Bellman 目标），需要相对稳定以避免训练震荡。
不直接复制主网络的参数，而是缓慢地将目标网络向主网络"靠近" ，具体更新公式为：
其中：
这种方式使得目标网络的参数变化非常平缓，避免了因主网络剧烈更新而导致的目标值突变，从而显著提升训练的稳定性和收敛性。
代码
这段代码定义了一个策略网络类，用于强化学习中根据当前状态输出具体动作值。
- init：初始化网络结构，包含两个全连接层和动作边界值
- forward：前向传播过程，通过ReLU激活函数和tanh函数处理输入状态，最终输出限制在action_bound范围内的动作值
python
class PolicyNet(torch.nn.Module): # 策略网络Actor,输出给定状态下应该采取的具体动作值。
def __init__(self, state_dim, hidden_dim, action_dim, action_bound):
super(PolicyNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
self.action_bound = action_bound # action_bound是环境可以接受的动作最大值
def forward(self, x):
x = F.relu(self.fc1(x))
return torch.tanh(self.fc2(x)) * self.action_bound这段代码定义了一个Q值网络类，用于强化学习中的Critic网络：
- init方法初始化网络结构：输入层将状态和动作拼接后的向量映射到隐藏层，再通过两层全连接层最终输出一个标量Q值
- forward方法实现前向传播：首先将状态x和动作a在特征维度上拼接，然后依次通过两个ReLU激活的隐藏层，最后输出Q值估计
该网络用于评估特定状态下执行某个动作的价值。
python
class QValueNet(torch.nn.Module): # Q网络(Critic)的标准实现，用于评估给定状态-动作对的价值。
def __init__(self, state_dim, hidden_dim, action_dim):
super(QValueNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim + action_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, hidden_dim)
self.fc_out = torch.nn.Linear(hidden_dim, 1)
def forward(self, x, a):
cat = torch.cat([x, a], dim=1) # 拼接状态和动作
x = F.relu(self.fc1(cat))
x = F.relu(self.fc2(x))
return self.fc_out(x)
python
class DDPG:
''' DDPG算法 '''
def __init__(self, state_dim, hidden_dim, action_dim, action_bound, sigma, actor_lr, critic_lr, tau, gamma, device):
self.actor = PolicyNet(state_dim, hidden_dim, action_dim, action_bound).to(device)
self.critic = QValueNet(state_dim, hidden_dim, action_dim).to(device)
self.target_actor = PolicyNet(state_dim, hidden_dim, action_dim, action_bound).to(device)
self.target_critic = QValueNet(state_dim, hidden_dim, action_dim).to(device)
# 初始化目标价值网络并设置和价值网络相同的参数
self.target_critic.load_state_dict(self.critic.state_dict())
# 初始化目标策略网络并设置和策略相同的参数
self.target_actor.load_state_dict(self.actor.state_dict())
self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)
self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr)
self.gamma = gamma
self.sigma = sigma # 高斯噪声的标准差,均值直接设为0
self.tau = tau # 目标网络软更新参数
self.action_dim = action_dim
self.device = device
def take_action(self, state):
state = torch.tensor([state], dtype=torch.float).to(self.device)
action = self.actor(state).item()
# 给动作添加噪声，增加探索
action = action + self.sigma * np.random.randn(self.action_dim)
return action
def soft_update(self, net, target_net): # 软更新方式使目标网络缓慢跟踪主网络的变化，提高训练稳定性。
for param_target, param in zip(target_net.parameters(), net.parameters()):
param_target.data.copy_(param_target.data * (1.0 - self.tau) + param.data * self.tau)
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions'], dtype=torch.float).view(-1, 1).to(self.device)
rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)
next_q_values = self.target_critic(next_states, self.target_actor(next_states)) # 使用目标网络计算目标Q值
q_targets = rewards + self.gamma * next_q_values * (1 - dones)
critic_loss = torch.mean(F.mse_loss(self.critic(states, actions), q_targets)) # 更新Critic网络：最小化预测Q值与目标Q值的均方误差
self.critic_optimizer.zero_grad()
critic_loss.backward()
self.critic_optimizer.step()
actor_loss = -torch.mean(self.critic(states, self.actor(states))) # 更新Actor网络：最大化Q值（通过策略梯度）
self.actor_optimizer.zero_grad()
actor_loss.backward()
self.actor_optimizer.step()
self.soft_update(self.actor, self.target_actor) # 软更新策略网络
self.soft_update(self.critic, self.target_critic) # 软更新价值网络其中这段代码实现了DDPG算法中的动作选择功能为动作添加高斯噪声以增强探索能力
python
def take_action(self, state):
state = torch.tensor([state], dtype=torch.float).to(self.device)
action = self.actor(state).item()
# 给动作添加噪声，增加探索
action = action + self.sigma * np.random.randn(self.action_dim)
return action其中这段代码实现了DDPG算法中的软更新机制：。功能是让目标网络(target_net)缓慢跟踪主网络(net)的参数变化，通过tau参数控制更新幅度，从而提高训练稳定性。具体做法是将目标网络参数逐步向主网络参数靠近，而不是直接复制。
python
def soft_update(self, net, target_net): # 软更新方式使目标网络缓慢跟踪主网络的变化，提高训练稳定性。
for param_target, param in zip(target_net.parameters(), net.parameters()):
param_target.data.copy_(param_target.data * (1.0 - self.tau) + param.data * self.tau)Reinforce
REINFORCE 是一种经典的策略梯度（Policy Gradient）算法，属于蒙特卡洛（Monte Carlo）方法，其核心思想是：直接通过与环境交互获得的完整轨迹（episode），来估计策略的梯度，并以此更新策略参数，从而逐步提升期望回报。
基本目标：REINFORCE 试图直接优化策略 （由参数
参数化），以最大化期望累积回报：
，其中
是一个完整的轨迹（episode）。
策略梯度定理：根据策略梯度定理，目标函数 对参数
的梯度为：
这个公式说明：如果某个动作导致了高回报 ，就增加它被选择的概率；反之则降低。
REINFORCE 的更新步骤
- 执行策略：用当前策略
- 计算回报：从后往前计算每个时间步的
- 计算梯度估计：
- 更新策略参数**：
代码
这段代码实现了REINFORCE算法，用于策略梯度强化学习。主要功能包括：初始化策略网络和优化器、根据策略网络输出的动作概率分布采样执行动作、以及通过奖励回传更新策略网络参数。
python
class PolicyNet(torch.nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim):
super(PolicyNet, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
def forward(self, x):
x = F.relu(self.fc1(x))
return F.softmax(self.fc2(x), dim=1)
class REINFORCE:
def __init__(self, state_dim, hidden_dim, action_dim, learning_rate, gamma,
device):
self.policy_net = PolicyNet(state_dim, hidden_dim, action_dim).to(device)
self.optimizer = torch.optim.Adam(self.policy_net.parameters(), lr=learning_rate) # 使用Adam优化器
self.gamma = gamma # 折扣因子
self.device = device
def take_action(self, state): # 根据动作概率分布随机采样
state = torch.tensor([state], dtype=torch.float).to(self.device)
probs = self.policy_net(state)
action_dist = torch.distributions.Categorical(probs) # 创建分类分布对象，根据概率分布进行随机采样
action = action_dist.sample() # 返回采样的动作索引
return action.item()
def update(self, transition_dict):
reward_list = transition_dict['rewards']
state_list = transition_dict['states']
action_list = transition_dict['actions']
G = 0
self.optimizer.zero_grad()
for i in reversed(range(len(reward_list))): # 从最后一步算起
reward = reward_list[i]
state = torch.tensor([state_list[i]], dtype=torch.float).to(self.device)
action = torch.tensor([action_list[i]]).view(-1, 1).to(self.device)
log_prob = torch.log(self.policy_net(state).gather(1, action)) # 从概率分布中提取实际采取动作对应的概率值,计算该动作概率的对数
G = self.gamma * G + reward
loss = -log_prob * G # 每一步的损失函数
loss.backward() # 反向传播计算梯度
self.optimizer.step() # 梯度下降这段代码实现了强化学习的训练循环，通过与环境交互收集经验数据来训练强化学习智能体。
python
learning_rate = 1e-3
num_episodes = 1000
hidden_dim = 128
gamma = 0.98
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
env_name = "CartPole-v0"
env = gym.make(env_name)
# env.seed(0)
torch.manual_seed(0)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = REINFORCE(state_dim, hidden_dim, action_dim, learning_rate, gamma, device)
return_list = []
for i in range(10):
with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
for i_episode in range(int(num_episodes / 10)):
episode_return = 0
transition_dict = {
'states': [],
'actions': [],
'next_states': [],
'rewards': [],
'dones': []
}
# state = env.reset()
state = env.reset(seed=0)[0] if i == 0 and i_episode == 0 else env.reset()[0]
done = False
while not done: # 收集完整的数据（done=True才停止）
action = agent.take_action(state)
# next_state, reward, done, _ = env.step(action)
next_state, reward, terminated, truncated, _ = env.step(action)
done = terminated or truncated
transition_dict['states'].append(state)
transition_dict['actions'].append(action)
transition_dict['next_states'].append(next_state)
transition_dict['rewards'].append(reward)
transition_dict['dones'].append(done)
state = next_state
episode_return += reward
return_list.append(episode_return)
agent.update(transition_dict) # 智能体更新：使用收集的数据更新agent策略
if (i_episode + 1) % 10 == 0:
pbar.set_postfix({
'episode':
'%d' % (num_episodes / 10 * i + i_episode + 1),
'return':
'%.3f' % np.mean(return_list[-10:])
})
pbar.update(1)
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('REINFORCE on {}'.format(env_name))
plt.show()
mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('REINFORCE on {}'.format(env_name))
plt.show()SAC
SAC（Soft Actor-Critic，软演员-评论家）是一种基于最大熵强化学习框架的深度强化学习算法，专为连续动作空间设计，兼具高样本效率、稳定性和探索能力，在许多连续控制任务中表现优异，甚至成为当前主流的强化学习算法之一。
与传统强化学习只追求最大化累积回报不同，SAC 在优化目标中额外加入了一个熵项（entropy），目标函数变为：
其中：
最大化熵意味着鼓励策略保持随机性（即探索），避免过早收敛到次优解，同时提升鲁棒性和泛化能力。
SAC有两个关键的技术：
-
将最大熵原则 融入 Actor-Critic 框架：
-
重参数化（Reparameterization）：在很多模型中（比如 SAC），策略
重参数化技巧的核心思想：把随机性从网络参数中剥离出来，转移到一个独立的、固定的噪声变量上，使得采样过程变成一个确定性函数 + 外部噪声的形式，从而让梯度可以正常传播。
**双 Q 网络：**双 Q 网络（Twin Q Networks）是深度强化学习中一种用于减少 Q 值过估计（overestimation）并**提高训练稳定性**的技术。
背景：为什么需要双 Q 网络？
在 DQN、DDPG 等基于 Q 函数的算法中，目标值的计算依赖于对下一状态动作价值的最大化估计（如 或
）。但由于函数逼近误差、噪声或有限样本，Q 网络往往会系统性高估真实 Q 值。这种过估计会通过 Bellman 更新不断累积，导致策略学习偏离最优。
双 Q 网络引入两个结构相同但参数独立的 Q 网络 ： 和
。 在计算目标值或策略梯度时，取两个 Q 值中的较小者（或保守估计），以抑制过估计。
为什么取最小值能减少过估计？
单个 Q 网络倾向于高估；而两个独立训练的 Q 网络的高估方向通常是不相关的，取最小值会偏向更保守的估计，从而抵消部分正向偏差。
AC、DQN和REINFORCE有什么区别
DQN是对Q网络（Critic）进行更新，REINFORCE仅对策略网络（Actor），AC是对两个同时进行：
- DQN：DQN 没有显式的策略网络（Actor），它的策略是隐式的（比如 ε-greedy：选 Q 值最大的动作）。所有学习都集中在 Q 网络（即 Critic）上，通过最小化 TD 误差来更新：
- REINFORCE：只更新 Actor（策略网络），REINFORCE 没有 Critic，不估计价值函数。它直接用采样得到的**完整回报** G_t 作为信号，通过策略梯度更新策略网络：
- Actor-Critic (AC)：同时更新 Actor 和 Critic
- Actor（策略网络）：根据 Critic 提供的优势信号（如 TD 误差
- Critic（价值网络）：通过 TD 学习估计 V(s) 或 Q(s,a)，用 TD 误差更新：
- Actor（策略网络）：根据 Critic 提供的优势信号（如 TD 误差
代码
这段代码定义了一个连续动作策略网络PolicyNetContinuous（Actor网络），用于强化学习中根据状态输出动作及其对数概率。网络包含三个全连接层：第一个为共享隐藏层，后两个分别输出动作的均值和标准差。通过正态分布采样动作，并用tanh函数将动作压缩到指定范围，同时调整对数概率密度以匹配tanh变换后的分布。最终返回缩放后的动作及对应的对数概率。
python
class PolicyNetContinuous(torch.nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim, action_bound):
super(PolicyNetContinuous, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc_mu = torch.nn.Linear(hidden_dim, action_dim)
self.fc_std = torch.nn.Linear(hidden_dim, action_dim)
self.action_bound = action_bound
def forward(self, x):
x = F.relu(self.fc1(x))
mu = self.fc_mu(x)
std = F.softplus(self.fc_std(x))
dist = Normal(mu, std)
normal_sample = dist.rsample() # rsample()是重参数化采样
log_prob = dist.log_prob(normal_sample)
action = torch.tanh(normal_sample) # 用tanh函数将动作压缩到指定范围
# 计算tanh_normal分布的对数概率密度
log_prob = log_prob - torch.log(1 - torch.tanh(action).pow(2) + 1e-7) # 调整对数概率密度以匹配tanh变换后的分布。
action = action * self.action_bound
return action, log_prob # 最终返回缩放后的动作及对应的对数概率。这段代码定义了一个连续动作空间的Q值网络（Critic网络）：
- init方法：初始化网络结构，包含三个全连接层，输入维度为状态和动作的拼接维度
- forward方法：前向传播过程，将状态x和动作a拼接后依次通过两个隐藏层（ReLU激活），最后输出一个Q值
网络用于评估在给定状态下执行某个连续动作的优劣程度。
python
class QValueNetContinuous(torch.nn.Module):
def __init__(self, state_dim, hidden_dim, action_dim):
super(QValueNetContinuous, self).__init__()
self.fc1 = torch.nn.Linear(state_dim + action_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, hidden_dim)
self.fc_out = torch.nn.Linear(hidden_dim, 1)
def forward(self, x, a):
cat = torch.cat([x, a], dim=1)
x = F.relu(self.fc1(cat))
x = F.relu(self.fc2(x))
return self.fc_out(x)这段代码实现了Soft Actor-Critic (SAC)算法，用于处理连续动作空间的强化学习任务。它包含策略网络、两个Q网络及其目标网络，通过最小化均方误差更新Q网络，最大化期望回报与熵的权衡来更新策略网络，并使用软更新保持目标网络稳定。同时自动调节熵温度系数α以控制探索程度。
python
class SAC:
''' 处理连续动作的SAC算法 '''
def __init__(self, state_dim, hidden_dim, action_dim, action_bound, actor_lr, critic_lr, alpha_lr, target_entropy, tau, gamma, device):
# 策略网络
self.actor = PolicyNetContinuous(state_dim, hidden_dim, action_dim, action_bound).to(device)
# 第一个Q网络及其目标网络
self.critic_1 = QValueNetContinuous(state_dim, hidden_dim, action_dim).to(device)
self.target_critic_1 = QValueNetContinuous(state_dim, hidden_dim, action_dim).to(device)
# 第二个Q网络及其目标网络
self.critic_2 = QValueNetContinuous(state_dim, hidden_dim, action_dim).to(device)
self.target_critic_2 = QValueNetContinuous(state_dim, hidden_dim, action_dim).to(device)
# 初始化目标网络参数
self.target_critic_1.load_state_dict(self.critic_1.state_dict())
self.target_critic_2.load_state_dict(self.critic_2.state_dict())
# 网络优化器
self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)
self.critic_1_optimizer = torch.optim.Adam(self.critic_1.parameters(), lr=critic_lr)
self.critic_2_optimizer = torch.optim.Adam(self.critic_2.parameters(), lr=critic_lr)
# alpha参数相关（自动调节熵温度系数）
self.log_alpha = torch.tensor(np.log(0.01), dtype=torch.float, device=device)
self.log_alpha.requires_grad = True # 可以对alpha求梯度
self.log_alpha_optimizer = torch.optim.Adam([self.log_alpha], lr=alpha_lr)
self.target_entropy = target_entropy # 目标熵值
self.gamma = gamma
self.tau = tau
self.device = device
def calc_target(self, rewards, next_states, dones):
next_actions, next_log_probs = self.actor(next_states)
next_q1 = self.target_critic_1(next_states, next_actions) # 使用两个目标critic网络计算下一状态的Q值
next_q2 = self.target_critic_2(next_states, next_actions)
next_q = torch.min(next_q1, next_q2) # 使用两个目标critic网络计算下一状态的Q值
target_q = rewards + self.gamma * (next_q - self.log_alpha.exp() * next_log_probs) * (1 - dones) # 根据贝尔曼方程计算目标Q值，包含熵正则化项
return target_q
def soft_update(self, target_net, net):
for target_param, param in zip(target_net.parameters(), net.parameters()):
target_param.data.copy_(self.tau * param.data + (1 - self.tau) * target_param.data)
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions'], dtype=torch.float).view(-1, 1).to(self.device)
rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)
# 更新两个Q网络 计算目标Q值，并通过均方误差损失函数更新两个Q网络
target_q = self.calc_target(rewards, next_states, dones)
critic_1_q_values = self.critic_1(states, actions)
critic_1_loss = F.mse_loss(critic_1_q_values, target_q.detach())
critic_2_q_values = self.critic_2(states, actions)
critic_2_loss = F.mse_loss(critic_2_q_values, target_q.detach())
self.critic_1_optimizer.zero_grad()
critic_1_loss.backward()
self.critic_1_optimizer.step()
self.critic_2_optimizer.zero_grad()
critic_2_loss.backward()
self.critic_2_optimizer.step()
# 更新策略网络
new_actions, log_probs = self.actor(states)
q1_value = self.critic_1(states, new_actions)
q2_value = self.critic_2(states, new_actions)
actor_loss = torch.mean(self.log_alpha.exp() * log_probs - torch.min(q1_value, q2_value))
self.actor_optimizer.zero_grad()
actor_loss.backward()
self.actor_optimizer.step()
# 更新alpha参数（熵温度系数）
alpha_loss = torch.mean((log_probs + self.target_entropy).detach() * self.log_alpha.exp())
self.log_alpha_optimizer.zero_grad()
alpha_loss.backward()
self.log_alpha_optimizer.step()
# 软更新目标网络
self.soft_update(self.target_critic_1, self.critic_1)
self.soft_update(self.target_critic_2, self.critic_2)
def take_action(self, state):
state = torch.tensor([state], dtype=torch.float).to(self.device)
action, _ = self.actor(state)
return [action.item()] # 返回数组形式的动作值其中这段代码实现了SAC算法中目标Q值的计算：
- 通过actor网络获取下一状态的动作和对数概率
- 使用两个目标critic网络计算下一状态的Q值
- 取两个Q值的最小值以减少过估计
- 根据贝尔曼方程计算目标Q值，包含熵正则化项
- 考虑终止状态，返回最终目标Q值
self.log_alpha.exp() * next_log_probs 是熵正则化项。
- next_log_probs 是动作的对数概率(log probability)，next_log_probs 是 log π(a|s)
- self.log_alpha.exp() 是温度系数α的指数形式
- 两者的乘积 self.log_alpha.exp() * next_log_probs 是SAC算法中的熵正则化项。对应公式，熵正则化项是: α * H = -α * E[log π(a|s)]
python
def calc_target(self, rewards, next_states, dones):
next_actions, next_log_probs = self.actor(next_states)
next_q1 = self.target_critic_1(next_states, next_actions) # 使用两个目标critic网络计算下一状态的Q值
next_q2 = self.target_critic_2(next_states, next_actions)
next_q = torch.min(next_q1, next_q2) # 使用两个目标critic网络计算下一状态的Q值
target_q = rewards + self.gamma * (next_q - self.log_alpha.exp() * next_log_probs) * (1 - dones) # 根据贝尔曼方程计算目标Q值，包含熵正则化项
return target_q这段代码实现了SAC算法中策略网络的更新：
- new_actions, log_probs = self.actor(states) - 从策略网络采样新动作及对应的对数概率
- q1_value, q2_value - 分别计算两个Q网络对(状态,新动作)的价值估计
- actor_loss - 计算策略网络损失：最小化(α×log_prob - min(Q1,Q2))的期望值，其中α是温度参数
这是典型的最大熵强化学习策略更新方式。
python
# 更新策略网络
new_actions, log_probs = self.actor(states) # 从策略网络采样新动作及对应的对数概率
q1_value = self.critic_1(states, new_actions) # 分别计算两个Q网络对(状态,新动作)的价值估计
q2_value = self.critic_2(states, new_actions)
actor_loss = torch.mean(self.log_alpha.exp() * log_probs - torch.min(q1_value, q2_value)) # 计算策略网络损失这段代码计算SAC算法中温度参数α的损失函数。功能解释：
- log_probs：当前策略的动作对数概率
- self.target_entropy：目标熵值（通常为动作维度的负数）
- self.log_alpha.exp()：温度参数α的指数形式
- 损失函数通过梯度下降调整α值，使策略熵接近目标熵，实现自动温度调节
python
# 更新alpha参数（熵温度系数）
alpha_loss = torch.mean((log_probs + self.target_entropy).detach() * self.log_alpha.exp())
self.log_alpha_optimizer.zero_grad()
alpha_loss.backward()
self.log_alpha_optimizer.step()TRPO
TRPO（Trust Region Policy Optimization，信赖域策略优化）是一种稳定且高效的策略梯度算法。它的核心思想是：在更新策略时，限制新旧策略之间的变化幅度，确保策略更新"足够小"，从而保证性能单调提升、训练稳定。
为什么需要 TRPO？
标准策略梯度方法（如 REINFORCE、A2C）直接沿梯度方向更新策略参数：
但这种更新存在两个问题：
-
步长（学习率）难以选择：太大 → 策略崩溃；太小 → 收敛极慢；
-
策略更新后性能可能下降：因为策略梯度是局部线性近似，大步更新会偏离真实目标。
TRPO 的目标是：每次更新都保证新策略的期望回报不低于旧策略（即"单调改进"），同时尽可能高效地提升性能。
为此，TRPO提出了一个解决方法：信赖域约束（Trust Region）
TRPO 将策略优化转化为一个带约束的优化问题：
其中：
- 目标函数是重要性采样下的优势加权期望回报（即策略改进的近似）；
- 约束条件是：新旧策略在所有状态上的平均 KL 散度不超过阈值
这个约束确保新策略不会"偏离太远"，从而保持更新的可靠性。
关键技术：近似求解约束优化
直接求解上述问题很困难，TRPO 采用以下近似：
- 用一阶泰勒展开近似目标函数；
- 用二阶泰勒展开（Fisher 信息矩阵）近似 KL 散度约束；
- 将问题转化为自然梯度方向上的约束优化，最终解为：
其中：- g 是策略梯度（目标函数的一阶梯度）；
- F 是 Fisher 信息矩阵（KL 散度的 Hessian 近似）；
由于直接计算 开销大，TRPO 使用共轭梯度法（Conjugate Gradient）高效近似求解，并通过线搜索确保满足约束。
这里我们不给出TRPO的代码，建议读者直接研究PPO算法的代码
PPO
PPO（Proximal Policy Optimization，近端策略优化）是由 OpenAI 在 2017 年提出的一种高效、稳定且易于实现的策略梯度算法，现已成为深度强化学习中的主流方法之一。PPO是 TRPO 的简化与改进版，它在保持 TRPO（Trust Region Policy Optimization）核心思想------限制策略更新幅度以保证稳定------的同时，大幅简化了实现，避免了复杂的二阶优化计算。
核心目标 ：和所有策略梯度方法一样，PPO 的目标是最大化期望累积回报：。但关键在于：如何安全、高效地更新策略参数
，避免因更新步长过大导致性能崩溃。
基本思想 ：限制新旧策略的"距离"。如果新策略 和旧策略
差别太大，基于旧策略采集的数据就不再可靠，导致训练不稳定。 为此，PPO 引入了新旧策略的概率比（probability ratio）：
，这个比值衡量了新策略相对于旧策略对某个动作的偏好变化。
PPO 的两种主要形式
- Clipped Surrogate Objective（主流实现）：PPO 构造一个裁剪的目标函数，防止
其中：- clip 操作：当
- 取 min：确保更新总是保守的------只取"未裁剪"和"裁剪后"中更小的那个（对最大化问题而言是更"悲观"的估计）。
- 这种设计自动限制了策略更新的幅度：即使梯度很大，只要
- Adaptive KL Penalty（较少使用）：另一种形式是在目标函数中加入 KL 散度惩罚项：
优势函数
在 PPO（Proximal Policy Optimization）中，优势函数（Advantage Function）用于衡量"在某个状态下，采取某个动作比平均策略好多少"，是策略更新的关键信号。PPO 通常使用 GAE (Generalized Advantage Estimation，广义优势估计) 来计算优势函数，因为它能在偏差和方差之间取得良好平衡。
优势函数定义 为：
由于直接估计 较困难，PPO 采用 TD 误差的加权组合 来近似
，这就是 GAE。
GAE 的计算方式：GAE 通过结合多步 TD 误差（\\delta_t\^{(1)}, \\delta_t\^{(2)}, \\dots）来构造优势估计：
- 首先计算每一步的 TD 误差（1-step）：
- 然后递归计算 GAE 优势：
其中：
- 通常取
代码
这段代码实现了广义优势估计(GAE)算法。该算法用于强化学习中估计策略的优势函数。主要功能是：
- 将TD误差转换为numpy数组
- 从后往前计算优势函数值，使用公式：A_t = δ_t + γλA_{t+1}
- 将结果反转为正向顺序
- 返回PyTorch张量格式的优势函数值
python
def compute_advantage(gamma, lmbda, td_delta): # 广义优势估计(GAE)
td_delta = td_delta.detach().numpy()
advantage_list = []
advantage = 0.0
for delta in td_delta[::-1]: # 从后往前计算优势函数值
advantage = gamma * lmbda * advantage + delta # 使用公式：A_t = δ_t + γλA_{t+1}
advantage_list.append(advantage)
advantage_list.reverse()
return torch.tensor(advantage_list, dtype=torch.float)这段代码实现了PPO算法的初始化、动作选择和策略更新功能。其中compute_advantage用于计算广义优势估计(GAE)，update方法通过截断策略梯度更新Actor和Critic网络。
python
class PPO:
''' PPO算法,采用截断方式 '''
def __init__(self, state_dim, hidden_dim, action_dim, actor_lr, critic_lr, lmbda, epochs, eps, gamma, device):
self.actor = PolicyNet(state_dim, hidden_dim, action_dim).to(device)
self.critic = ValueNet(state_dim, hidden_dim).to(device)
self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)
self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr)
self.gamma = gamma
self.lmbda = lmbda
self.epochs = epochs # 一条序列的数据用来训练轮数
self.eps = eps # PPO中截断范围的参数
self.device = device
def take_action(self, state):
state = torch.tensor([state], dtype=torch.float).to(self.device)
probs = self.actor(state)
action_dist = torch.distributions.Categorical(probs)
action = action_dist.sample()
return action.item()
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(self.device)
rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1).to(self.device)
td_target = rewards + self.gamma * self.critic(next_states) * (1 - dones) # 计算TD目标值（即时奖励+折扣后的下一个状态价值）
td_delta = td_target - self.critic(states) # 计算TD误差（目标值与当前状态价值估计的差）
advantage = compute_advantage(self.gamma, self.lmbda, td_delta.cpu()).to(self.device) # 基于TD误差计算广义优势估计(GAE)
old_log_probs = torch.log(self.actor(states).gather(1, actions)).detach() # 计算并保存采取动作的旧策略对数概率
for _ in range(self.epochs):
log_probs = torch.log(self.actor(states).gather(1, actions)) # 计算当前策略下动作的对数概率
ratio = torch.exp(log_probs - old_log_probs) # 计算新旧策略概率比值
surr1 = ratio * advantage # 标准策略梯度项
surr2 = torch.clamp(ratio, 1 - self.eps, 1 + self.eps) * advantage # 截断后的策略梯度项（限制更新幅度）
actor_loss = torch.mean(-torch.min(surr1, surr2)) # PPO损失函数，取两项中的较小值
critic_loss = torch.mean(F.mse_loss(self.critic(states), td_target.detach())) # 价值网络的均方误差损失
self.actor_optimizer.zero_grad()
self.critic_optimizer.zero_grad()
actor_loss.backward()
critic_loss.backward()
self.actor_optimizer.step()
self.critic_optimizer.step()接下来进行训练
python
def moving_average(a, window_size):
cumulative_sum = np.cumsum(np.insert(a, 0, 0))
middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_size
r = np.arange(1, window_size-1, 2)
begin = np.cumsum(a[:window_size-1])[::2] / r
end = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1]
return np.concatenate((begin, middle, end))
def train_on_policy_agent(env, agent, num_episodes):
return_list = []
for i in range(10):
with tqdm(total=int(num_episodes/10), desc='Iteration %d' % i) as pbar:
for i_episode in range(int(num_episodes/10)):
episode_return = 0
transition_dict = {'states': [], 'actions': [], 'next_states': [], 'rewards': [], 'dones': []}
# state = env.reset()
state = env.reset()[0] if isinstance(env.reset(), tuple) else env.reset()
done = False
while not done:
action = agent.take_action(state)
# next_state, reward, done, _ = env.step(action)
next_state, reward, terminated, truncated, _ = env.step(action)
done = terminated or truncated
transition_dict['states'].append(state)
transition_dict['actions'].append(action)
transition_dict['next_states'].append(next_state)
transition_dict['rewards'].append(reward)
transition_dict['dones'].append(done)
state = next_state
episode_return += reward
return_list.append(episode_return)
agent.update(transition_dict)
if (i_episode+1) % 10 == 0:
pbar.set_postfix({'episode': '%d' % (num_episodes/10 * i + i_episode+1), 'return': '%.3f' % np.mean(return_list[-10:])})
pbar.update(1)
return return_list
actor_lr = 1e-3
critic_lr = 1e-2
num_episodes = 500
hidden_dim = 128
gamma = 0.98
lmbda = 0.95
epochs = 10
eps = 0.2
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
env_name = 'CartPole-v0'
env = gym.make(env_name)
# env.seed(0)
torch.manual_seed(0)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = PPO(state_dim, hidden_dim, action_dim, actor_lr, critic_lr, lmbda, epochs, eps, gamma, device)
return_list = train_on_policy_agent(env, agent, num_episodes)
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('PPO on {}'.format(env_name))
plt.show()
mv_return = moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('PPO on {}'.format(env_name))
plt.show()