【递归算法】二叉搜索树中第K小的元素

题目链接

文章摘要：

本文介绍了在二叉搜索树(BST)中查找第K小元素的两种解法。第一种解法利用BST中序遍历的有序性，通过全局变量count记录当前遍历次序，当count减至0时记录当前节点值。第二种解法在第一种基础上添加剪枝优化，当找到目标元素后直接终止后续遍历。两种方法都采用递归实现中序遍历，时间复杂度为O(n)，空间复杂度为O(h)(h为树高)。剪枝优化版本能提前终止遍历，效率更高。文章通过示例详细说明了算法流程，并提供了Java代码实现。

一、题目解析

题目要求找出一棵二叉搜索树（BST）的第K小的元素

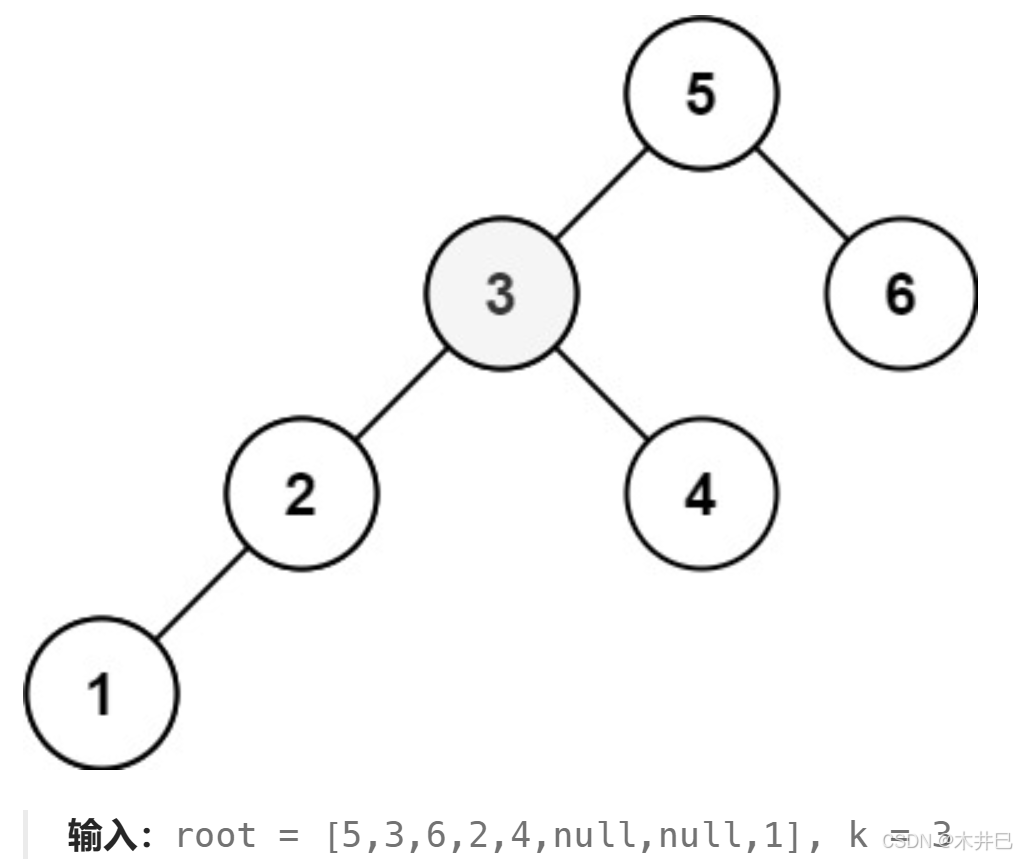
分析示例2：

要求BST的第3小的元素，我们对其进行中序遍历
中序遍历后得到的结果是：123456，其中的元素3就是我们要的目标

因此返回的结果就是：3

二、算法原理 + 代码实现

全局变量 + 中序遍历

从分析的示例我们初步得出的思路就是利用BST的性质（中序遍历的结果是一个由小到大的有序数字序列）对BST进行中序遍历。

但是，如何让计算机知道它正在遍历的节点是第几个节点呢？

我们可以使用一个全局变量来记录当前节点的序号，先让该全局变量等于K的值，然后在遍历的过程中先自减1 再对当前根节点（中序遍历：左 -> 当前根节点 -> 右）进行操作。

因为是递归，我们需要使用一个全局变量来记录结果。

因此我们的解题思路是：全局变量 + 中序遍历

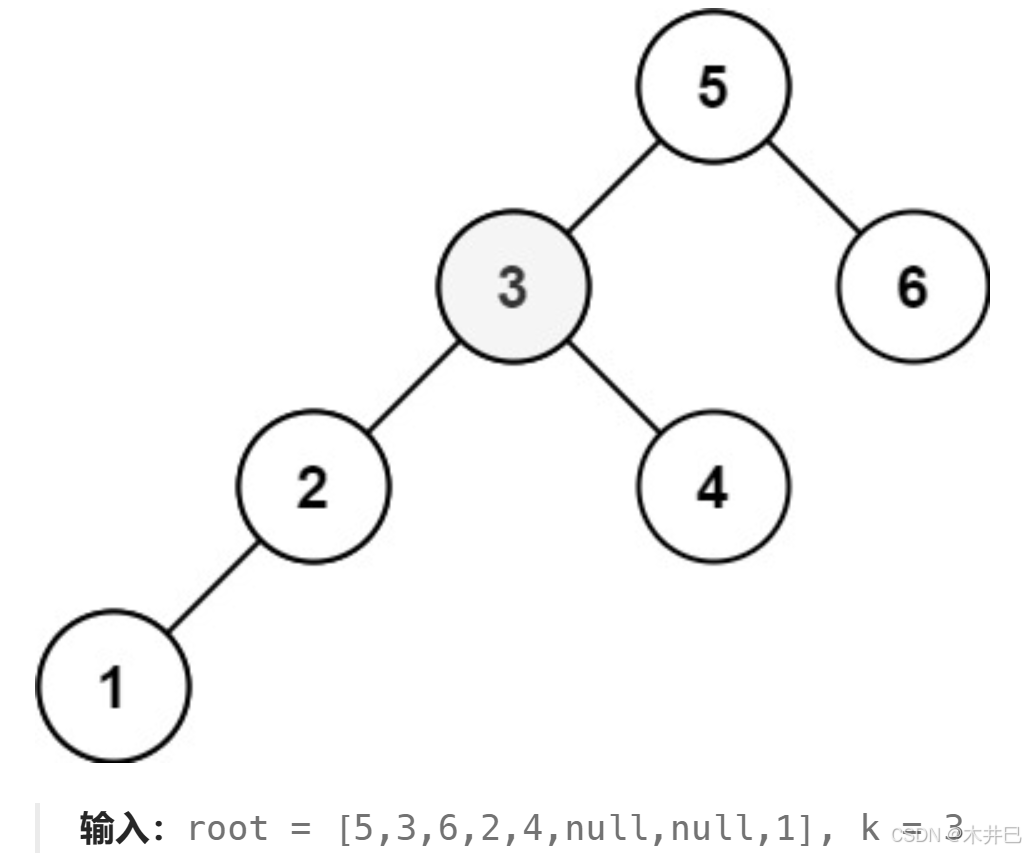
下面来模拟一遍示例2的过程：

从根节点5开始，先递归左子树3，到达左子树3后递归其左子树2，到达左子树2后递归其左子树1，到达左子树1后递归其左子树后，发现为空，返回到节点1处
将全局变量count赋值为K，则count = 3；全局变量ret赋值为0
现在处于节点1处，此时已经执行完节点1的左子树操作，需要执行根节点操作，在此之前先让count自减1，则count = 2。然后判断一下count是否为0，不为0则说明还未找到目标元素。继续递归节点1的右子树（也为空，返回到节点1之后再返回到节点2）
现在处于节点2处，此时已经执行完节点2的左子树操作，需要执行根节点操作，在此之前先让count自减1，则count = 1。然后判断一下count是否为0，不为0则说明还未找到目标元素。继续递归节点2的右子树（也为空，返回到节点2之后再返回到节点3）
现在处于节点3处，此时已经执行完节点3的左子树操作，需要执行根节点操作，在此之前先让count自减1，则count = 0。然后判断一下count是否为0，为0则说明当前节点的值就是目标元素。将当前节点的值赋值给ret。继续递归节点3的右子树...
后面的节点4、节点5和节点6也是如此操作，以此类推直至整棵二叉搜索树遍历完毕
遍历完成后，ret的值就是目标值，直接返回ret即可

总结该解法：

全局变量count	全局变量ret	中序遍历
用于判断当前遍历的节点是否为目标	记录目标元素	左：为了递归寻找目标节点；根：当遍历到目标节点时将当前节点的值赋值给ret，否则不进行操作；右：为了递归寻找目标节点

代码实现如下：

Java 复制代码

class Solution {
    int count = 0;
    int ret = 0;
    public int kthSmallest(TreeNode root, int k) {
        count = k;
        dfs(root);
        return ret;
    }

    private void dfs(TreeNode root) {
        // 递归出口
        if (root == null) return;

		// 左
        dfs(root.left);

        // 根
        count --;
        if (count == 0) ret = root.val;

        // 右
        dfs(root.right);
    }
}

全局变量 + 中序遍历 + 剪枝优化

剪枝优化主要是为了提高程序的效率，因为上面的解法在第6步的时候还需要再遍历节点4、节点5和节点6，但是目标元素已经找到了，也就是说后面的这三个节点已经没有遍历的必要了，所以我们可以直接将后面的操作省略，直接返回结果。

在左、根、右三个操作的前面分别增加一条if语句判断count，若count <= 0说明已经找到目标元素，此时就不需要继续递归了，直接返回。

全局变量count	全局变量ret	中序遍历	剪枝优化
用于判断当前遍历的节点是否为目标	记录目标元素	左：为了递归寻找目标节点；根：当遍历到目标节点时将当前节点的值赋值给ret，否则不进行操作；右：为了递归寻找目标节点	省去不必要的操作

剪枝优化版本的代码实现如下：

Java 复制代码

class Solution {
    int count = 0;
    int ret = 0;
    public int kthSmallest(TreeNode root, int k) {
        count = k;
        dfs(root);
        return ret;
    }

    private void dfs(TreeNode root) {
        // 递归出口
        if (root == null || count <= 0) return;

		// 左
        dfs(root.left);
	
		// 根
        if (count <= 0) return;
        count --;
        if (count == 0) ret = root.val;

		// 右
        if (count <= 0) return;
        dfs(root.right);
    }
}

若有错误请尽管指出~ 😊🌹

完