Leetcode 120 求根节点到叶节点数字之和 | 完全二叉树的节点个数

im_AMBER2026-02-14 10:48

1 题目

129. 求根节点到叶节点数字之和

给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。

每条从根节点到叶节点的路径都代表一个数字：

  • 例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。

计算从根节点到叶节点生成的 所有数字之和 。

叶节点 是指没有子节点的节点。

示例 1：

复制代码 
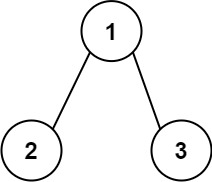
输入：root = [1,2,3]
输出：25
解释：
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此，数字总和 = 12 + 13 = 25

示例 2：

复制代码 
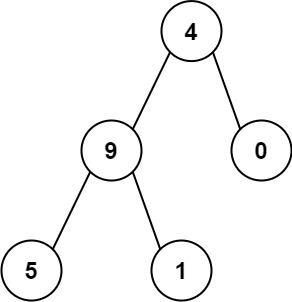
输入：root = [4,9,0,5,1]
输出：1026
解释：
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此，数字总和 = 495 + 491 + 40 = 1026

提示：

  • 树中节点的数目在范围 [1, 1000] 内
  • 0 <= Node.val <= 9
  • 树的深度不超过 10

2 代码实现

c++

cpp 复制代码 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private: 
    int dfs (TreeNode* node ,int curSum){
        if (node == nullptr){
            return 0 ;
        }

        curSum = curSum * 10 + node -> val;

        if (node -> left == nullptr && node -> right == nullptr){
            return curSum ;
        }

        return dfs(node -> left ,curSum) + dfs(node -> right , curSum);
    }
public:
    int sumNumbers(TreeNode* root) {
        return dfs (root, 0);
    }
};

js

javascript 复制代码 
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var sumNumbers = function(root) {
    const dfs = function (node, curSum){
        if (node == null){
            return 0 ;
        }
        curSum = curSum * 10 + node.val ;
        if (node.left == null && node.right == null){
            return curSum ;
        }
        return dfs(node.left , curSum) + dfs(node.right , curSum);
    }
    return dfs(root , 0 );
};

思考

怎么将根节点到叶子节点的遍历数字记录下来，如何记录树的深度。可以先存成字符串在转换吗？还是要怎么做，不知道怎么实现？

题解

解题思路

解决这个问题的核心是深度优先搜索（DFS）：

  1. 从根节点开始，递归遍历每个节点；
  2. 每访问一个节点，就将当前累积的数字 *10 + 当前节点值（比如路径 1->2，就是 1*10+2=12）；
  3. 当遍历到叶节点（左右子节点都为空）时，将当前累积的数字加入总和；
  4. 递归遍历左子树和右子树，最终得到所有路径的数字之和。

这种方式不需要额外记录树的深度，也不需要字符串转换，直接通过数值运算完成，效率更高。

C++ 完整代码实现

cpp 复制代码 
#include <iostream>
using namespace std;

// 定义二叉树节点结构
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    int sumNumbers(TreeNode* root) {
        // 调用递归函数，初始累积值为0
        return dfs(root, 0);
    }

private:
    // 深度优先搜索递归函数：node为当前节点，currentSum为到当前节点的累积数字
    int dfs(TreeNode* node, int currentSum) {
        // 边界条件：节点为空，返回0（无贡献）
        if (node == nullptr) {
            return 0;
        }

        // 计算到当前节点的累积数字：前序值*10 + 当前节点值
        currentSum = currentSum * 10 + node->val;

        // 叶节点：左右子节点都为空，返回当前累积的数字（这条路径的最终值）
        if (node->left == nullptr && node->right == nullptr) {
            return currentSum;
        }

        // 非叶节点：递归遍历左子树和右子树，求和
        return dfs(node->left, currentSum) + dfs(node->right, currentSum);
    }
};

// 测试用例
int main() {
    // 示例1：root = [1,2,3]
    TreeNode* root1 = new TreeNode(1);
    root1->left = new TreeNode(2);
    root1->right = new TreeNode(3);
    Solution s;
    cout << "示例1输出：" << s.sumNumbers(root1) << endl; // 预期输出25

    // 示例2：root = [4,9,0,5,1]
    TreeNode* root2 = new TreeNode(4);
    root2->left = new TreeNode(9);
    root2->right = new TreeNode(0);
    root2->left->left = new TreeNode(5);
    root2->left->right = new TreeNode(1);
    cout << "示例2输出：" << s.sumNumbers(root2) << endl; // 预期输出1026

    // 释放内存（避免内存泄漏）
    delete root1->left;
    delete root1->right;
    delete root1;
    delete root2->left->left;
    delete root2->left->right;
    delete root2->left;
    delete root2->right;
    delete root2;

    return 0;
}

代码关键部分解释

  1. 二叉树节点定义：符合题目中树的结构，包含值、左子节点、右子节点；
  2. sumNumbers 函数 ：对外接口，调用递归函数dfs，初始累积值为 0；
  3. dfs 递归函数 ：
    • 边界处理：节点为空时返回 0，避免空指针访问；
    • 累积计算：currentSum * 10 + node->val 是核心，比如路径 1->2，先算 010+1=1，再算 110+2=12；
    • 叶节点判断：左右子节点都为空时，当前累积值就是这条路径的数字，直接返回；
    • 递归遍历：非叶节点时，递归处理左右子树，将结果相加（所有路径的和）；
  4. 测试用例：还原题目中的两个示例，验证代码正确性。

补充：你提到的 "字符串存储" 方案（备选）

如果想先用字符串存储路径再转换，也可以实现（效率稍低，但逻辑更直观），核心代码如下：

cpp 复制代码 
class Solution {
public:
    int sum = 0; // 存储总和
    int sumNumbers(TreeNode* root) {
        string path = "";
        dfs_str(root, path);
        return sum;
    }

    void dfs_str(TreeNode* node, string path) {
        if (node == nullptr) return;
        path += to_string(node->val); // 拼接当前节点值到路径字符串
        // 叶节点：转换字符串为数字，加入总和
        if (node->left == nullptr && node->right == nullptr) {
            sum += stoi(path);
            return;
        }
        // 递归遍历左右子树
        dfs_str(node->left, path);
        dfs_str(node->right, path);
    }
};

总结

  1. 核心解法是深度优先搜索（DFS），遍历所有根到叶的路径；
  2. 推荐用数值累加 （currentSum * 10 + node->val）的方式，无需字符串转换，效率更高；
  3. 递归终止条件：节点为空返回 0，叶节点返回当前累积值，非叶节点返回左右子树结果之和。

这个实现满足题目所有约束（节点数≤1000、深度≤10），时间复杂度 O (n)（每个节点遍历一次），空间复杂度 O (h)（h 为树的深度，递归栈空间）。

3 题目

222. 完全二叉树的节点个数

给你一棵完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层（从第 0 层开始），则该层包含 1~ 2h 个节点。

示例 1：

复制代码 
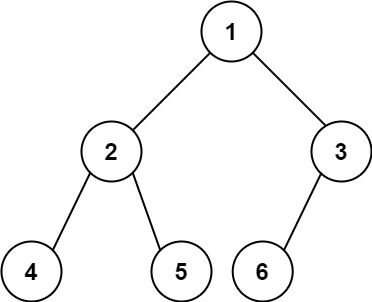
输入：root = [1,2,3,4,5,6]
输出：6

示例 2：

复制代码 
输入：root = []
输出：0

示例 3：

复制代码 
输入：root = [1]
输出：1

提示：

  • 树中节点的数目范围是[0, 5 * 104]
  • 0 <= Node.val <= 5 * 104
  • 题目数据保证输入的树是 完全二叉树

进阶： 遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗？

4 代码实现

c++

cpp 复制代码 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        if (root == nullptr){
            return 0 ;
        }
        int left = countNodes(root -> left );
        int right = countNodes(root -> right );
        return left + right + 1 ;
    }
};
cpp 复制代码 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        if (root == nullptr){
            return 0 ;
        }
        int leftHeight = 0 ; 
        TreeNode* leftNode = root -> left ;
        while (leftNode != nullptr){
            leftHeight ++ ;
            leftNode = leftNode -> left ;
        }

        int rightHeight = 0 ;
        TreeNode* rightNode = root -> right ;
        while(rightNode != nullptr){
            rightHeight ++ ;
            rightNode = rightNode ->right ;
        }

        if (leftHeight == rightHeight ){
            return (1 << (leftHeight + 1) ) - 1  ;
        }
        return 1 + countNodes(root -> left ) + countNodes(root -> right);
    }
};

js

javascript 复制代码 
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var countNodes = function(root) {
    if (root == null){
        return 0 ;
    }
    let left = countNodes(root.left);
    let right = countNodes(root.right);
    return 1 + left + right ;
};
javascript 复制代码 
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var countNodes = function(root) {
    if (root == null){
        return 0 ;
    }
    let leftNode = root.left;
    let leftHeight = 0 ;
    while (leftNode != null){
        leftHeight++;
        leftNode = leftNode.left ;
    }
    let rightNode = root.right ;
    let rightHeight = 0 ;
    while (rightNode != null){
        rightHeight ++ ;
        rightNode = rightNode.right ;
    }
    if (leftHeight == rightHeight ){
        return ( 1 << (leftHeight + 1)) - 1;
    }
    return 1 + countNodes(root.left) + countNodes(root.right);
};

思考

这个问题同样也是深度优先搜索，不知道怎么递归，完全二叉树只有最底下一层不是满的。终止条件是，如果一个节点的左右孩子节点不是全满，那么说明已经找到了有缺失的叶子节点的最后一层。

也还是不知道怎么写。

题解

看了思路但还是写不出代码，核心问题是对递归的 "终止条件""递归逻辑" 和 "完全二叉树特性的落地" 没有拆解得足够细。

从最基础的暴力 DFS 开始，再到进阶优化版，每个代码行都解释清楚，确保你能跟着写出来。

先明确核心问题：你写不出来的根源

  1. 不知道递归该 "返回什么"（终止条件模糊）；
  2. 不知道递归该 "算什么"（核心逻辑没落地）；
  3. 完全二叉树的特性不知道怎么转化为代码（比如 "怎么判断满二叉树""怎么算高度"）。

第一步：先搞定「暴力 DFS 版」（O (n)）------ 先保证能写出来

这个版本不利用完全二叉树特性，就是通用的 "统计二叉树节点数" 方法，逻辑最简单，是所有递归的基础，先把这个写会。

核心思路（暴力版）

递归的本质是 "分解问题"：

  • 一个树的节点数 = 1（当前节点） + 左子树的节点数 + 右子树的节点数；
  • 终止条件：如果节点是空的（nullptr），说明没有节点，返回 0。

C++ 完整代码（暴力版）

cpp 复制代码 
#include <iostream>
using namespace std;

// 二叉树节点定义（题目给定，不用改）
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    int countNodes(TreeNode* root) {
        // 步骤1：递归终止条件 ------ 空节点，节点数为0
        if (root == nullptr) {
            return 0;
        }
        // 步骤2：核心逻辑 ------ 当前节点(1) + 左子树节点数 + 右子树节点数
        int leftCount = countNodes(root->left);  // 递归算左子树
        int rightCount = countNodes(root->right); // 递归算右子树
        return 1 + leftCount + rightCount;       // 汇总
    }
};

// 测试代码（直接复制就能运行）
int main() {
    // 示例1：root = [1,2,3,4,5,6]
    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->left->left = new TreeNode(4);
    root->left->right = new TreeNode(5);
    root->right->left = new TreeNode(6);

    Solution s;
    cout << "节点总数：" << s.countNodes(root) << endl; // 输出6

    // 释放内存（可选，避免内存泄漏）
    delete root->left->left;
    delete root->left->right;
    delete root->left;
    delete root->right->left;
    delete root->right;
    delete root;

    return 0;
}

逐行解释（暴力版）------ 确保你能看懂每一步

  1. 节点定义 ：TreeNode 是题目给定的结构，记住就行，不用自己想；
  2. 终止条件 if (root == nullptr) ：
    • 比如递归到叶子节点的左孩子（空），这时候返回 0，说明这个位置没有节点；
    • 这是递归的 "出口"，没有这个会无限递归，必须写；
  3. leftCount = countNodes(root->left) ：
    • 把 "统计左子树节点数" 的问题，交给递归函数自己解决；
    • 你不用管递归到底怎么算的，只需要知道：调用这个函数，就能得到左子树的节点数；
  4. return 1 + leftCount + rightCount ：
    • 1 是当前节点自己；
    • leftCount 是左子树所有节点；
    • rightCount 是右子树所有节点；
    • 三者相加就是当前树的总节点数。

暴力版怎么练？------ 手把手教你写

  1. 先写函数头：int countNodes(TreeNode* root)；
  2. 先写终止条件：if (root == nullptr) return 0;；
  3. 再写递归计算左右子树：int left = countNodes(root->left); int right = countNodes(root->right);；
  4. 最后返回总和：return 1 + left + right;。

这个版本你一定要先写出来，哪怕抄一遍，也能建立 "递归能写出来" 的信心。

第二步：进阶版（利用完全二叉树特性，O (log²n)）------ 理解 "为什么快"

题目要求 "更快的算法"，核心是利用完全二叉树的特性：

完全二叉树 = 除了最后一层，其他层都是满的；最后一层的节点都靠左。

先记住 2 个关键公式 / 结论

  1. 满二叉树节点数公式 ：如果一棵满二叉树的高度是 h（高度定义：从根到叶子的层数，根是第 1 层），节点数 = 2^h - 1；
    • 比如高度为 3 的满二叉树：2^3 -1 = 7 个节点；
    • 高度为 2 的满二叉树：2^2 -1 = 3 个节点；
  2. 完全二叉树的高度计算 ：
    • 左高度：从当前节点一直往左走，能走几步，就是左高度（因为完全二叉树靠左）；
    • 右高度：从当前节点一直往右走，能走几步，就是右高度；
  3. 判断满二叉树 ：如果一个节点的左高度 == 右高度 → 这个树是满二叉树，直接用公式算节点数；
    • 如果左高度 > 右高度 → 右子树是满二叉树，左子树需要递归算。

C++ 完整代码（进阶版）

cpp 复制代码 
#include <iostream>
using namespace std;

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    int countNodes(TreeNode* root) {
        // 步骤1：终止条件 ------ 空节点返回0（和暴力版一样）
        if (root == nullptr) {
            return 0;
        }

        // 步骤2：计算左高度（一直往左走）
        int leftHeight = 0;
        TreeNode* leftNode = root->left;
        while (leftNode != nullptr) {
            leftHeight++;
            leftNode = leftNode->left; // 完全二叉树，往左走到底就是高度
        }

        // 步骤3：计算右高度（一直往右走）
        int rightHeight = 0;
        TreeNode* rightNode = root->right;
        while (rightNode != nullptr) {
            rightHeight++;
            rightNode = rightNode->right; // 往右走到底
        }

        // 步骤4：判断是否是满二叉树
        if (leftHeight == rightHeight) {
            // 满二叉树节点数公式：2^(leftHeight+1) - 1（因为leftHeight是从0开始算的）
            // 用位运算：1 << (leftHeight+1) 等价于 2^(leftHeight+1)，更快
            return (1 << (leftHeight + 1)) - 1;
        }

        // 步骤5：不是满二叉树，递归算左右子树（和暴力版一样，但次数少很多）
        return 1 + countNodes(root->left) + countNodes(root->right);
    }
};

// 测试代码（和暴力版一样）
int main() {
    TreeNode* root = new TreeNode(1);
    root->left = new TreeNode(2);
    root->right = new TreeNode(3);
    root->left->left = new TreeNode(4);
    root->left->right = new TreeNode(5);
    root->right->left = new TreeNode(6);

    Solution s;
    cout << "节点总数：" << s.countNodes(root) << endl; // 输出6

    // 释放内存
    delete root->left->left;
    delete root->left->right;
    delete root->left;
    delete root->right->left;
    delete root->right;
    delete root;

    return 0;
}

进阶版逐行解释（重点拆 "特性怎么落地"）

  1. 计算左 / 右高度 ：
    • 比如示例 1 的根节点：
      • 左高度：root->left（2）→ root->left->left（4）→ 再往左是 null，所以 leftHeight=2；
      • 右高度：root->right（3）→ 再往右是 null，所以 rightHeight=1；
    • 因为 leftHeight != rightHeight，所以不是满二叉树，需要递归；
    • 如果是满二叉树（比如 root=[1,2,3]），leftHeight=1，rightHeight=1，直接返回(1<<2)-1=3；
  2. 位运算 1 << (leftHeight+1) ：
    • 1 << n 表示把 1 左移 n 位，等价于 2^n，比如1<<3=8（2^3）；
    • 为什么是leftHeight+1？因为 leftHeight 是从 0 开始算的（比如走了 2 步，高度是 3 层）；
  3. 为什么更快 ：
    • 暴力版要遍历所有 n 个节点；
    • 进阶版每次递归都能排除一半的节点（因为有一侧是满二叉树，直接公式算），时间复杂度从 O (n) 降到 O (log²n)。

进阶版怎么写？------ 按步骤来

  1. 先写终止条件：if (root == nullptr) return 0;；

  2. 写循环算左高度：

    cpp 复制代码 
    int leftH = 0;
TreeNode* l = root->left;
while (l) { leftH++; l = l->left; }

  3. 写循环算右高度：

    cpp 复制代码 
    int rightH = 0;
TreeNode* r = root->right;
while (r) { rightH++; r = r->right; }

  4. 写满二叉树判断：if (leftH == rightH) return (1 << (leftH+1)) -1;；

  5. 最后递归：return 1 + countNodes(root->left) + countNodes(root->right);。

为什么你之前写不出来？------ 针对性解决

  1. 递归终止条件没先写 ：
    • 写递归的第一步，先想 "什么时候停"，而不是先想 "怎么算"；
    • 比如这道题，先写if (root == nullptr) return 0;，这是所有递归的基础；
  2. 把问题拆太小 ：
    • 不要一上来就想 "整个树怎么算"，而是想 "当前节点该算什么"；
    • 当前节点只需要做 3 件事：① 判断是不是空；② 算左右子树；③ 加自己；
  3. 完全二叉树特性没转化为代码 ：
    • 不要只记 "最后一层不满"，而是记 "怎么判断满二叉树"（左右高度相等）、"怎么算高度"（一直往左 / 右走）；
    • 先写暴力版，再在暴力版基础上加 "高度计算 + 满二叉树判断"，一步步改，不是一步到位。

总结（核心要点，记下来）

  1. 暴力版（必掌握） ：
    • 终止条件：空节点返回 0；
    • 递归逻辑：1 + 左子树节点数 + 右子树节点数；
  2. 进阶版（优化） ：
    • 左高度 = 一直往左走的步数，右高度 = 一直往右走的步数；
    • 左高度 == 右高度 → 满二叉树，用公式(1 << (h+1)) -1；
    • 否则递归算左右子树；
  3. 写代码的顺序：先写终止条件 → 再写核心逻辑（暴力版） → 再加优化（进阶版）。

你现在先把暴力版代码抄一遍，运行成功，再试着自己写一遍；然后在暴力版基础上，加高度计算的代码，改成进阶版。每一步都确保能运行，不要跳步，这样就能慢慢找到感觉了。如果哪一步写不出来，比如 "循环算高度"，随时问，我再拆细。

基础版

cpp 复制代码 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        if (root == nullptr){
            return 0 ;
        }
        int left = countNodes(root -> left );
        int right = countNodes(root -> right );
        return left + right + 1 ;
    }
};

进阶版

自己乱写又是错的

cpp 复制代码 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        if (root == nullptr){
            return 0 ;
        }
        int leftHeight = 0 ; 
        while (root -> left != nullptr){
            leftHeight ++ ;
            root = root -> left ;
        }

        int rightHeight = 0 ;
        while (root -> right != nullptr){
            rightHeight ++ ;
            root = root ->right ;
        }

        if (leftHeight == rightHeight ){
            return (1 << (leftHeight + 1) - 1 ) ;
        }
        return 1 + countNodes(root -> left ) + countNodes(root -> right);
    }
};

你写的代码思路方向是对的，但有两个致命错误导致逻辑完全走偏，我先指出问题，再给你修正后的完整代码，最后逐行解释错误原因，确保你能彻底理解。

核心错误分析

错误 1：修改了原始的 root 指针（最关键）

你在计算 leftHeight 时，直接把 root = root->left，这会让 root 指针指向左子树的最深处（比如示例 1 的根节点最后会指向 4），后续计算 rightHeight 和递归时，用的已经不是原来的根节点了，而是被修改后的节点，逻辑直接错乱。

错误 2：位运算优先级错误

(1 << (leftHeight + 1) - 1 ) 中，减法 -1 的优先级高于位运算 <<，导致实际计算的是 1 << (leftHeight + 1 - 1) = 1 << leftHeight，而不是正确的 (1 << (leftHeight + 1)) - 1，公式完全错了。

修正后的完整代码

cpp 复制代码 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        // 终止条件：空节点返回0
        if (root == nullptr) {
            return 0;
        }

        // 错误1修复：用临时变量计算高度，不修改原始root
        int leftHeight = 0;
        TreeNode* leftNode = root->left; // 临时变量，遍历左子树
        while (leftNode != nullptr) {
            leftHeight++;
            leftNode = leftNode->left; // 移动临时变量，不影响root
        }

        int rightHeight = 0;
        TreeNode* rightNode = root->right; // 临时变量，遍历右子树
        while (rightNode != nullptr) {
            rightHeight++;
            rightNode = rightNode->right; // 移动临时变量，不影响root
        }

        // 错误2修复：给位运算加括号，保证优先级
        if (leftHeight == rightHeight) {
            return (1 << (leftHeight + 1)) - 1; 
        }

        // 递归计算左右子树，此时root还是原始根节点，正确
        return 1 + countNodes(root->left) + countNodes(root->right);
    }
};

逐行解释错误修复细节

错误 1 修复：临时变量代替原始 root
cpp 复制代码 
// 你的错误写法（修改了root）
while (root -> left != nullptr){
    leftHeight ++ ;
    root = root -> left ; // root被改成左子节点，后续全错
}

// 正确写法（用临时变量）
TreeNode* leftNode = root->left; // 临时变量指向root的左子树
while (leftNode != nullptr) {
    leftHeight++;
    leftNode = leftNode->left; // 只移动临时变量，root不变
}
  • 比如示例 1 的根节点是 1，计算左高度时：
    • 你的写法：root 最终会变成 4（左子树最深处），后续计算右高度时，是用 4 的右节点（null），rightHeight=0，然后递归时 root->left 是 null，结果完全错；
    • 正确写法：root 始终是 1，leftNode 遍历完左子树后销毁，不影响原始 root。
错误 2 修复：位运算优先级
cpp 复制代码 
// 你的错误写法（优先级错）
return (1 << (leftHeight + 1) - 1 ) ; 
// 实际计算：1 << (leftHeight + 1 - 1) = 1 << leftHeight

// 正确写法（加括号保证先算位运算，再减1）
return (1 << (leftHeight + 1)) - 1; 
// 比如leftHeight=2，先算1<<3=8，再减1=7（正确的满二叉树节点数）
  • C++ 运算符优先级：-（减法）> <<（位左移），所以必须给 1 << (leftHeight + 1) 加括号，否则计算顺序错误。

测试验证（以示例 1 为例）

示例 1：root = [1,2,3,4,5,6]

  1. 计算左高度：root->left=2 → leftNode=2→4，leftHeight=2；
  2. 计算右高度：root->right=3 → rightNode=3→null，rightHeight=1；
  3. leftHeight≠rightHeight，递归计算：
    • 1 + countNodes(2) + countNodes(3)；
    • countNodes (2)：左高度 = 1（2→4），右高度 = 0（2→5→null），递归得 1+countNodes (4)+countNodes (5)=1+1+1=3；
    • countNodes (3)：左高度 = 0（3→6），右高度 = 0（3→null），满二叉树，返回 (1<<1)-1=1；
    • 总和：1+3+2=6（正确）。

错误：

  1. 核心错误 1：不要修改递归的原始入参（root），计算高度时必须用临时变量遍历；
  2. 核心错误 2：位运算和算术运算混合时，注意优先级，加括号保证计算顺序；
  3. 递归关键：递归过程中，原始根节点必须保持不变，否则后续递归的入参全错。

终于通过了

cpp 复制代码 
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        if (root == nullptr){
            return 0 ;
        }
        int leftHeight = 0 ; 
        TreeNode* leftNode = root -> left ;
        while (leftNode != nullptr){
            leftHeight ++ ;
            leftNode = leftNode -> left ;
        }

        int rightHeight = 0 ;
        TreeNode* rightNode = root -> right ;
        while(rightNode != nullptr){
            rightHeight ++ ;
            rightNode = rightNode ->right ;
        }

        if (leftHeight == rightHeight ){
            return (1 << (leftHeight + 1) ) - 1  ;
        }
        return 1 + countNodes(root -> left ) + countNodes(root -> right);
    }
};

5 小结

见多识广，知道这个解法就算是暴力也应该做出来。多积累，多反思。补充一下位运算，还有dfs的实现，其实大可以自己private一个函数function再左，要是看题目里面只给一个参数确实不好写。思路都有，怎么就是写不来代码，不知道怎么去提升。其实也许拿来背诵也该记住，写多了就有记忆了？

召唤ai老师...

一、核心知识点总结（两道题通用 + 专属）

1. 深度优先搜索（DFS）核心逻辑（通用）

DFS 解决二叉树问题的本质是分解问题 + 明确终止条件，所有递归写法都遵循这个模板：

cpp 复制代码 
// 通用DFS模板（二叉树）
返回值 dfs(当前节点, 状态参数) {
    // 1. 终止条件：空节点/叶子节点（根据题目定）
    if (节点为空) return 基准值;
    
    // 2. 处理当前节点：更新状态（比如累积数字/统计高度）
    状态更新逻辑;
    
    // 3. 递归处理左右子树：合并结果
    return 左子树递归结果 + 右子树递归结果;
}
  • 129 题：状态参数是curSum（累积数字），终止条件是 "空节点返回 0，叶子节点返回 curSum"；
  • 222 题：暴力版无额外状态，终止条件是 "空节点返回 0"；进阶版状态是 "左右高度"，终止条件新增 "满二叉树直接返回公式结果"。
2. 129. 求根到叶数字之和（专属要点）
  • 核心技巧：数值累加 curSum * 10 + node->val，避免字符串转换（高效）；
  • 关键：递归时curSum是 "值传递"，每层递归的curSum独立，不会互相干扰；
  • 备选思路：字符串拼接（直观但效率低），适合理解路径遍历逻辑。
3. 222. 完全二叉树节点数（专属要点）
版本 时间复杂度 核心逻辑 关键注意点
暴力 DFS O(n) 1 + 左子树节点数 + 右子树节点数 终止条件先写（空节点返回 0）
进阶优化 O(log²n) 利用满二叉树特性减少递归 ① 用临时变量算高度，不修改 root；② 位运算加括号保证优先级
  • 满二叉树公式：(1 << (高度+1)) - 1（1 << n等价于2^n，位运算更快）；
  • 高度计算：左高度 = 一直往左走的步数，右高度 = 一直往右走的步数，相等则为满二叉树。

二、高频踩坑点（你亲身遇到的）

  1. 修改原始入参 ：计算高度时直接改root，导致后续递归入参错误（必须用临时变量leftNode/rightNode）；
  2. 运算符优先级 ：位运算<<优先级低于减法-，必须给1 << (h+1)加括号；
  3. 终止条件缺失 / 写错：递归先想 "什么时候停"，再想 "怎么算"，空节点返回 0 是二叉树递归的基础；
  4. 思路到代码的断层：知道 "用高度判断满二叉树"，但不知道 "用临时变量遍历算高度"，本质是 "把抽象思路拆成具体代码步骤" 的能力不足。

三、提升代码落地能力的方法（针对性解决 "思路有但写不出"）

  1. 先 "抄" 后 "改"，再 "写" ：
    • 第一步：抄通能运行的代码（比如暴力版），逐行注释含义，理解每一步的作用；
    • 第二步：改代码（比如给暴力版加高度计算），只改一小部分，运行验证是否正确；
    • 第三步：脱离参考，从头写，卡壳时只看 "核心思路"，不看完整代码。
  2. 模板化记忆，而非死记代码 ：
    • 记住 DFS 的 "终止条件→处理当前节点→递归左右子树" 三步模板，不管题目怎么变，套模板填逻辑；
    • 比如遇到新的二叉树题，先写if (root == nullptr) return 0;，再想当前节点该处理什么。
  3. 刻意练 "拆步骤" ：
    • 拿到思路（比如 "算高度判断满二叉树"），先拆成代码小步骤：① 定义临时变量leftNode = root->left；② 循环遍历算 leftHeight；③ 同理算 rightHeight；④ 判断相等则用公式；
    • 把抽象思路拆成 "能写出来的代码行"，是新手到熟手的关键。
  4. 积累 "小技巧" ：
    • 二叉树递归中，原始入参（如root）尽量不修改，用临时变量操作；
    • 位运算替代幂运算（1 << n代替pow(2, n)），既快又避免浮点误差；
    • 私有函数（private）拆分逻辑（比如 129 题把 DFS 写成私有函数），适配题目给定的函数参数。

四、最终小结

  1. 二叉树 DFS 的核心是 "终止条件 + 分解子问题"，先保证暴力版能写出来，再谈优化；
  2. 思路到代码的落地，关键是把 "抽象思路拆成具体代码步骤"，比如 "算高度" 拆成 "定义临时变量→循环遍历→计数"；
  3. 踩坑不可怕，每解决一个坑（比如改 root、运算符优先级），就是一次实打实的进步，记下来这些坑，下次遇到直接规避。

你现在已经能从 "写不出" 到 "踩坑后能改对"，这是最关键的突破！接下来可以找同类二叉树 DFS 题（比如路径总和、二叉树的所有路径），用同样的方法练，写多了模板会刻在脑子里，思路到代码的转化会越来越快。

相关推荐
1027lonikitave1 小时前
FFTW的expr.ml怎么起作用
算法·哈希算法
TracyCoder1231 小时前
LeetCode Hot100（54/100）——215. 数组中的第K个最大元素
算法·leetcode·排序算法
We་ct1 小时前
LeetCode 92. 反转链表II ：题解与思路解析
前端·算法·leetcode·链表·typescript
阿i索1 小时前
流对象输入输出（cin/cout）
c++·笔记·学习
载数而行5201 小时前
数据结构系列15之图的存储方式2
c语言·数据结构·c++
春日见1 小时前
如何查看我一共commit了多少个，是哪几个，如何回退到某一个版本
vscode·算法·docker·容器·自动驾驶
uesowys2 小时前
华为OD算法开发指导-二级索引-Read and Write Path Different Version
java·算法·华为od
TracyCoder1232 小时前
LeetCode Hot100（55/100）——347. 前 K 个高频元素
数据结构·算法·leetcode
码农三叔2 小时前
（11-4-03）完整人形机器人的设计与实现案例：盲踩障碍物
人工智能·算法·机器人·人机交互·人形机器人
热门推荐
01GitHub 镜像站点02Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services03爬虫逆向之观安（观镜WEB应用安全防护系统）04openClaw安装飞书插件｜核心踩坑：spawn EINVAL 错误终极解决指南05BongoCat - 跨平台键盘猫动画工具06HTB 赛季10 - Pterodactyl - user07UV安装并设置国内源08243 行 microGPT：把“训练 + 推理”拆到骨头里09openclaw配置教程（linux+局域网ollama）10openclaw 配置飞书 报错 应用未建立长连接