MOEA/D（基于分解的多目标进化算法）求解46个多目标函数及一个工程应用，包含四种评价指标，MATLAB代码

基于分解的多目标进化算法（Multi‑Objective Evolutionary Algorithm Based on Decomposition, MOEA/D）是2007年首次提出一种多目标算法，是多目标进化优化领域的里程碑式框架。其核心范式是将原始多目标优化问题（MOP）通过标量化函数分解为一组单目标子问题，依托子问题间的邻域协作机制并行优化，最终以子问题最优解的集合逼近原问题的帕累托最优前沿（Pareto Front, PF）。该框架突破了传统基于帕累托支配的进化算法在高维目标空间中选择压力衰减、计算复杂度激增的瓶颈，成为当前多目标进化算法的主流分支之一。

一、理论基础与问题定义

1.1 多目标优化问题（MOP）数学表述

无约束MOP的标准形式为：
min⁡F(x)=(f1(x),f2(x),...,fM(x))Ts.t.x∈Ω \begin{align*} \min \quad & \mathbf{F}(\mathbf{x}) = \left(f_1(\mathbf{x}), f_2(\mathbf{x}), \dots, f_M(\mathbf{x})\right)^T \\ \text{s.t.} \quad & \mathbf{x} \in \Omega \end{align*} mins.t.F(x)=(f1(x),f2(x),...,fM(x))Tx∈Ω

其中：

x=(x1,x2,...,xN)T\mathbf{x} = (x_1, x_2, \dots, x_N)^Tx=(x1,x2,...,xN)T 为决策向量，Ω⊆RN\Omega \subseteq \mathbb{R}^NΩ⊆RN 为N维决策空间；
F(x)\mathbf{F}(\mathbf{x})F(x) 为M维目标向量 ，fi:Ω→Rf_i: \Omega \to \mathbb{R}fi:Ω→R 为第iii个目标函数；
M≥2M \ge 2M≥2 为目标维度，各目标通常相互冲突，不存在使所有目标同时最优的单一解。

1.2 帕累托最优核心概念

帕累托支配 ：解x1\mathbf{x}^1x1 支配x2\mathbf{x}^2x2（记为x1≺x2\mathbf{x}^1 \prec \mathbf{x}^2x1≺x2），当且仅当∀i∈{1,...,M},fi(x1)≤fi(x2)\forall i \in \{1, \dots, M\}, f_i(\mathbf{x}^1) \le f_i(\mathbf{x}^2)∀i∈{1,...,M},fi(x1)≤fi(x2) 且 ∃j∈{1,...,M},fj(x1)<fj(x2)\exists j \in \{1, \dots, M\}, f_j(\mathbf{x}^1) < f_j(\mathbf{x}^2)∃j∈{1,...,M},fj(x1)<fj(x2)。
帕累托最优解 ：若x∗∈Ω\mathbf{x}^* \in \Omegax∗∈Ω 不被任何其他解支配，则x∗\mathbf{x}^*x∗ 为帕累托最优解；所有帕累托最优解构成帕累托最优集（PS） ，其在目标空间的映射为帕累托最优前沿（PF）。

1.3 分解策略的数学本质

MOEA/D的核心是通过标量化聚合函数 将MOP转化为单目标子问题。设权重向量λ=(λ1,λ2,...,λM)T\boldsymbol{\lambda} = (\lambda_1, \lambda_2, \dots, \lambda_M)^Tλ=(λ1,λ2,...,λM)T 满足λi≥0\lambda_i \ge 0λi≥0 且∑i=1Mλi=1\sum_{i=1}^M \lambda_i = 1∑i=1Mλi=1（或∥λ∥1=1\|\boldsymbol{\lambda}\|1=1∥λ∥1=1），z∗=(z1∗,z2∗,...,zM∗)T\mathbf{z}^* = (z_1^*, z_2^*, \dots, z_M^*)^Tz∗=(z1∗,z2∗,...,zM∗)T 为理想点 （zi∗=min⁡x∈Ωfi(x)z_i^* = \min{\mathbf{x} \in \Omega} f_i(\mathbf{x})zi∗=minx∈Ωfi(x)），常用标量化函数如下：

切比雪夫（Tchebycheff）标量化（最常用）
gte(x∣λ,z∗)=max⁡1≤i≤M{λi⋅∣fi(x)−zi∗∣}g^{\text{te}}(\mathbf{x} \mid \boldsymbol{\lambda}, \mathbf{z}^*) = \max_{1 \le i \le M} \left\{ \lambda_i \cdot \left| f_i(\mathbf{x}) - z_i^* \right| \right\}gte(x∣λ,z∗)=1≤i≤Mmax{λi⋅∣fi(x)−zi∗∣}

该函数对PF的非凸、凹形具有良好适应性，通过最大化加权偏差实现对特定权重方向的优化。
加权和（Weighted Sum）标量化
gws(x∣λ)=∑i=1Mλifi(x)g^{\text{ws}}(\mathbf{x} \mid \boldsymbol{\lambda}) = \sum_{i=1}^M \lambda_i f_i(\mathbf{x})gws(x∣λ)=i=1∑Mλifi(x)

仅适用于凸PF，非凸PF下会丢失大量最优解。
边界交叉（Boundary Intersection, BI）标量化
gbi(x∣λ,z∗)=θ∑i=1Mλi(fi(x)−zi∗)−min⁡1≤i≤M{fi(x)−zi∗}g^{\text{bi}}(\mathbf{x} \mid \boldsymbol{\lambda}, \mathbf{z}^*) = \theta \sum_{i=1}^M \lambda_i (f_i(\mathbf{x}) - z_i^*) - \min_{1 \le i \le M} \left\{ f_i(\mathbf{x}) - z_i^* \right\}gbi(x∣λ,z∗)=θi=1∑Mλi(fi(x)−zi∗)−1≤i≤Mmin{fi(x)−zi∗}

通过平衡收敛项与边界项，适配复杂PF形状。

二、MOEA/D核心框架与算法流程

2.1 核心设计思想

问题分解 ：生成一组均匀分布的权重向量{λ1,λ2,...,λN}\{\boldsymbol{\lambda}^1, \boldsymbol{\lambda}^2, \dots, \boldsymbol{\lambda}^N\}{λ1,λ2,...,λN}，将原MOP分解为NNN个单目标子问题，每个子问题对应一个权重向量与一个候选解。
邻域协作：基于权重向量的欧氏距离/夹角定义子问题邻域，进化操作（交叉、变异）仅在邻域内执行，实现局部信息共享与协同进化。
并行优化：所有子问题同步进化，通过邻域内的解替换机制，在提升收敛性的同时维持解集在目标空间的均匀分布。

2.2 标准MOEA/D算法步骤

步骤1：初始化

参数设置 ：设定种群规模NNN、邻域规模TTT、交叉概率pcp_cpc、变异概率pmp_mpm、最大迭代次数GmaxG_{\text{max}}Gmax。
权重向量生成 ：采用均匀设计、LHS（拉丁超立方抽样）或单纯格点法生成NNN个均匀分布的权重向量{λj}j=1N\{\boldsymbol{\lambda}^j\}_{j=1}^N{λj}j=1N。
邻域构建 ：对每个权重向量λj\boldsymbol{\lambda}^jλj，计算其与其他权重向量的欧氏距离，选取距离最近的TTT个向量，构成邻域索引集B(j)={j1,j2,...,jT}B(j) = \{j_1, j_2, \dots, j_T\}B(j)={j1,j2,...,jT}。
种群初始化 ：随机生成初始种群{xj}j=1N\{\mathbf{x}^j\}_{j=1}^N{xj}j=1N，xj\mathbf{x}^jxj 为子问题jjj的当前解；计算初始目标向量F(xj)\mathbf{F}(\mathbf{x}^j)F(xj)。
理想点初始化 ：zi∗=min⁡{fi(x1),fi(x2),...,fi(xN)},∀i=1,...,Mz_i^* = \min\{f_i(\mathbf{x}^1), f_i(\mathbf{x}^2), \dots, f_i(\mathbf{x}^N)\}, \forall i=1,\dots,Mzi∗=min{fi(x1),fi(x2),...,fi(xN)},∀i=1,...,M。

步骤2：进化操作（迭代执行）

父代选择 ：对当前子问题jjj，从其邻域B(j)B(j)B(j)中随机选取2个父代解xjp,xjq\mathbf{x}^{j_p}, \mathbf{x}^{j_q}xjp,xjq。
繁殖操作 ：对父代执行交叉（如模拟二进制交叉SBX）与变异（如多项式变异），生成子代解y\mathbf{y}y。
目标计算与理想点更新 ：计算F(y)\mathbf{F}(\mathbf{y})F(y)；若fi(y)<zi∗f_i(\mathbf{y}) < z_i^*fi(y)<zi∗，则更新zi∗=fi(y)z_i^* = f_i(\mathbf{y})zi∗=fi(y)。
邻域解更新（核心） ：对邻域B(j)B(j)B(j)内的每个子问题kkk：
- 计算子代y\mathbf{y}y 与当前解xk\mathbf{x}^kxk 的标量化函数值g(y∣λk,z∗)g(\mathbf{y} \mid \boldsymbol{\lambda}^k, \mathbf{z}^*)g(y∣λk,z∗) 与g(xk∣λk,z∗)g(\mathbf{x}^k \mid \boldsymbol{\lambda}^k, \mathbf{z}^*)g(xk∣λk,z∗)；
- 若g(y∣λk,z∗)<g(xk∣λk,z∗)g(\mathbf{y} \mid \boldsymbol{\lambda}^k, \mathbf{z}^*) < g(\mathbf{x}^k \mid \boldsymbol{\lambda}^k, \mathbf{z}^*)g(y∣λk,z∗)<g(xk∣λk,z∗)，则用y\mathbf{y}y 替换xk\mathbf{x}^kxk（xk=y\mathbf{x}^k = \mathbf{y}xk=y）。

步骤3：终止判断

若迭代次数达到GmaxG_{\text{max}}Gmax，则终止算法；输出种群{xj}j=1N\{\mathbf{x}^j\}_{j=1}^N{xj}j=1N 作为原MOP的帕累托最优解近似集。

三、关键技术模块解析

3.1 权重向量生成与分布

权重向量的分布直接决定最终解集的均匀性，主流方法包括：

单纯格点法 ：适用于低维目标（M≤3M \le 3M≤3），生成严格均匀的权重向量，但MMM增大时数量呈组合爆炸。
均匀设计/拉丁超立方：适用于高维目标，在保证空间填充性的同时控制向量数量。
自适应权重调整：根据进化过程中PF的形状动态调整权重分布，解决复杂PF（如凹、不连续）下的分布失衡问题。

3.2 邻域结构与协作机制

邻域定义 ：以权重向量的相似度为依据，将全局优化转化为局部邻域内的协作，大幅降低计算复杂度（从O(N2)O(N^2)O(N2)降至O(NT)O(NT)O(NT)，T≪NT \ll NT≪N）。
信息共享机制：邻域内子问题共享进化信息，使相近偏好方向的解相互促进，既保证局部收敛，又通过全局邻域拓扑维持整体多样性。

3.3 解替换策略

标准MOEA/D采用邻域内贪婪替换：子代仅在邻域内竞争，优于当前解则替换。该策略的优势在于：

避免全局非支配排序的高复杂度；
每个子问题独立优化，目标维度增加时选择压力不衰减；
天然适配并行计算架构，可高效部署于分布式系统。

四、MOEA/D的优势与局限性

4.1 核心优势

计算效率高：规避全局非支配排序，复杂度显著低于NSGA‑II、SPEA2等支配型算法，尤其适配高维目标优化（MaOPs）。
收敛‑分布平衡：通过权重向量与邻域协作，在快速收敛的同时维持解集在PF上的均匀分布。
框架灵活性强：可无缝集成各类标量化函数、进化算子与优化策略，易于扩展与改进。
理论基础扎实：标量化函数的最优解与原MOP的帕累托最优解存在严格对应关系，为算法收敛性分析提供理论支撑。

4.2 主要局限性

权重向量依赖：固定权重向量难以适配复杂、不规则PF（如凹形、不连续、退化），易导致解集分布失衡。
邻域参数敏感 ：邻域规模TTT需人工调参，过小易陷入局部最优，过大则丧失局部协作优势。
理想点动态性 ：理想点z∗\mathbf{z}^*z∗ 随进化更新，若更新滞后会导致标量化函数评估偏差，影响收敛。
高维目标挑战 ：当M>10M>10M>10时，权重向量均匀分布的难度激增，解集覆盖性与多样性难以保证。

五、MOEA/D应用

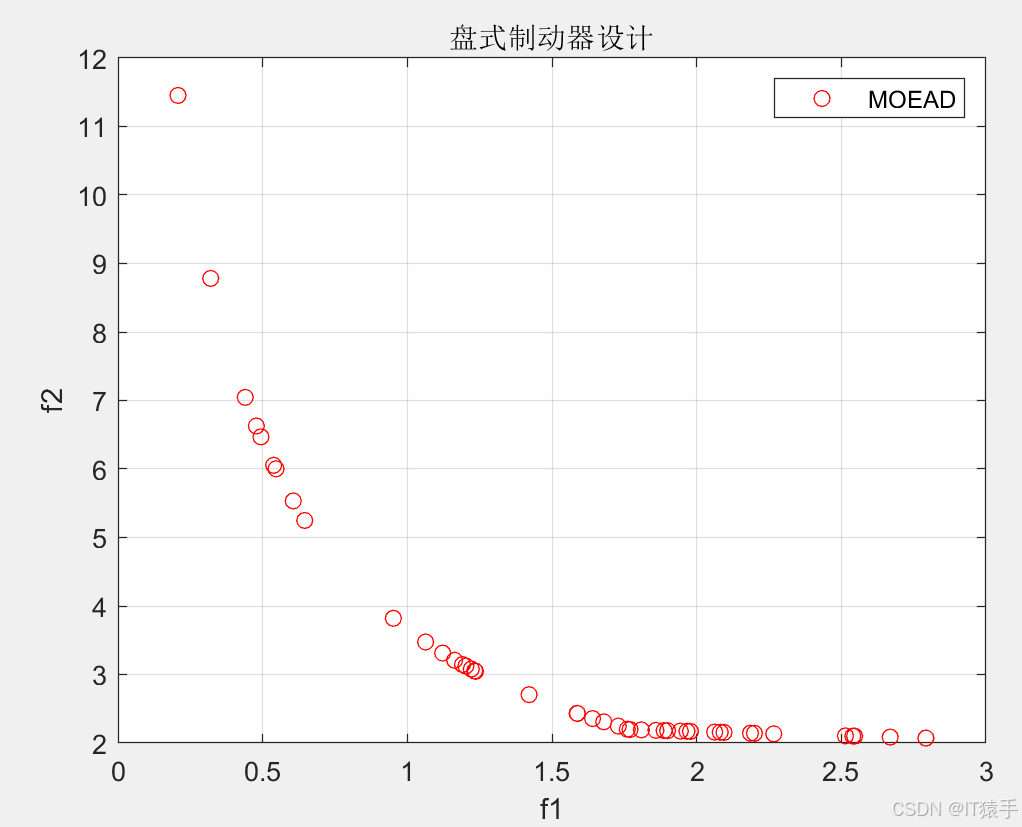
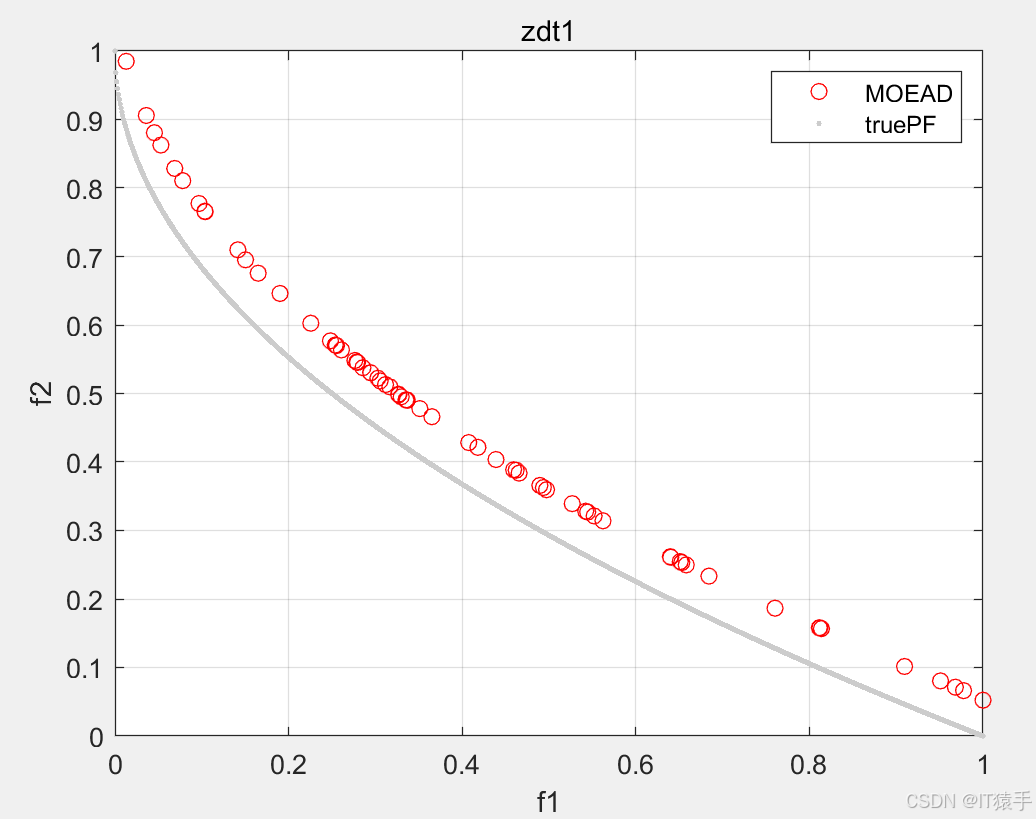
MOEA/D用于求解46个多目标测试函数（ZDT1、ZDT2、ZDT3、ZDT4、ZDT6、DTLZ1-DTLZ7、WFG1-WFG10、UF1-UF10、CF1-CF10、Kursawe、Poloni、Viennet2、Viennet3）以及1个工程应用（盘式制动器设计）,并采用IGD、GD、HV、SP进行评价。

1部分代码

bash 复制代码

close all;
clear ; 
clc;
%%
% TestProblem测试问题说明：
%一共46个多目标测试函数，详情如下：
%1-5:ZDT1、ZDT2、ZDT3、ZDT4、ZDT6
%6-12：DZDT1-DZDT7
%13-22：wfg1-wfg10
%23-32：uf1-uf10
%33-42：cf1-cf10
%43-46:Kursawe、Poloni、Viennet2、Viennet3
%47 盘式制动器设计 温泽宇,谢珺,谢刚,续欣莹.基于新型拥挤度距离的多目标麻雀搜索算法[J].计算机工程与应用,2021,57(22):102-109.
%%
TestProblem=47;%1-47
MultiObj = GetFunInfo(TestProblem);
MultiObjFnc=MultiObj.name;%问题名
% Parameters
params.Np = 100;        % Population size
params.Nr = 100;        % Repository size
params.maxgen =100;    % Maximum number of generations
[x,f] = MOEAD(params,MultiObj);