数据结构算法学习day3——二分查找

一.算法描述

二.算法实现

java 复制代码

package com.algorithm.binarysearch;

public class BinarySearch {
    /*params:a - 待查找的升序数组
             target - 待查找的目标值
      Returns：
            找到则返回索引
            找不到则返回-1
    * */
    public static int binarySearch(int[] a,int target){//设置元素个数数组和待查找的目标值
        int i = 0,j = a.length - 1;//设置指针和初值
        while(i<=j){
            int m = (i+j) >>> 1; //用无符号右移运算符，防止溢出
            if(target < a[m]){//目标值在中间值左边的情况下
                j = m - 1;
            }else if(target >a[m]){//目标值在中间值右边的情况下
                i = m + 1;
            }else {
                return m; //找到中间值
            }
        }
        return -1;//找不到的情况下返回-1
    }
}

java 复制代码

package com.algorithm.binarysearch;

public class BinarySearch {
    /*params:a - 待查找的升序数组
             target - 待查找的目标值
      Returns：
            找到则返回索引
            找不到则返回-1
    * */
    public static int binarySearch(int[] a,int target){//设置元素个数数组和待查找的目标值
        int i = 0,j = a.length;//设置指针和初值
        while(i<j){
            int m = (i+j) >>> 1; //用无符号右移运算符，防止溢出
            if(target < a[m]){//目标值在中间值左边的情况下
                j = m;
            }else if(target >a[m]){//目标值在中间值右边的情况下
                i = m + 1;
            }else {
                return m; //找到中间值
            }
        }
        return -1;//找不到的情况下返回-1
    }
}

三.查找问题

问题一

**q：**为什么是i<=j意味着区间内有未比较元素，而不是i<j?

**s:**i，j 它们指向的元素也会参与比较。

问题二

q:（i+j）/2有没有问题？

**s:**同一个二进制数，在java中会把第一位看作符号位，所以用">>>"无符号右移运算符，防止溢出。

问题三

**q:**在比较中写成"<"小于符号有何好处？

**s:**数组是升序排列的，写成小于符号可以是和数组升序排列方向一致，不然会很别扭。

四.如何判断算法好坏

1.时间复杂度

含义：是用来衡量一个算法的执行，随数据规模增大，而增长的时间成本。

2.如何表示时间复杂度

假设算法要处理的数据规模是n，代码总的执行行数用函数f（n）来表示，例如:

线性查找算法的函数f(n) = 3*n+3
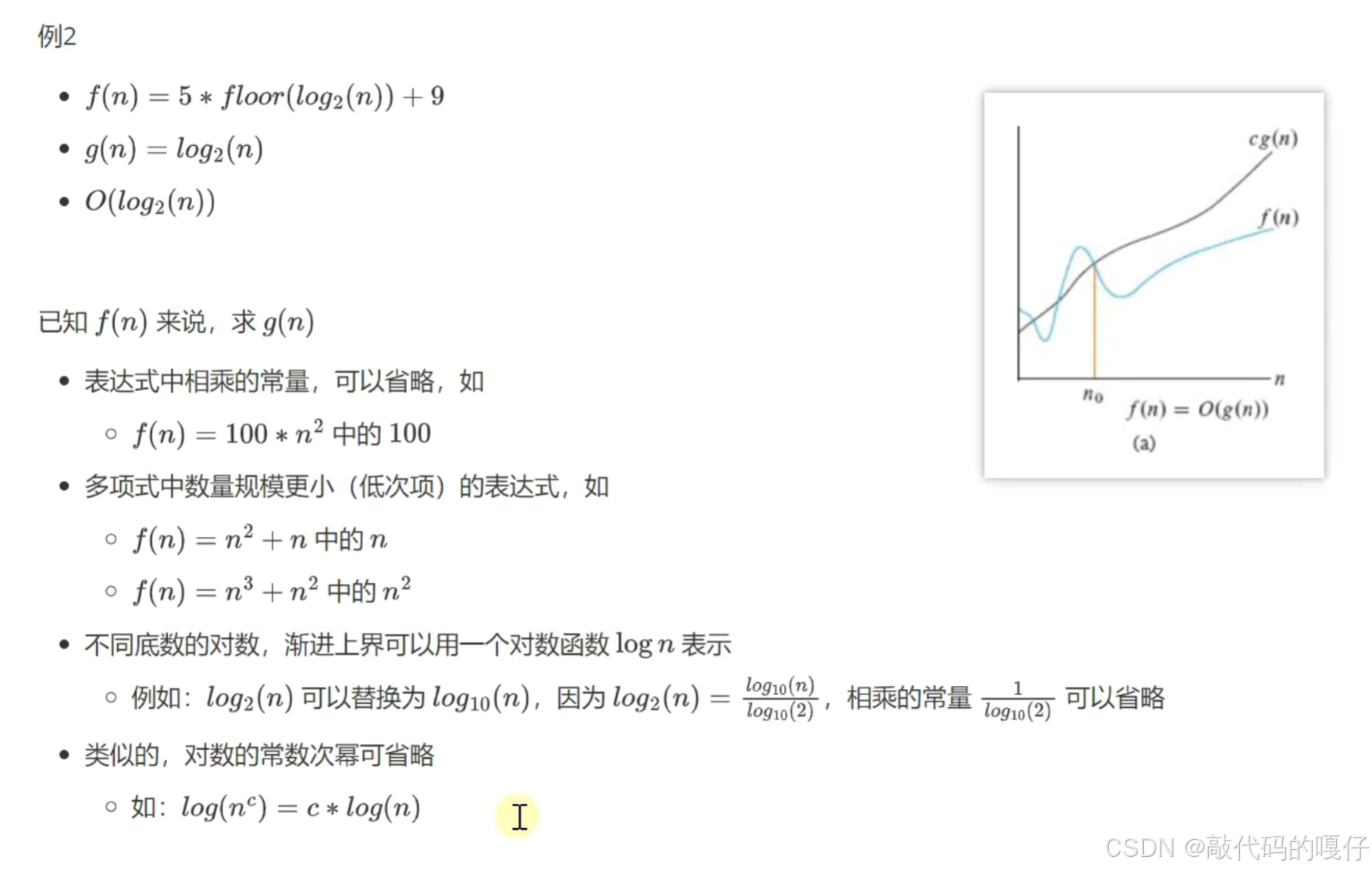
二分查找算法的函数f(n) = (floor(log2(n)+1)*5+4

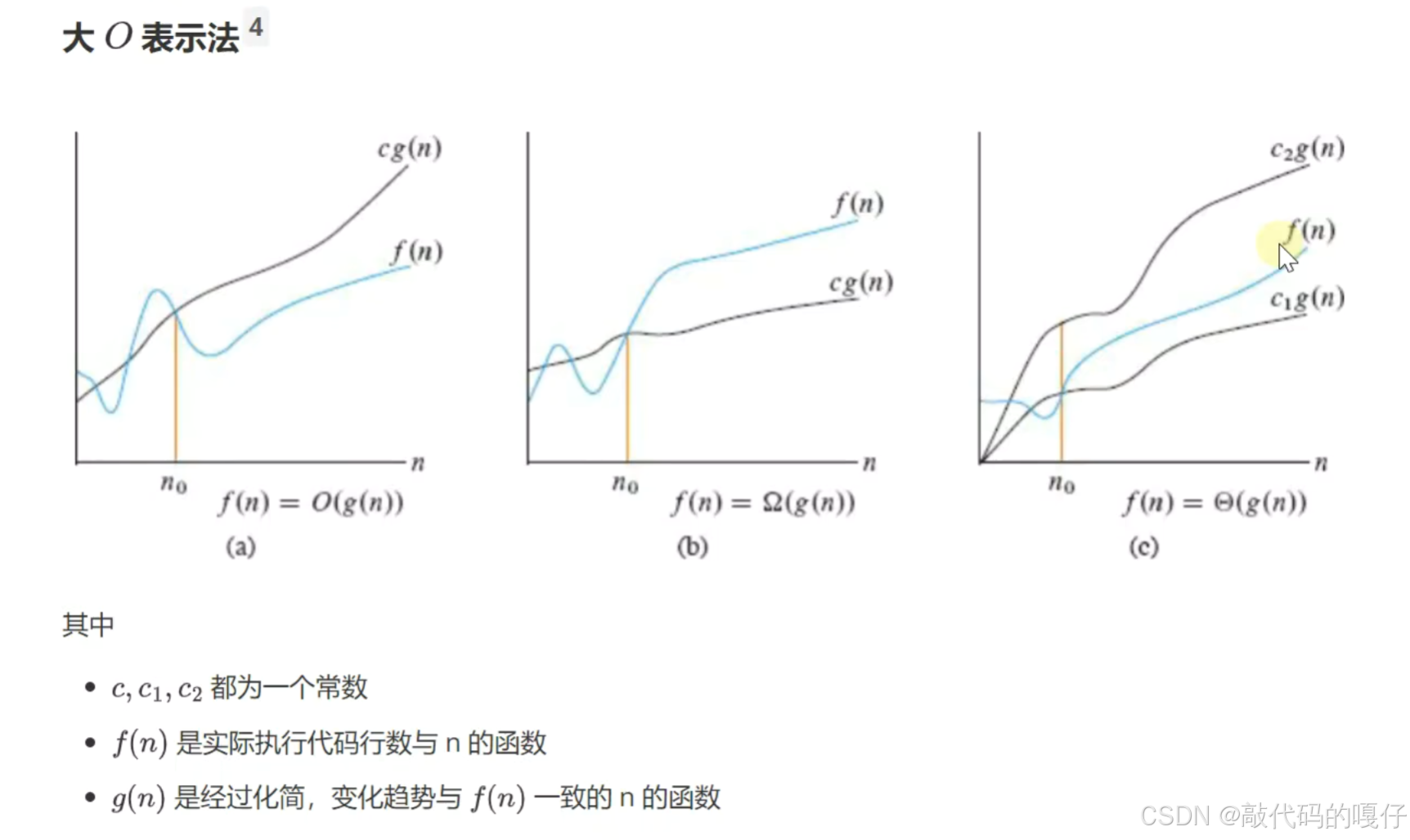
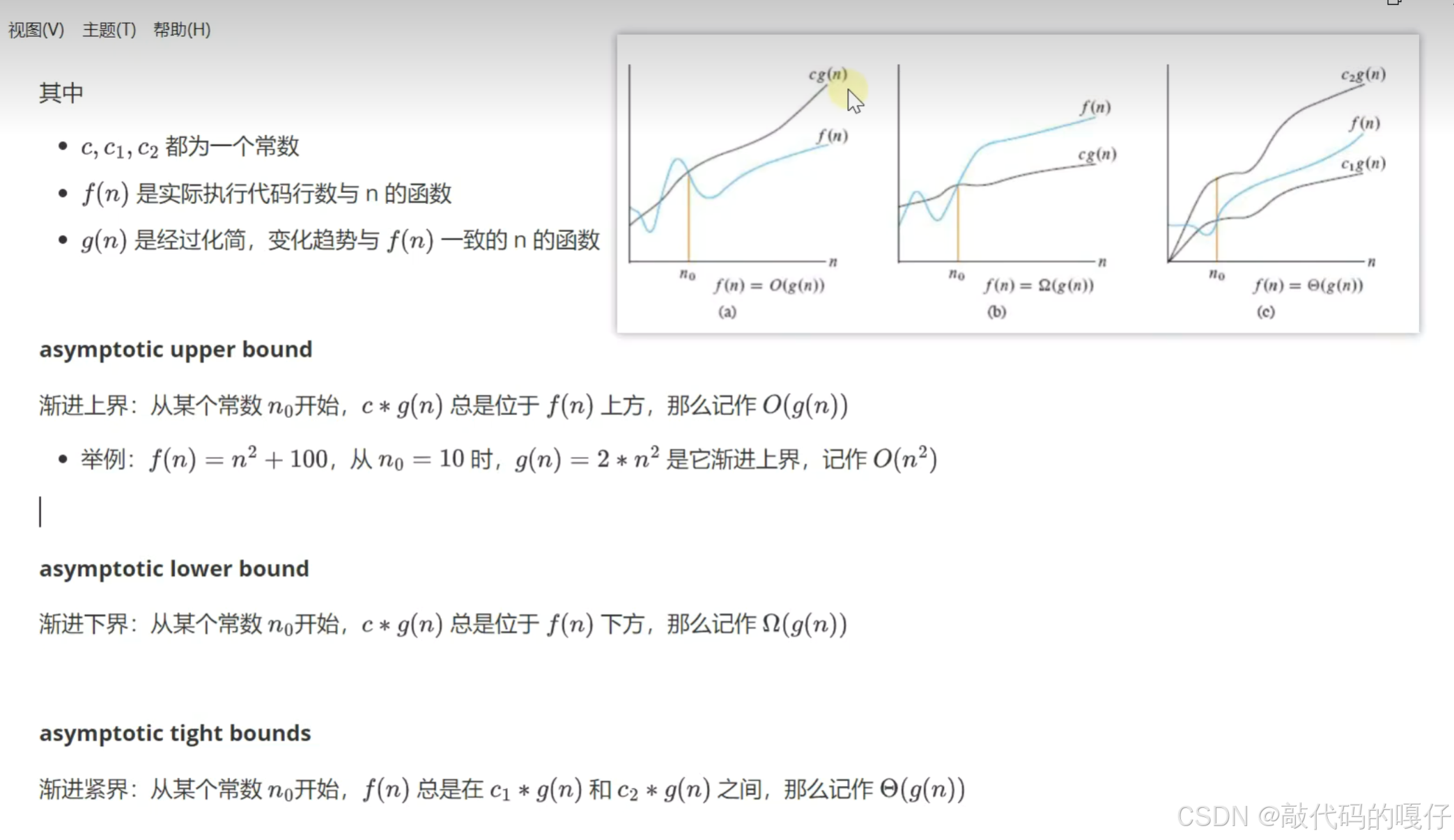
渐进上界：代表算法执行的最差情况

渐进下界：代表算法执行的最好情况

渐进紧界：既能代表算法执行的最好情况，也能代表算法执行的最差情况

3.常见的大O表示法

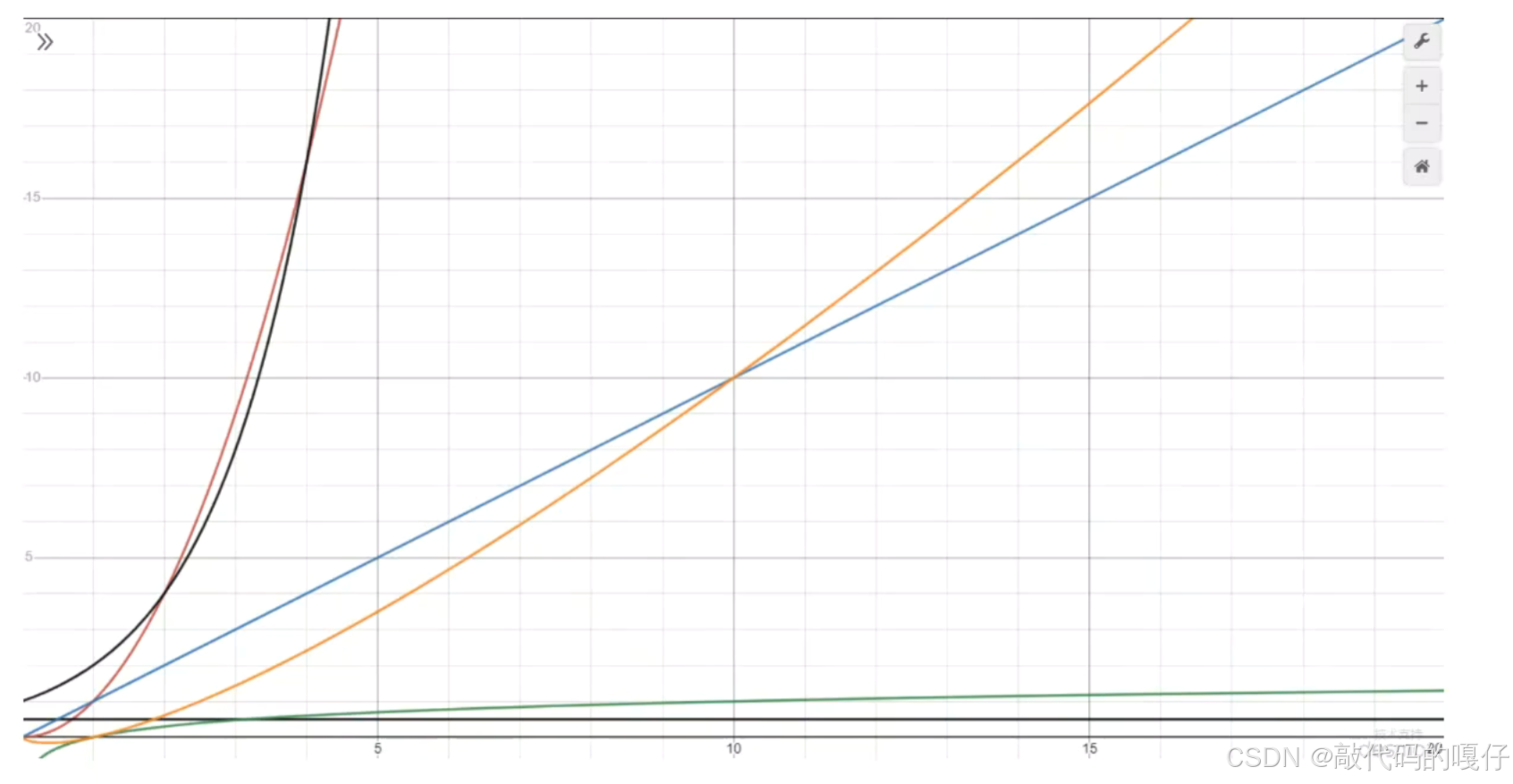
4.空间复杂度

与时间复杂度类似，一般也是用大O表示法来衡量：一个算法执行随数据规模增大，而增长的额外空间成本。

5.二分查找性能

五.插入数组

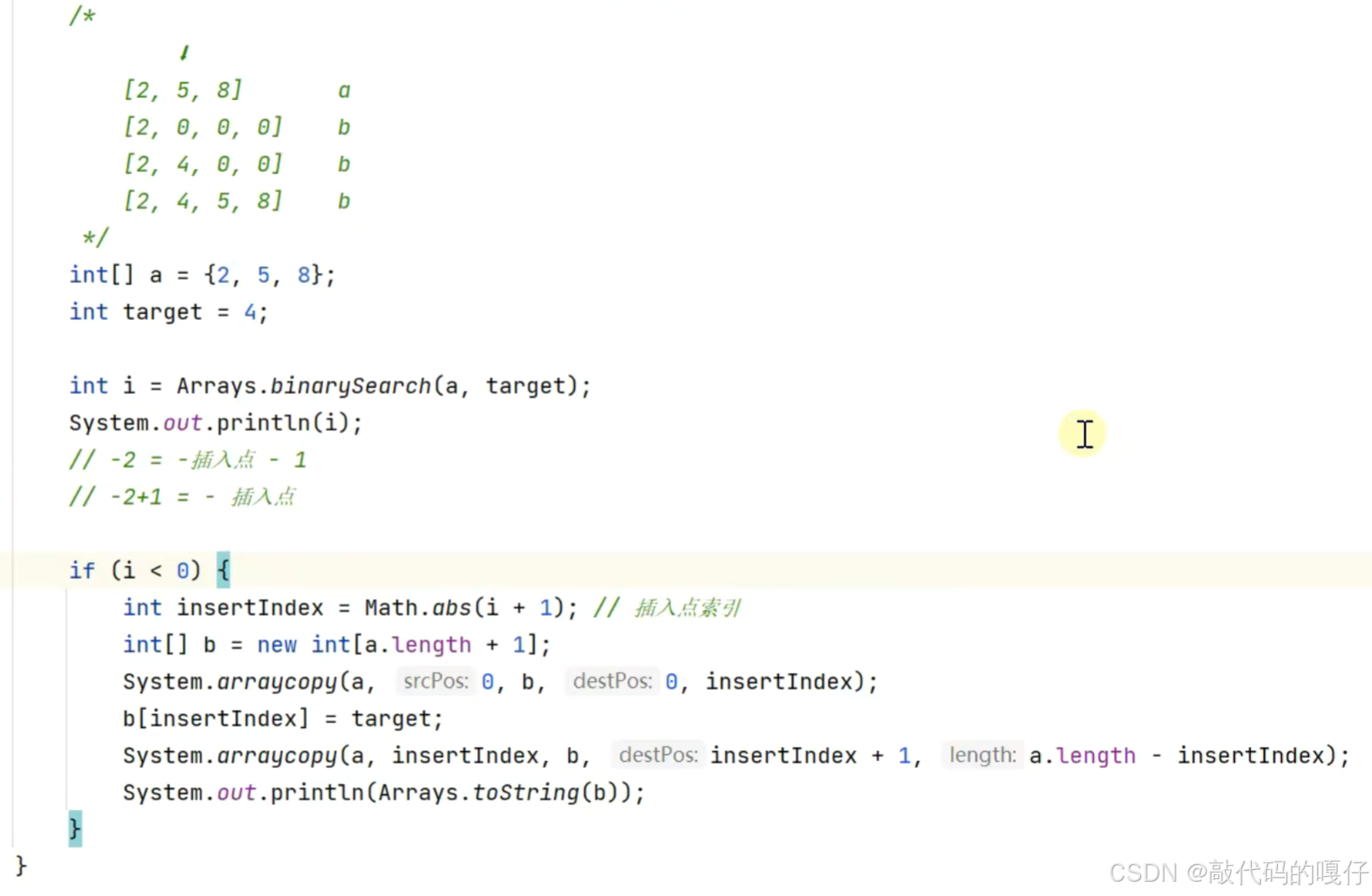
将数组中没有的元素插入进去

六.寻找最侧边元素

1.寻找最左侧元素

java 复制代码

package com.algorithm.binarysearch;

public class BinarySearch {
    /*params:a - 待查找的升序数组
             target - 待查找的目标值
      Returns：
            找到则返回索引
            找不到则返回-1
    * */
    public static int binarySearch(int[] a,int target){
        int i = 0,j = a.length - 1;
        int candidate = -1//表示没有任何候选者
        while(i<=j){
            int m = (i+j) >>> 1; 
            if(target < a[m]){
                j = m - 1;
            }else if(target >a[m]){
                i = m + 1;
            }else {
                //记录侯选位置
                condidate = m;
                j = m - 1;
            }
        }
        return -1;
}

2.寻找最右侧元素

java 复制代码

package com.algorithm.binarysearch;

public class BinarySearch {
    /*params:a - 待查找的升序数组
             target - 待查找的目标值
      Returns：
            找到则返回索引
            找不到则返回-1
    * */
    public static int binarySearch(int[] a,int target){
        int i = 0,j = a.length - 1;
        int candidate = -1//表示没有任何候选者
        while(i<=j){
            int m = (i+j) >>> 1; 
            if(target < a[m]){
                j = m - 1;
            }else if(target >a[m]){
                i = m + 1;
            }else {
                //记录侯选位置
                condidate = m;
                i = m + 1;
            }
        }
        return condidate;
}