数据结构——五十九、冒泡排序(王道408)

文章目录

• 前言
• 一.思路
• 二.具体例子
• 三.代码实现
• 四.算法性能分析
• • 1.空间复杂度
  • 2.时间复杂度
  • 3.稳定性
  • 4.适用性
• 五.知识回顾与重要考点
• 结语

前言

本文介绍了冒泡排序算法的基本思路、具体实现和性能分析。冒泡排序通过相邻元素比较交换实现排序，每趟将最小（或最大）元素"冒"到序列前端。算法采用双重循环实现，空间复杂度O(1)，最好时间复杂度O(n)，最坏和平均时间复杂度O(n²)。该算法稳定，既适用于顺序表也适用于链表。文章通过图示详细演示了排序过程，并给出了C语言实现代码，最后总结了算法特点和重要考点。
基于"交换"的排序：根据序列中两个元素关键字的比较结果来对换这两个记录在序列中的位置

一.思路

• 从后往前（或从前往后）两两比较相邻元素的值，若为逆序（即 A [ i − 1 ] > A [ i ] A[i-1]>A[i] A[i−1]>A[i]），则交换它们，直到序列比较完。称这样过程为"一趟"冒泡排序。
• 每做完一趟冒泡排序,需要注意的是,下一趟冒泡排序时前边已经确定最终位置的元素不用再对比
• 若某一趟排序没有发生"交换"，说明此时已经整体有序,无需往下对比

二.具体例子

• 目标:递增
  

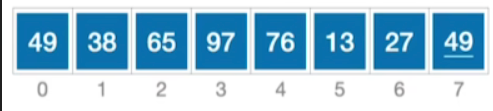
1. 先对比最后的这两个元素之间的大小关系,27<49,因此不交换
   
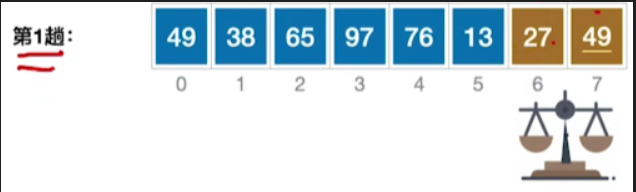
2. 接下来我们检查再往前的两个元素,13<27,不交换
   
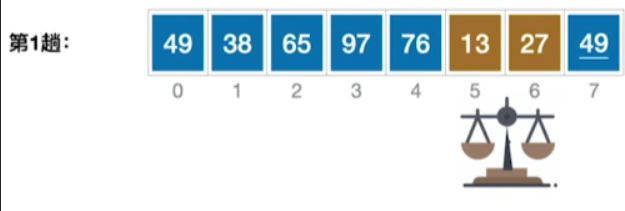
3. 接下来再往前链两个元素,76>13,交换
   
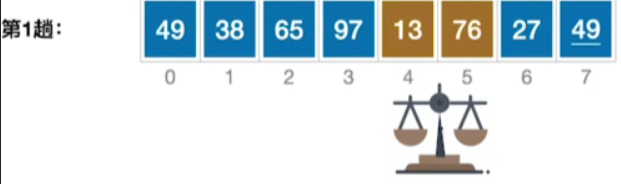
4. 后面也是一样的,无需做多赘述,直接看最终结果
   
5. 第一趟排序使关键字值最小的一个元素"冒"到最前面
   
6. 第二趟的处理也是一样,前边已经确定最终位置的元素不用再对比,这里是13
   
7. 第2趟结束后，最小的两个元素会"冒"到最前边
   
8. 接下来也不再赘述,原理和上面类似,值得注意的是,如果说两个元素的值相同的话,那么我们无需交换位置,这样可以保证算法的稳定性
   
9. 若某一趟排序没有发生"交换"，说明此时已经整体有序,无需往下对比
   

三.代码实现

//交换
void swap(int &a, int &b){
	int temp = a;
	a = b;
	b = temp;
}

//冒泡排序
void BubbleSort(int A[],int n){
	for(int i=0;i<n-1;i++){
		bool flag=false;	//表示本趟冒泡是否发生交换的标志
		for(int j=n-1;j>i;j--)	//一趟冒泡过程
			if(A[j-1]>A[j]){	//若为逆序
				swap(A[j-1],A[j]);	//交换
				flag=true;
			}
		if(flag==false)
			return;	//本趟遍历后没有发生交换，说明表已经有序
	}
}

• i所指位置之前的元素都已"有序",是作为一个界限存在的
• j为真正的工作指针,指向可能需要交换的元素
• 只有 A [ j − 1 ] > A [ j ] A[j-1]>A[j] A[j−1]>A[j]时才交换，因此算法是稳定的
• 用flag变量表示本次循环是否发生交换,若没有说明已经整体有序,退出循环

四.算法性能分析

1.空间复杂度

• O(1)

2.时间复杂度

• 最好情况
  

  • 比较次数=n-1；交换次数=0
  • 最好时间复杂度=O(n)

• 最坏情况
  

  • 比较次数 = ( n − 1 ) + ( n − 2 ) + ... + 1 = n ( n − 1 ) 2 = =(n-1)+(n-2)+\dotsc +1=\frac{n(n-1)}{2}= =(n−1)+(n−2)+...+1=2n(n−1)= 交换次数
  • 最坏时间复杂度 = O ( n 2 ) =\mathrm{O}(n^{2}) =O(n2)

• 平均时间复杂度=O(n²)

• 注意:每次交换 都需要移动元素3次

3.稳定性

• 稳定

4.适用性

• 冒泡排序是否适用于链表？
  
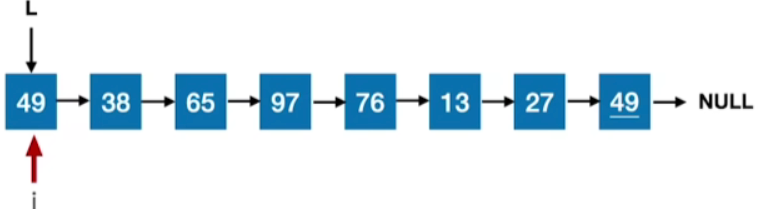
• 按照冒泡排序的思想,在上图中推演一遍,可从前往后"冒泡"，每一趟将更大的元素"冒"到链尾
  
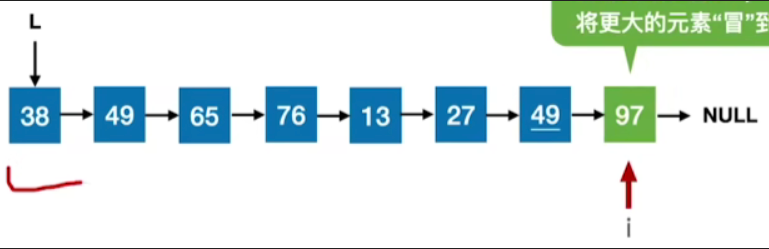
• 因此是可以的

五.知识回顾与重要考点

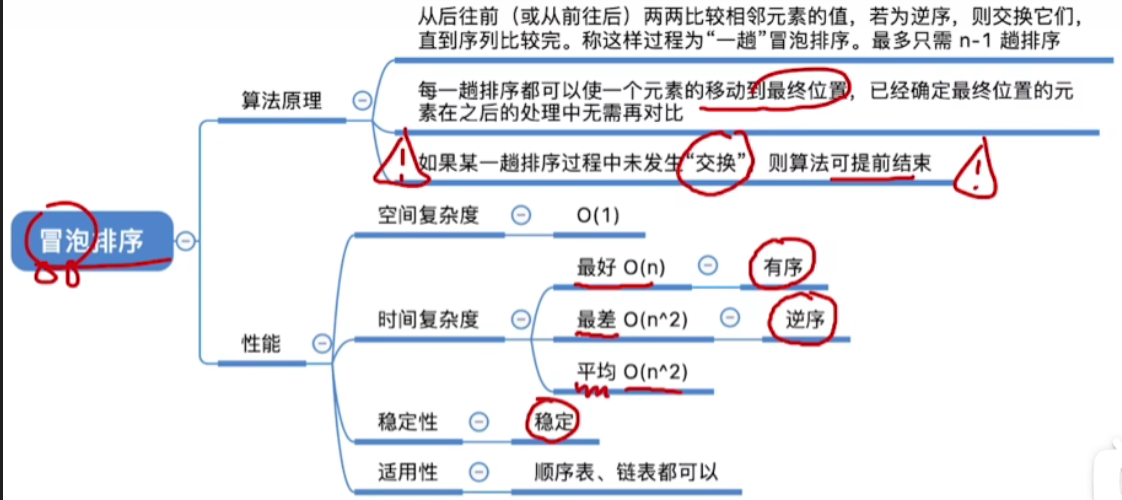
结语

七更😉
如果想查看更多章节,请点击:一、数据结构专栏导航页