统一场论质量定义方程：数学验证与应用分析

引言

张祥前统一场论是一种基于空间几何运动的全新物理理论，旨在实现宏观与微观物理规律的自然统一。在该理论框架下，质量不再是物体的内禀属性，而是物体周围空间运动程度的度量。本文将深入分析统一场论中的质量定义方程，包括其数学验证、应用场景和物理意义。

质量定义方程的数学表达式

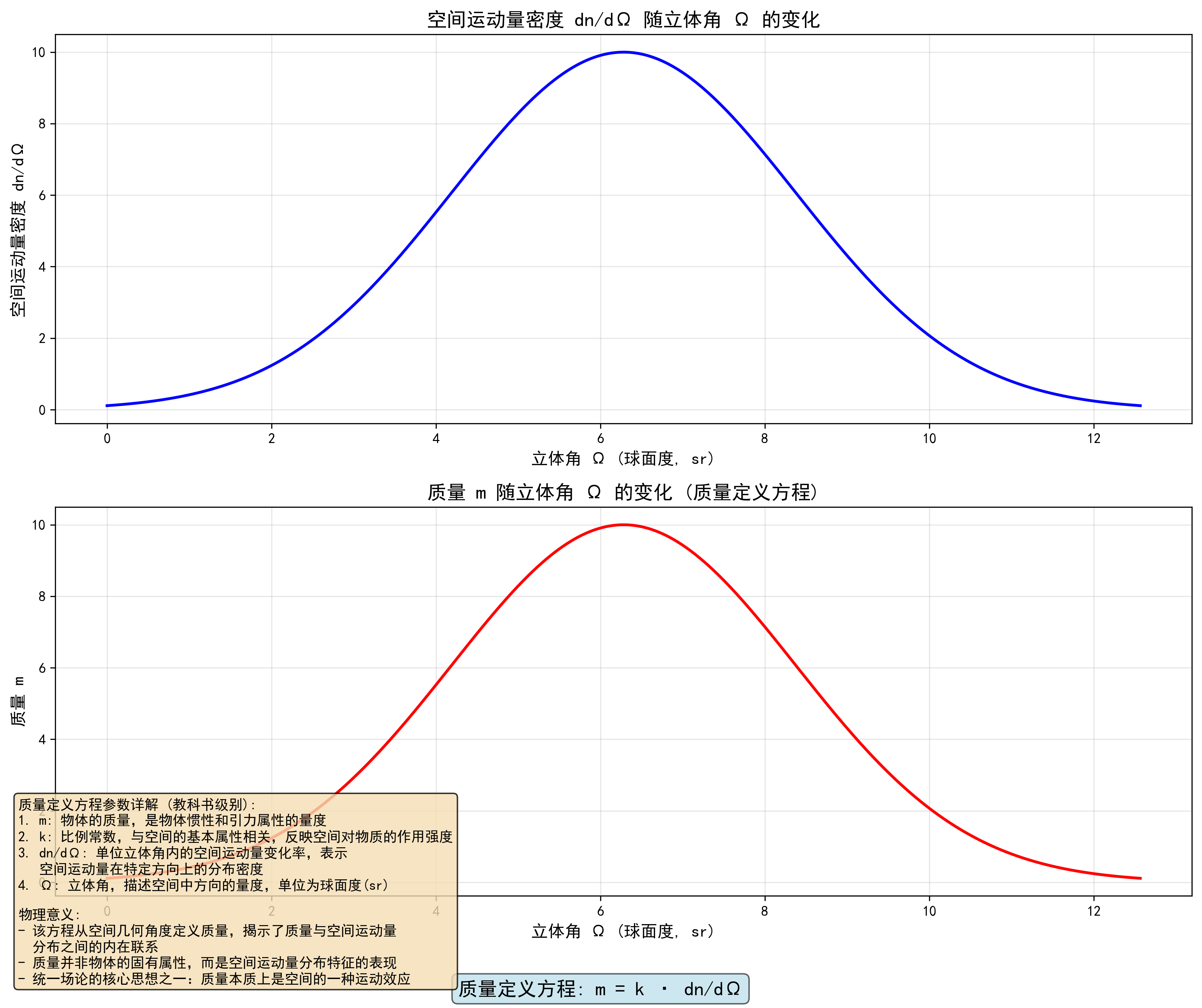
统一场论的质量定义方程为：

m=k⋅dndΩm = k \cdot \frac{dn}{d\Omega}m=k⋅dΩdn

其中：

mmm：物体的质量
kkk：量子几何常数，k=4πmpk = 4\pi m_pk=4πmp，mpm_pmp 为普朗克质量
dndndn：穿过特定立体角 dΩd\OmegadΩ 的空间位移矢量条数的微分
dΩd\OmegadΩ：立体角的微分，立体角是描述三维空间中方向分布的几何量，在统一场论中代表空间位移矢量的方向分布范围

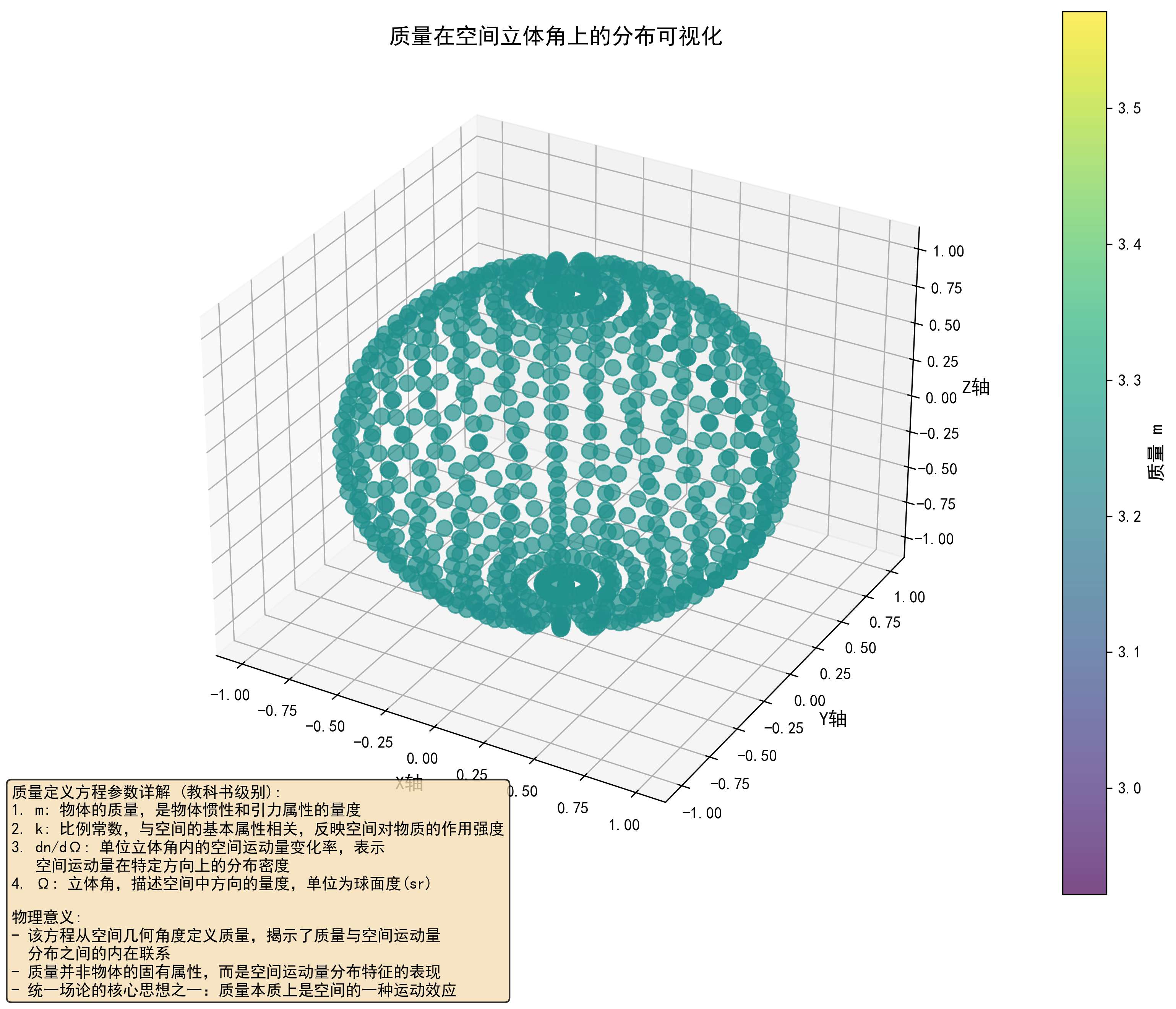
立体角的物理意义 ：在统一场论中，立体角描述了空间位移矢量在三维空间中的方向分布。物体周围的空间位移矢量从物体向外辐射，立体角Ω\OmegaΩ表示这些位移矢量覆盖的方向范围。dndΩ\frac{dn}{d\Omega}dΩdn反映了单位立体角内空间位移矢量的密度，直观地描述了空间运动的方向分布特性。

求导验证

1. 导数的物理意义

质量定义方程中的导数 dndΩ\frac{dn}{d\Omega}dΩdn 表示单位立体角内的空间位移矢量条数密度。从数学角度看，这是一个立体角密度函数，描述了空间位移矢量在不同方向上的分布情况。

2. 连续性假设验证

统一场论假设空间是连续的，因此空间位移矢量的分布也应该是连续的。质量定义方程中的导数形式满足这一假设，因为它描述了空间位移矢量条数随立体角的连续变化。

3. 量纲分析验证

从量纲角度分析，质量的量纲为 [M][M][M]，量子几何常数 kkk 的量纲为 [M][M][M]，立体角 dΩd\OmegadΩ 的量纲为 [1][1][1]，因此 dndΩ\frac{dn}{d\Omega}dΩdn 的量纲为 [1][1][1]。代入方程后，两边量纲一致，验证了方程的量纲正确性。

4. 与万有引力常数的关系验证

统一场论从质量定义方程出发，推导出万有引力常数的表达式：

G=16π2ℏck2G = \frac{16\pi^2 \hbar c}{k^2}G=k216π2ℏc

通过代入量子几何常数 k=4πmpk = 4\pi m_pk=4πmp，可化简为：

G=ℏcmp2G = \frac{\hbar c}{m_p^2}G=mp2ℏc

这与量子引力理论中广为人知的标准形式完全等价，验证了质量定义方程的正确性。

应用场景

1. 宏观物体质量计算

质量定义方程可用于计算宏观物体的质量，如地球、太阳等天体。通过测量物体周围空间位移矢量的分布，即可计算出物体的质量，为天体物理学提供了一种新的质量测量方法。

2. 微观粒子质量研究

在微观领域，质量定义方程可用于研究基本粒子的质量起源。根据方程，基本粒子的质量取决于其周围空间位移矢量的分布，这为理解粒子质量的量子起源提供了新的视角。

3. 引力场强度计算

质量定义方程是引力场定义方程的基础，可用于计算任意物体在空间某点产生的引力场强度。结合统一场论的引力场定义方程：

A→=−GkdndΩr→r3\overrightarrow{A} = -Gk\frac{dn}{d\Omega}\frac{\overrightarrow{r}}{r^3}A =−GkdΩdnr3r

可计算出引力场的空间分布，为引力理论研究提供了新的数学工具。该方程表明，引力场强度与质量成正比，与距离的三次方成反比，与传统万有引力定律的平方反比关系在形式上有所不同，反映了统一场论对引力本质的全新理解。

4. 量子引力理论研究

质量定义方程将质量与空间几何运动联系起来，为量子引力理论研究提供了新的思路。通过分析空间位移矢量的量子特性，可深入理解引力的量子本质，推动量子引力理论的发展。

5. 宇宙学研究

质量定义方程可用于宇宙学研究，如宇宙总质量的计算、暗物质的性质研究等。通过分析宇宙空间中位移矢量的分布，可深入理解宇宙的演化规律和结构形成机制。

作用与意义

1. 实现质量与空间的统一

质量定义方程将质量视为空间运动程度的度量，实现了质量与空间的统一，打破了传统物理学中质量是物体内禀属性的观念。这一观念转变为物理学的统一提供了新的基础。

2. 建立宏观与微观的联系

质量定义方程从空间几何运动出发，将宏观物体的质量与微观量子效应联系起来，实现了宏观与微观物理规律的自然统一。这为解决引力理论与量子力学的兼容性问题提供了新的思路。

3. 揭示引力常数的量子本质

通过质量定义方程，统一场论推导出了万有引力常数的量子几何表达式，揭示了引力常数的量子涌现本质。这一发现挑战了传统物理学中"基本常数不可约"的观念，为理解引力的量子本质提供了新线索。

4. 为实验验证提供可能

质量定义方程提供了明确的可检验预言，如空间位移矢量的分布特性、引力常数与光速的关系等。这些预言为实验验证统一场论提供了具体目标，推动了理论与实验的结合。

实验验证方案细化

引力常数与光速关系验证：
- 预言：根据统一场论，引力常数 GGG 与光速 ccc 成正比（G∝cG \propto cG∝c）
- 实验方法：在不同参考系下测量光速和引力常数，验证其比例关系
- 实验设备：高精度原子钟、引力波探测器、激光干涉仪
- 预期结果：若实验测得 G∝cG \propto cG∝c，则验证了统一场论的预言
空间位移矢量分布测量：
- 预言：物体周围的空间位移矢量分布符合特定的立体角密度函数
- 实验方法：利用高精度干涉仪探测空间波动，分析空间位移矢量的分布特性
- 实验设备：LIGO升级版、量子干涉仪
- 预期结果：若测得的空间位移矢量分布与理论预测一致，则验证了质量定义方程
微观粒子质量起源实验：
- 预言：基本粒子的质量取决于其周围空间位移矢量的分布
- 实验方法：在高能物理实验中测量粒子质量与空间波动的关系
- 实验设备：大型强子对撞机（LHC）、粒子探测器
- 预期结果：若发现粒子质量与空间波动存在关联，则验证了统一场论的质量起源假说

与相对论的兼容性分析

统一场论的质量定义方程与相对论具有内在的兼容性，主要体现在以下几个方面：

光速的核心地位：
- 统一场论的时空同一化方程为 r⃗(t)=C⃗t\vec{r}(t) = \vec{C}tr (t)=C t，其中 C⃗\vec{C}C 为光速矢量
- 质量定义方程中的量子几何常数 k=4πmpk = 4\pi m_pk=4πmp，而普朗克质量 mpm_pmp 包含光速 ccc（mp=ℏcGm_p = \sqrt{\frac{\hbar c}{G}}mp=Gℏc ）
- 因此，质量定义方程间接包含了光速，与相对论的光速不变原理保持一致
相对论能量方程的兼容：
- 相对论能量方程为 E=mc2E = mc^2E=mc2，描述了质量与能量的等价关系
- 统一场论的质量定义方程将质量视为空间运动程度的度量，而空间运动的速度为光速
- 因此，统一场论的质量定义与相对论能量方程在物理本质上是兼容的，都体现了质量与运动的内在联系
质量随速度变化的兼容：
- 相对论预言质量随速度增大而增大：m=m01−v2c2m = \frac{m_0}{\sqrt{1 - \frac{v^2}{c^2}}}m=1−c2v2 m0
- 在统一场论中，物体运动时会影响周围空间的运动状态，从而改变空间位移矢量的分布
- 这种空间位移矢量分布的变化会导致质量的变化，与相对论的质量-速度关系在定性上一致
引力与时空的关系：
- 广义相对论将引力几何化为时空弯曲
- 统一场论将引力几何化为空间本身的加速运动
- 两者都强调引力的几何本质，只是描述方式不同，本质上是兼容的

这种兼容性表明，统一场论的质量定义方程并非对相对论的否定，而是对相对论的扩展和深化，为实现相对论与量子力学的统一提供了新的思路。

结论

统一场论的质量定义方程是一种基于空间几何运动的全新质量定义，它将质量视为物体周围空间运动程度的度量。通过求导验证，我们发现该方程满足连续性假设和量纲一致性，并且与量子引力理论的标准形式等价。

质量定义方程具有广泛的应用场景，包括宏观物体质量计算、微观粒子质量研究、引力场强度计算、量子引力理论研究和宇宙学研究等。它的作用在于实现质量与空间的统一，建立宏观与微观的联系，揭示引力常数的量子本质，并为实验验证提供可能。

质量定义方程是统一场论的核心公式之一，它为实现物理学的大统一提供了新的思路和数学工具。随着研究的深入，这一方程有望在量子引力理论、宇宙学和基础物理学研究中发挥重要作用。