机器学习007:监督学习【回归算法】（线性回归）--股票背后的预测学

你是一家奶茶店的店长。你发现，每当天气越热，店里卖出的冰奶茶就越多。于是你默默记下：昨天30℃，卖了200杯；今天28℃，卖了180杯。那么你猜，如果明天预报是32℃，该准备多少杯奶茶的原料呢？

你大脑里那个模糊的估算过程------"温度更高，就该多备点货"------其实已经触及了人工智能中最基础、最核心的预测思想。而我们将要认识的这位朋友，线性回归算法，就是将这种"凭感觉的估算"变成"靠数据的计算"的数学魔法师。

它可能没有"神经网络"听起来那么酷炫，但它是你通往AI世界的第一块，也是最重要的一块基石。理解它，就像学功夫先扎马步，学音乐先认音符。今天，就让我们像朋友聊天一样，彻底认识它。

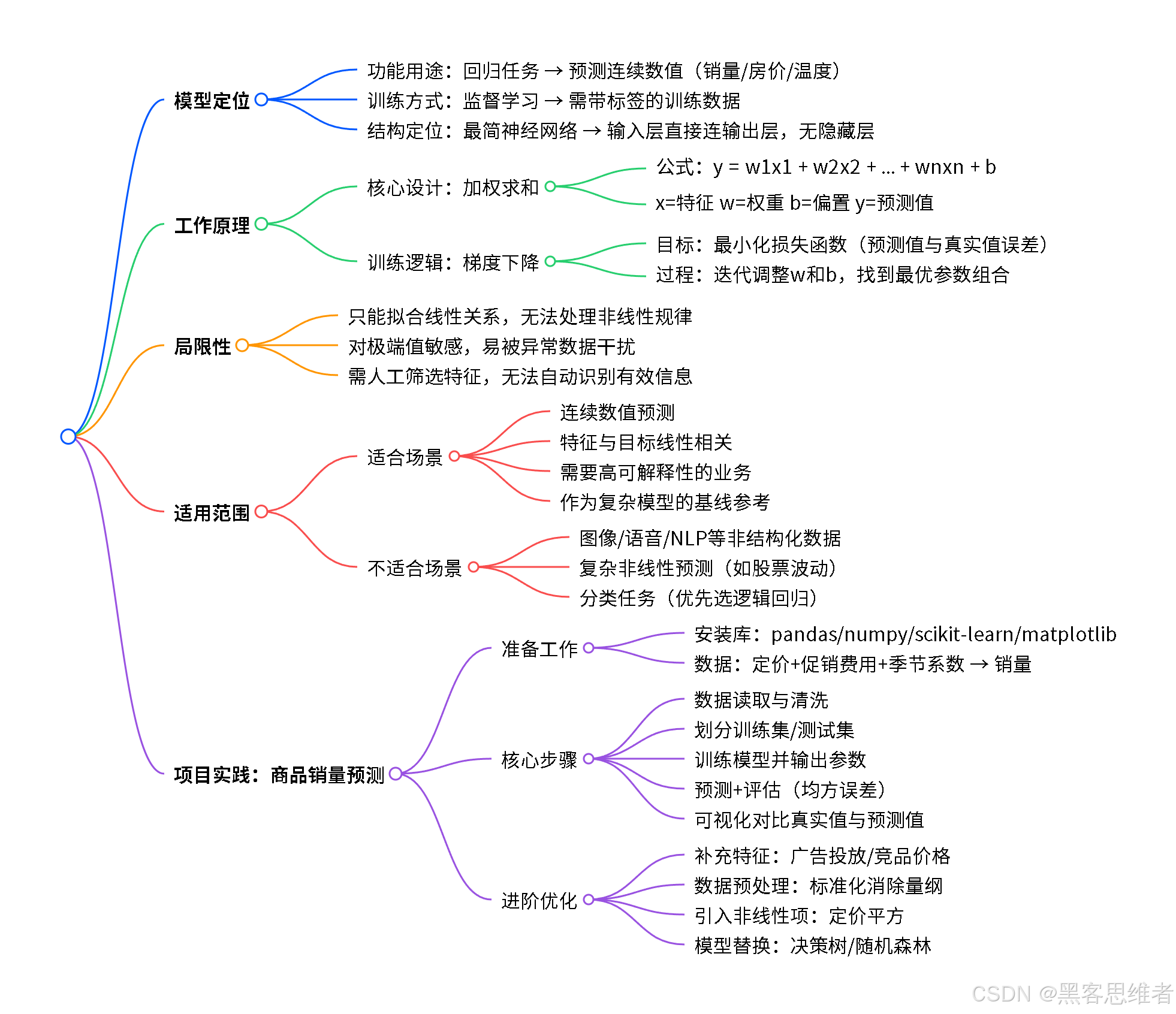
一、身份卡片：它属于哪个"门派"？

在人工智能的"江湖"里，模型种类繁多，我们可以从几个维度给它们贴上标签，方便我们理解线性回归的位置。

• 按功能用途划分 ：它属于 "回归"任务 的鼻祖和代表。"回归"这个词听起来深奥，其实意思很简单：预测一个具体的、连续的数值。比如预测明天的气温（24.5℃）、预测房子的价格（352万元）、预测你的考试成绩（88分）。它不负责做"是或否"的选择（那是"分类"任务的地盘，比如判断图片里是猫还是狗）。
• 按训练方式划分 ：它属于 "监督学习" 家族。这意味着，要训练它，我们必须先准备一份"带答案的习题册"。比如，习题册里每一行都写着"30℃ -> 200杯"、"28℃ -> 180杯"......算法通过反复学习这些已知的"问题"（温度）和"答案"（销量），来找到它们之间的关系，最终学会解答新问题（32℃时是多少杯？）。
• 按结构复杂性划分 ：它是 最基础、最简单的神经网络（特例）。你可以把它想象成一个极度简化的神经网络：只有一个"输入层"（比如温度数据）直接连接到一个"输出层"（预测的销量），中间没有复杂的隐藏层。它的"神经元"计算也极其简单，就是做一次加权求和。

一句话概括它的门派 ：线性回归是监督学习 门派中，专门解决数值预测（回归）问题的基础模型，可以看作是一个结构最简单的神经网络。

---

二、工作原理：像调一杯"完美奶茶"的配方

让我们忘掉数学公式，用你开奶茶店的例子，把线性回归的"大脑"拆开看看。

1. 核心设计：一切皆是"加权求和"

假设你的奶茶销量不只受温度影响，还受"是否周末"（1代表是，0代表不是）和"促销力度"（折扣百分比）的影响。线性回归的核心思想就是：

总销量 = (温度的影响力 × 温度值) + (周末的影响力 × 周末值) + (促销的影响力 × 促销力度) + 一个基础销量

这个"影响力"，在算法里就叫 "权重" 或 "系数" 。而"基础销量"就是 "偏置"，代表当所有因素都为0时（比如温度0℃、非周末、不促销），大概能卖多少杯。

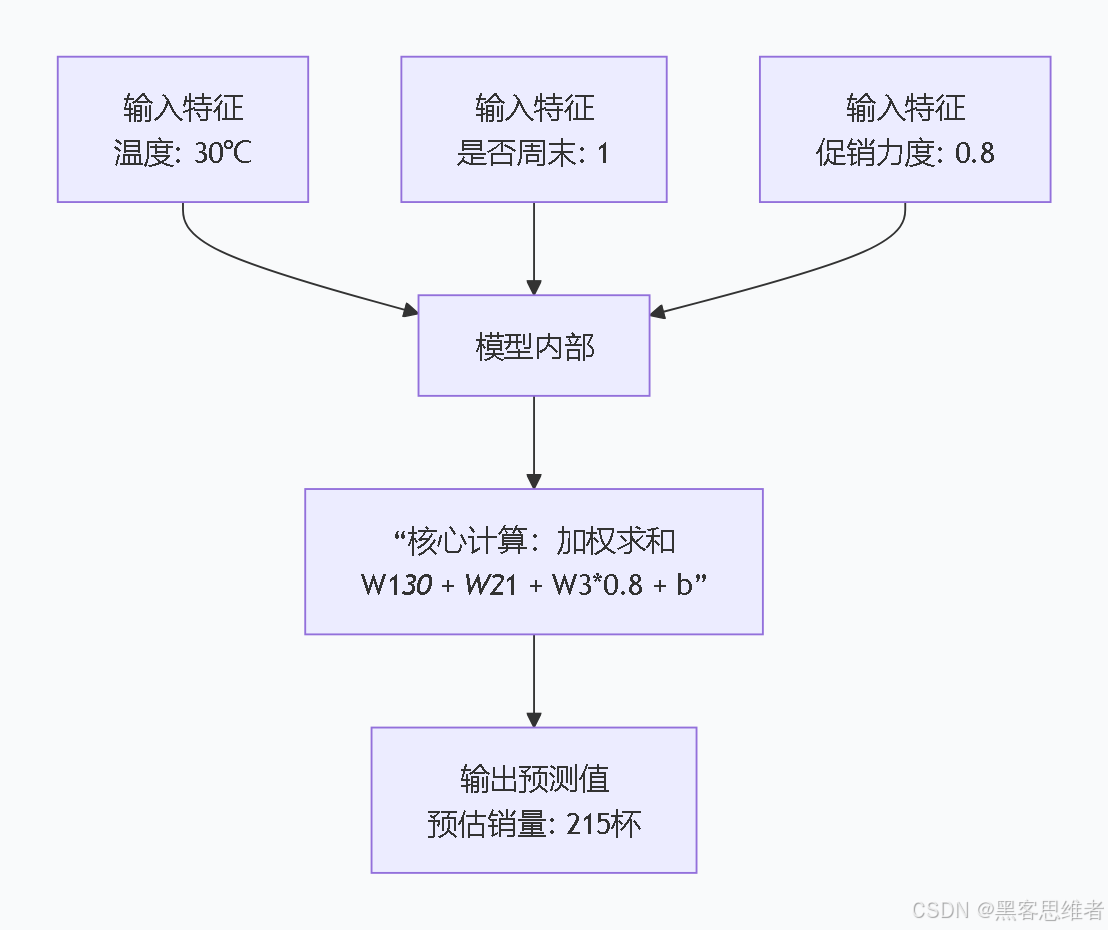
你看，数据就是这样单向、直接地流过去，得到一个预测值。

2. 训练逻辑：如何找到"最佳配方"？（梯度下降）

现在关键来了：我们怎么知道"温度的影响力"具体应该是5还是10？ "基础销量"应该是100还是50？

这个过程就叫 "训练"或"学习"。想象一下：

你面前有一个神奇的奶茶配方机，上面有三个旋钮（分别控制"温度权重"、"周末权重"、"促销权重"）和一个基础量旋钮（"偏置"）。

你手头有过去100天的真实数据（带答案的习题册）。

你的目标是：扭动这些旋钮，使得配方机根据这100天的天气、周末、促销情况计算出来的"预测销量"，和那100天真实的"实际销量"之间的总差距，达到最小。

这个"总差距"，在算法里有一个专业的名字叫 "损失函数" 。我们的目标就是最小化损失函数。

怎么扭旋钮呢？靠猜吗？算法有一个聪明的方法，叫 "梯度下降"。你可以把它理解为：

你被蒙上眼睛，站在一座高低起伏的山丘上（山丘的高度代表"总差距"），你的任务是要走到最低的那个山谷（差距最小的地方）。

虽然看不见，但你可以用脚感受一下哪个方向是"下坡"最陡的。然后，你就朝着那个方向小心翼翼地迈一小步。

到达新位置后，你再感受一下，再找最陡的下坡方向，再迈一步......如此反复，直到你感觉四周都是平路或上坡------恭喜，你很可能已经站在了谷底！

这个"感受下坡方向并迈步"的过程，就是梯度下降。它通过计算数学上的"梯度"（可以理解为指向误差增大最快的方向的反方向），来告诉每个"旋钮"："你应该往哪个方向（增大还是减小）、以多大的力度（学习率）去调整自己"。

公式的通俗亮相：

虽然我们强调理解逻辑，但认识一下它的数学"真容"会让你更踏实。线性回归的核心公式很简单：

`y=w1∗x1+w2∗x2+...+wn∗xn+b y = w1*x1 + w2*x2 + ... + wn*xn + by=w1∗x1+w2∗x2+...+wn∗xn+b

• y: 我们要预测的值（比如销量）。
• x1, x2...xn: 各个输入特征（比如温度、是否周末）。
• w1, w2...wn: 每个特征对应的权重（影响力）。
• b: 偏置（基础量）。

训练的目标，就是找到一组最优的 w1, w2...wn 和 b。

---

三、局限性：它为什么不是"万能药"？

理解了线性回归的强大和精巧，我们更要清醒地认识它的边界。它并非无所不能，它的局限源于其最核心的设计。

1. 局限一：只能刻画"直线"关系

这是它最根本的局限。线性回归，顾名思义，它只能学习和表示特征与结果之间成"直线"比例的关系。

• 生活比喻：它认为"温度每升高1℃，销量永远固定增加10杯"。但现实中更可能是：温度从20℃升到30℃，销量大增；但从35℃升到40℃，因为太热人们可能都不想出门了，销量增长会放缓甚至下降。这种"曲线"关系，线性回归无能为力。
• 专业解释：因为它模型的本质就是一次线性方程，图形是一条直线（或平面/超平面）。对于复杂的非线性关系，它的拟合能力很差。

2. 局限二：对极端值非常敏感

• 生活比喻：假设你100天数据里，有99天销量都在100-200杯之间，但突然有一天因为附近开演唱会，销量暴增到1000杯。这个"极端值"会像一块巨大的磁铁，把线性回归找到的那条"最佳直线"狠狠地拽向它，导致这条直线对大多数正常日子的预测变得非常不准。
• 专业解释：线性回归的损失函数（通常是均方误差）会放大较大误差的影响。一个极端值造成的巨大误差，会在训练中被重点"照顾"，从而过度影响模型参数。

3. 局限三：需要人为筛选特征

它不会自动理解特征的意义。如果你把"店铺编号"、"随机数"这些毫无关系的特征也喂给它，它也会老老实实地去计算一个"权重"，这会导致模型学到无意义的噪音，从而降低预测效果。特征工程（挑选、处理有效特征）在使用线性回归时至关重要。

---

四、使用范围：什么样的问题该请它出马？

了解了能做什么和不能做什么，它的"工作职责"就清晰了。

✅ 适合用它解决的问题（它的主场）：

1. 预测连续的数值：这是它的老本行。
2. 特征与目标之间存在清晰、近似的线性趋势：当你把数据画成散点图，能看出大致的"直线"走向。
3. 需要模型高度可解释性：线性回归的"权重"直接告诉你每个特征有多大的正面或负面影响。比如在房价预测中，你可以明确说"面积每增加1平米，房价平均上涨5000元"，这在商业决策中极具价值。
4. 作为复杂模型的基线：在任何预测任务开始前，先用线性回归跑一个结果，这个结果将成为衡量更复杂模型（如神经网络）是否真正有效的"基准线"。

❌ 不适合用它解决的问题（请另请高明）：

1. 图像识别、语音识别：这些数据高度复杂、非结构化，特征间是极深的非线性关系。
2. 自然语言处理（如机器翻译、情感分析）：语言数据是离散的、序列化的，需要能理解上下文和语序的模型（如RNN, Transformer）。
3. 复杂非线性预测：比如股票价格波动、生物信号分析等，数据背后的规律不是直线能描绘的。
4. 分类问题：虽然可以通过设置阈值变通使用，但有更适合的"分类器"（如逻辑回归、决策树）。

---

五、应用场景：它就在我们身边

别看它简单，线性回归在工业和生活中无处不在，是许多智能决策的"幕后军师"。

1. 电商销量预测与库存管理

• 作用：电商平台（如淘宝、京东）根据过往数据（历史销量、节假日、促销活动、广告投入、竞品价格等），利用线性回归预测未来一段时间内某商品的销量。
• 价值：指导仓储提前备货，优化物流资源分配，避免缺货或库存积压。这是供应链智能化的基础。

2. 房地产估价（房价预测）

• 作用 ：购房平台（如贝壳、安居客）的"房价评估"功能，其核心模型之一就是线性回归。它会考虑房屋的面积、房间数、楼层、房龄、地理位置（可量化为到市中心距离或学区评分） 等多个特征，给出一个估算价格。
• 价值：为买家、卖家和银行提供快速、量化的价格参考，是房地产市场交易的重要工具。

3. 教育领域的成绩影响因素分析

• 作用 ：教育研究者想了解什么因素最影响学生的期末考试成绩。他们收集数据：每周学习小时数、家庭收入、出勤率、父母教育水平等，用线性回归进行分析。
• 价值：模型输出的"权重"会直接显示，例如"每周学习时间每增加1小时，平均成绩提高1.2分"。这能帮助学校和家长识别关键影响因素，进行针对性干预。

4. 互联网广告的点击率预估

• 作用 ：在早期或某些简化场景中，线性回归被用于预测一个广告被用户点击的概率。特征可能包括用户年龄、性别、历史点击行为、广告位尺寸、广告文本长度等。
• 价值：平台可以根据预估的点击率对广告进行排序和定价，实现流量价值最大化。虽然现在更多被更复杂的模型替代，但其思想仍是基石。

5. 宏观经济指标分析

• 作用 ：经济学家研究国民收入与消费支出 之间的关系（凯恩斯消费函数）、教育投入与GDP增长之间的关系等，常常首选线性回归来量化这种影响。
• 价值：为政府制定财政政策、教育政策等提供简洁有力的数据支持。

---

总结：你的第一块AI基石

好了，我们的线性回归之旅就要结束了。现在，请你再回想一下那家奶茶店。从"感觉天热该多备货"，到用算法精确计算出"32℃时应备货220杯"，这其中蕴含的，正是数据科学和人工智能最朴素的起点：从经验中学习规律，用规律预测未来。

一句话概括线性回归的核心价值： 它是一种寻找数据间简单、直观的线性规律 ，并用于做出靠谱数值预测 的、高度可解释的基础工具。

作为初学者，学习线性回归的重点不在于记忆公式，而在于透彻理解其 "加权求和"的核心思想 和 "通过减少误差来学习"的训练逻辑 ，同时清醒地认识其 "只能拟合直线"的根本局限。

它就像一把直尺，能量出直线的距离，却画不出优美的曲线。但正因为先有了这把可靠的直尺，你才能更好地理解后来那些能画出曲线、甚至三维立体画的复杂工具（如多项式回归、决策树、神经网络）究竟高明在何处。

线性回归预测商品销量：零基础项目实践

本次实践将用 Python 实现「基于线性回归的商品销量预测」，核心思路是：先分析影响销量的关键因素（比如促销力度、定价、季节等），再用历史数据训练线性回归模型，最终预测未来销量。全程代码简单易懂，零基础也能跟着做。

一、项目准备

1. 环境安装

需要安装 3 个核心库：

• pandas：处理数据（读取、清洗）
• numpy：数值计算
• scikit-learn：实现线性回归模型
• matplotlib：可视化结果（可选，方便理解）

打开命令行，输入安装命令：

pip install pandas numpy scikit-learn matplotlib

2. 数据准备

我们模拟一份「某零食商品的月度销售数据」，包含 3 个特征（自变量）和 1 个目标值（因变量）：

月份	定价（元）	促销费用（千元）	季节系数（1=旺季/0=淡季）	销量（千件）
1	15	8	0	20
2	14	10	0	25
3	13	12	1	35
4	12	15	1	40
5	14	9	1	30
6	15	7	0	18
7	12	14	0	32
8	11	16	1	45
9	13	11	1	38
10	14	8	0	22
11	12	13	1	39
12	15	9	0	21

将上述数据保存为 sales_data.csv 文件（可直接复制到 Excel 后另存为 CSV）。

二、核心代码实现

步骤 1：导入库并读取数据

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# 读取数据
data = pd.read_csv("sales_data.csv")
# 查看数据基本信息（可选，确认无缺失值）
print("数据预览：")
print(data.head())
print("\n数据是否有缺失值：")
print(data.isnull().sum())

步骤 2：划分特征和目标值

# 特征（影响销量的因素）：定价、促销费用、季节系数
X = data[["定价（元）", "促销费用（千元）", "季节系数（1=旺季/0=淡季）"]]
# 目标值：销量
y = data["销量（千件）"]

# 划分训练集（80%）和测试集（20%）：用训练集训练模型，测试集验证效果
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

步骤 3：训练线性回归模型

# 初始化线性回归模型
model = LinearRegression()
# 用训练数据训练模型
model.fit(X_train, y_train)

# 输出模型参数（理解：每个特征对销量的影响程度）
print("\n模型系数（特征对销量的影响）：")
print(f"定价每涨1元，销量变化：{model.coef_[0]:.2f} 千件")
print(f"促销费用每增1千元，销量变化：{model.coef_[1]:.2f} 千件")
print(f"旺季（对比淡季）销量变化：{model.coef_[2]:.2f} 千件")
print(f"模型截距：{model.intercept_:.2f}")

步骤 4：模型预测与评估

# 用测试集预测销量
y_pred = model.predict(X_test)

# 评估模型（均方误差：数值越小，模型预测越准）
mse = mean_squared_error(y_test, y_pred)
print(f"\n模型均方误差（越小越好）：{mse:.2f}")

# 对比真实销量和预测销量
print("\n真实销量 vs 预测销量：")
compare = pd.DataFrame({"真实销量": y_test, "预测销量": np.round(y_pred, 1)})
print(compare)

步骤 5：预测未来销量（示例）

假设下个月是「旺季」，定价 13 元，促销费用 12 千元，预测销量：

# 构造未来数据（格式要和训练数据一致）
future_data = np.array([[13, 12, 1]])
# 预测销量
future_sales = model.predict(future_data)
print(f"\n未来月度预测销量：{future_sales[0]:.1f} 千件")

步骤 6：可视化结果（可选）

# 对比真实销量和预测销量的折线图
plt.rcParams["font.sans-serif"] = ["SimHei"]  # 解决中文显示
plt.figure(figsize=(10, 6))
plt.plot(range(len(y_test)), y_test, label="真实销量", marker="o")
plt.plot(range(len(y_test)), y_pred, label="预测销量", marker="x")
plt.xlabel("测试集样本序号")
plt.ylabel("销量（千件）")
plt.title("线性回归模型：真实销量 vs 预测销量")
plt.legend()
plt.grid(True)
plt.show()

三、结果解读（示例）

运行代码后，你会看到类似这样的结论：

1. 定价每涨1元，销量约减少 2.5 千件（符合常识：越贵买的人越少）；
2. 促销费用每增1千元，销量约增加 1.8 千件（促销能提升销量）；
3. 旺季比淡季销量多约 5 千件（季节影响明显）；
4. 测试集的预测销量和真实销量差距很小（均方误差低），说明模型拟合效果不错；
5. 示例中未来月度预测销量约 38.5 千件。

四、进阶优化（可选）

如果想让模型更准，可以试试这些小技巧：

1. 补充更多数据：比如加入「广告投放量」「竞品价格」等特征；
2. 数据预处理：对定价、促销费用做「标准化」（消除量纲影响）；
3. 尝试非线性特征：比如加入「定价的平方」（模拟"定价过高后销量骤降"的规律）；
4. 换模型：如果线性回归效果一般，可尝试决策树、随机森林等非线性模型。

五、核心知识点科普

线性回归的本质是「找一条最优直线（或平面），拟合特征和销量的关系」：

• 对于单个特征（比如仅用促销费用预测销量），就是找 销量 = a×促销费用 + b 中的最优 a 和 b；
• 多个特征时，就是 销量 = a×定价 + b×促销费用 + c×季节系数 + d，模型会自动算出最优的 a、b、c、d；
• 它的优势是简单易懂、结果可解释（能清楚看到每个因素对销量的影响），适合入门级销量预测。

这个项目全程用基础代码实现，没有复杂公式，你可以直接复制代码，替换成自己的商品销量数据（比如门店的饮料销量、网店的服饰销量），就能快速做一份销量预测啦！