算法基础-图论基础

1. 图的基本概念

1.1 图的定义

图 G 是由顶点集 V 和边集 E 组成，记为 G=(V,E)，其中 V(G) 表示图 G 中顶点的有限非空集；E(G) 表示图 G 中顶点之间的关系（边）集合。若 V={v1​,v2​,...,vn​}，则用 ∣V∣ 表示图 G 中顶点的个数，也称图 G 的阶，E={(u,v)∣u∈V,v∈V}，用 ∣E∣ 表示图 G 中边的条数。

图是较线性表和树更为复杂的数据结构。

• 线性表中，除第一个和最后一个元素外，每个元素只有一个唯一的前驱和唯一的后继结点，元素和元素之间是一对一的关系；
• 在树形结构中，数据元素之间有着明显的层次关系，每个元素有唯一的双亲，但可能有多个孩子，元素和元素之间是一对多的关系；
• 而图形结构中，元素和元素之间的关系更加复杂，结点和结点之间的关系是任意的，任意两个结点之间都可能相关，图中元素和元素之间是多对多的关系。

---

1.2 有向图和⽆向图

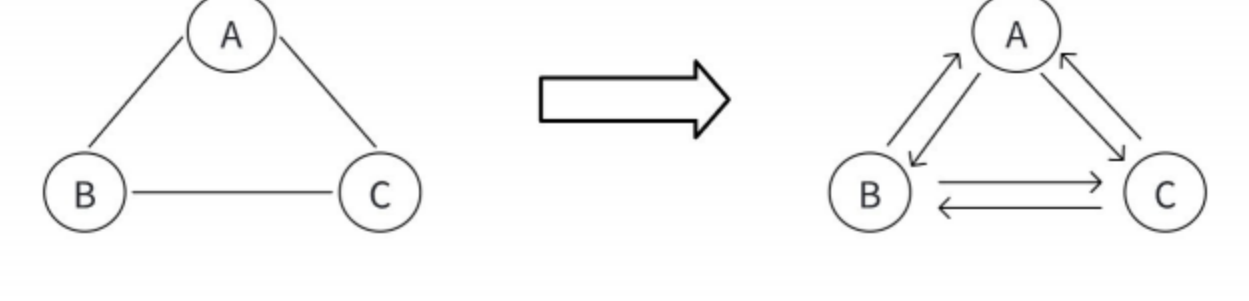
图根据边的类型，可以分为 ⽆向图和有向图 ：

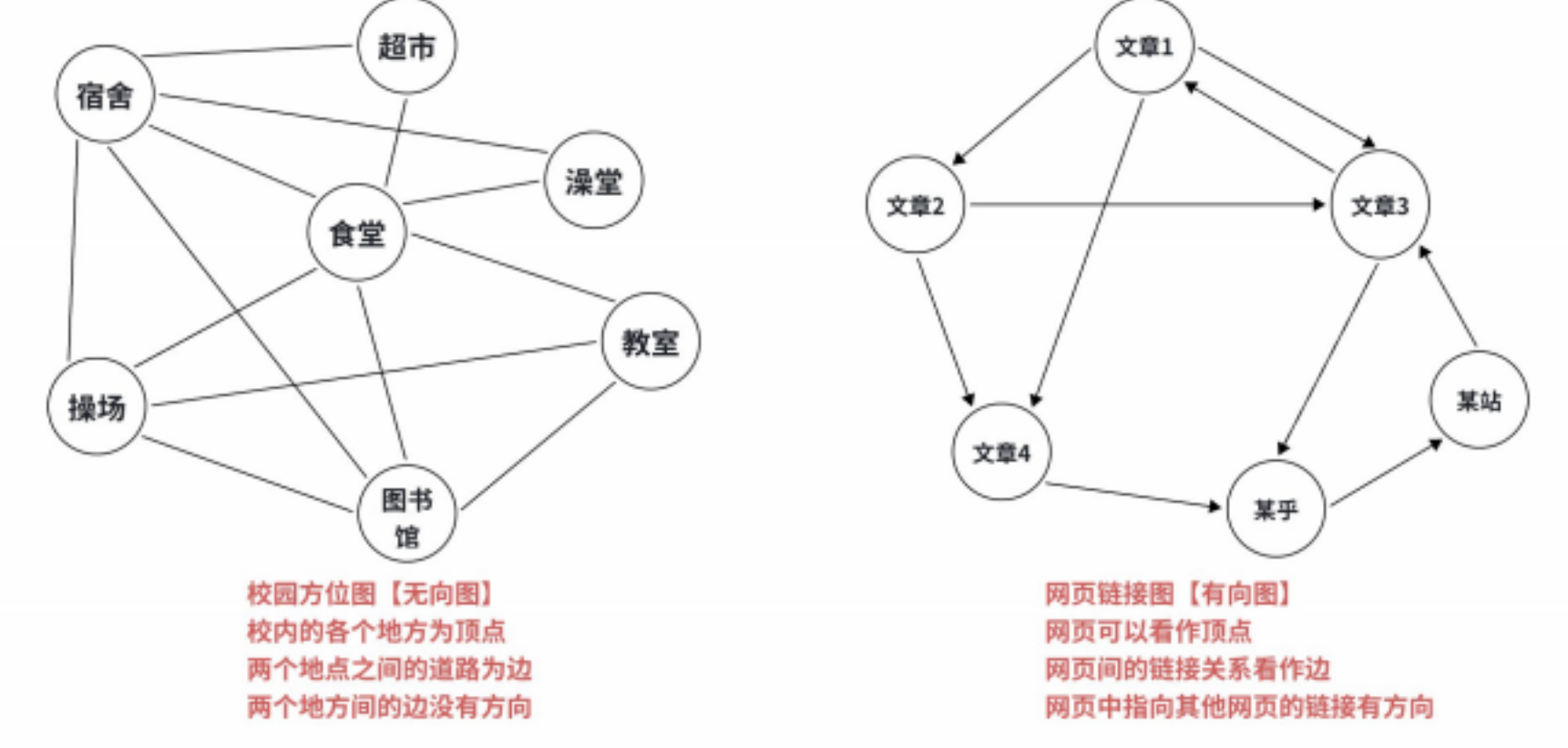
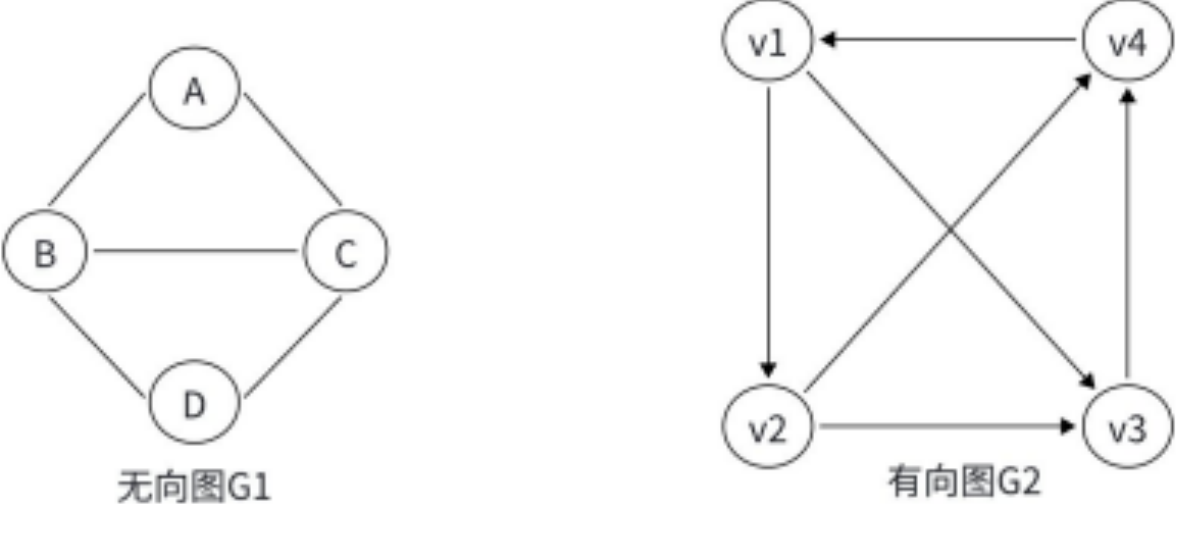
在图相关的算法中，我们可以将⽆向图中的边看成两条⽅向相反的有向边，从⽽将⽆向图转化为有向 图：

1.3 简单图与多重图

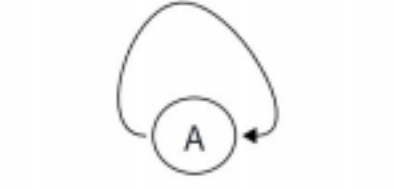
⾃环：⾃⼰指向⾃⼰的⼀条边。

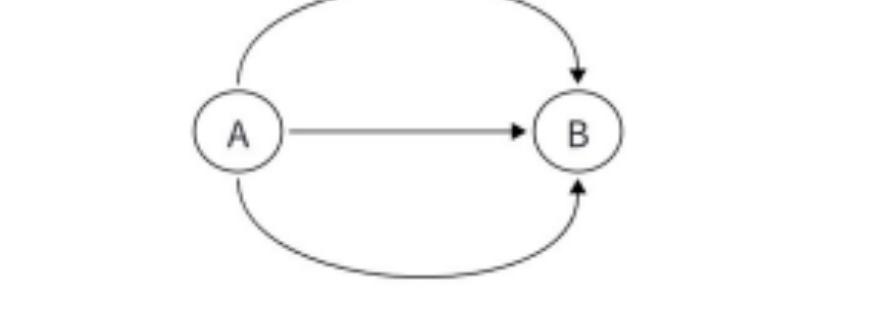
重边：图中存在两个或两个以上完全相同的边。

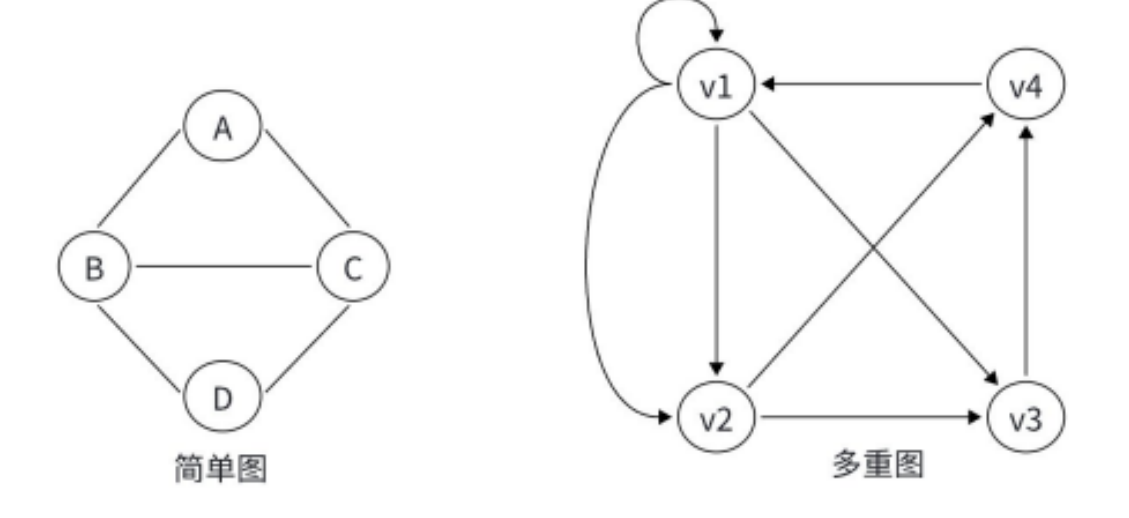
简单图：若图中没有重边和⾃环，为简单图。
多重图：若图中存在重边或⾃环，为多重图。

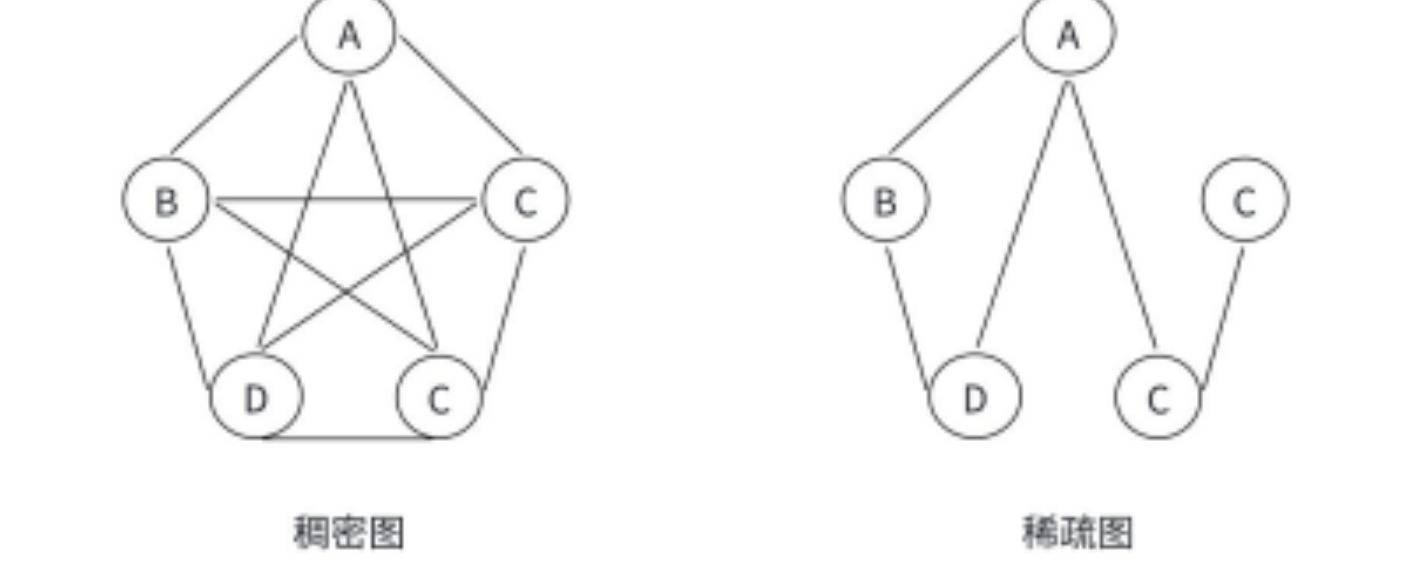
1.4 稠密图和稀疏图

有很少条边(如 e < nlog 2 n )的图称为稀疏图，反之称为稠密图。

1.5 顶点的度

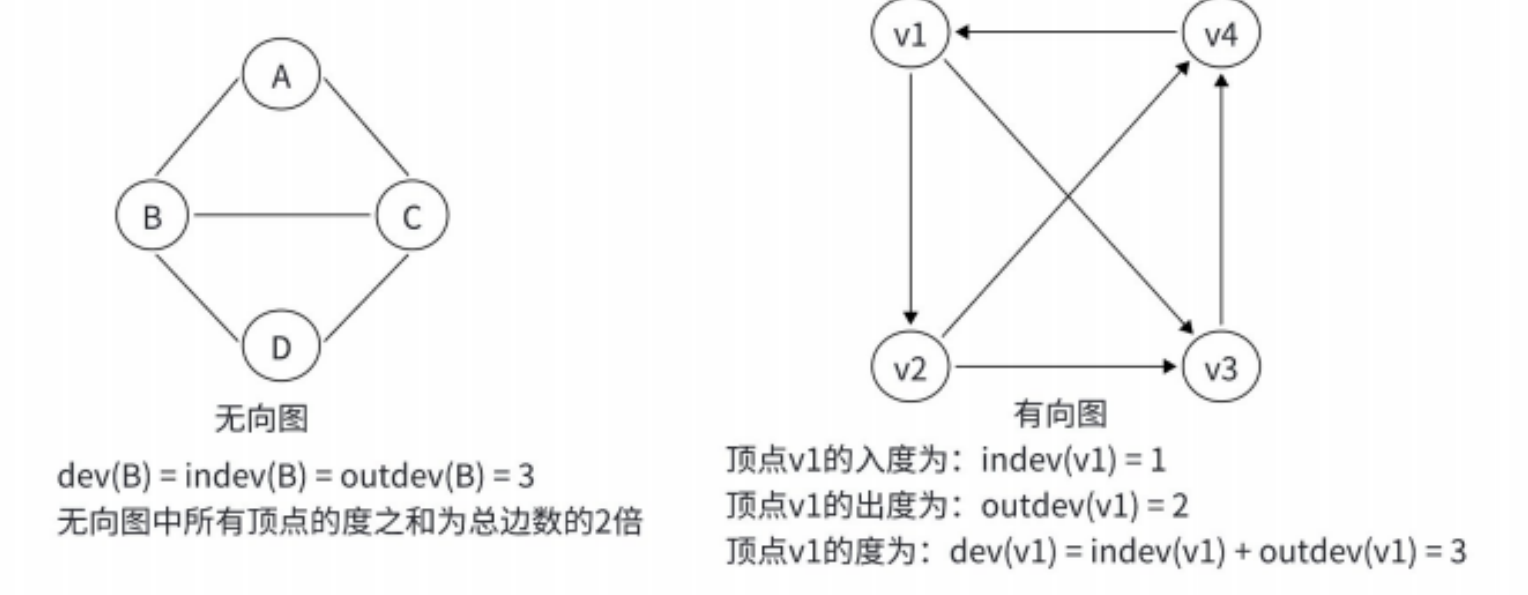
顶点 v 的度是指与它相关联的边的条数，记作 deg(v)。由该顶点发出的边称为顶点的出度，到达该顶
点的边称为顶点的⼊度。
• ⽆向图中，顶点的度等于该顶点的⼊度(indev)和出度(outdev)，即 deg(v) = indeg(v) =
outdeg(v)。
• 有向图中，顶点的度等于该顶点的⼊度与出度之和，其中顶点 v 的⼊度 indeg(v) 是以 v 为终点的有
向边的条数，顶点 v 的出度 outdeg(v) 是以 v 为起始点的有向边的条数，deg(v) = indeg(v) +
outdeg(v)

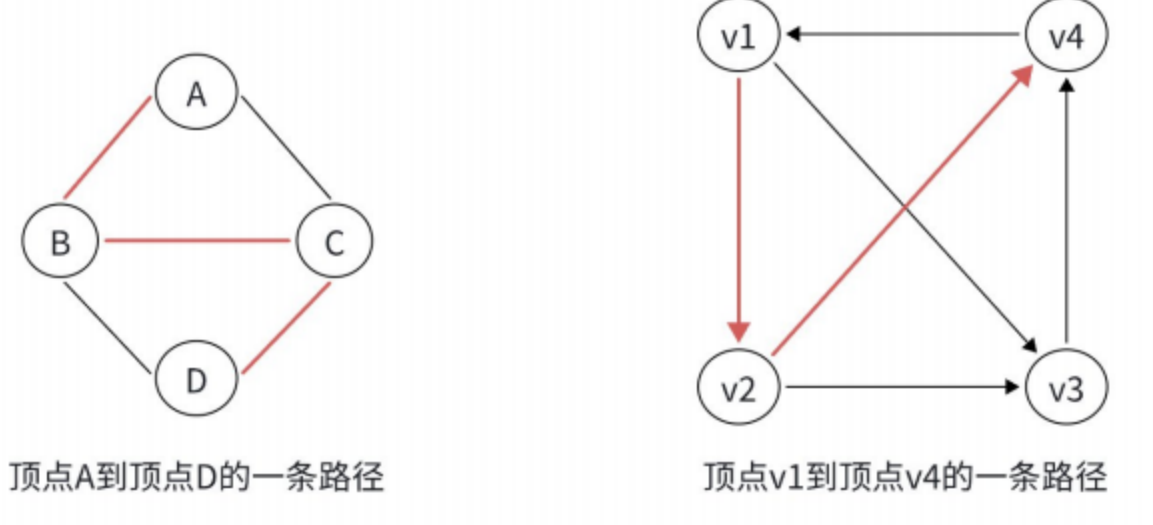
1.6 路径

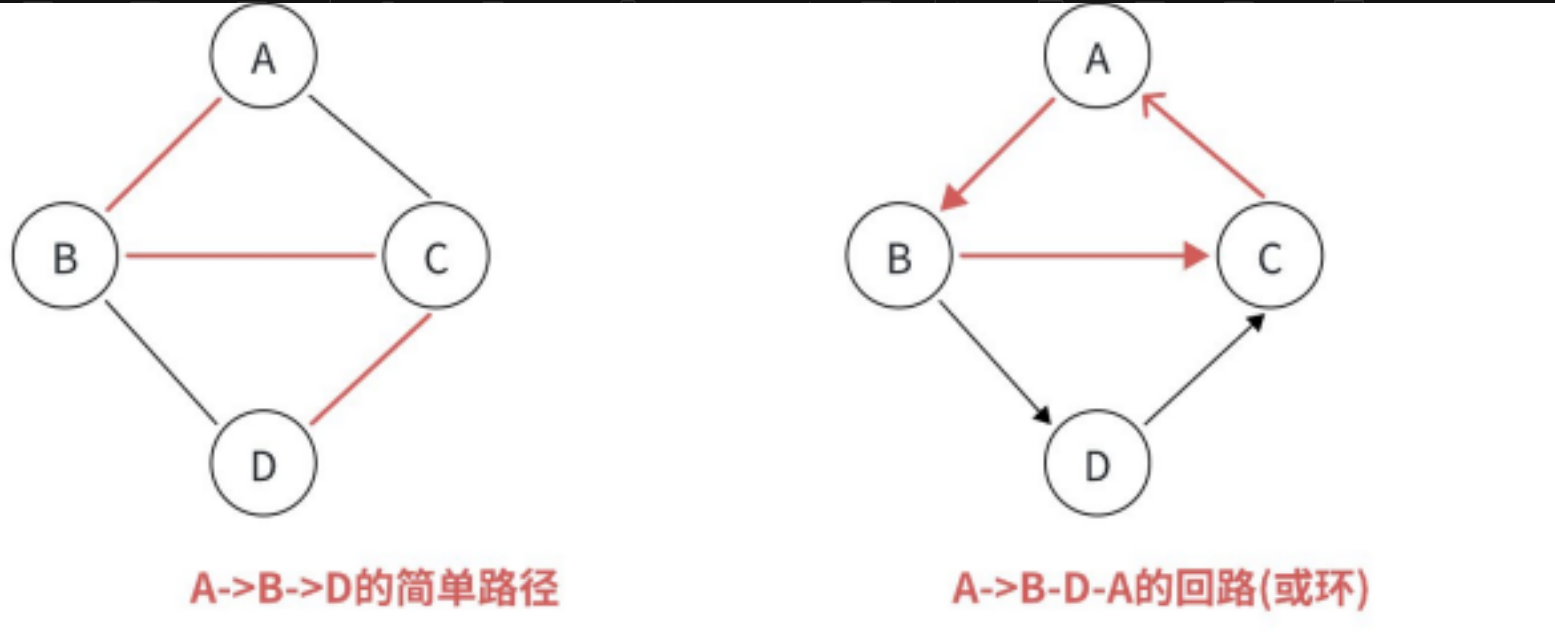
1.7 简单路径与回路

若路径上各顶点v 1 , v 2 , v 3 , ..., v m 均不重复，则称这样的路径为简单路径。若路径上第⼀个顶点
V1和最后⼀个顶点Vm 相同，则称这样的路径为回路或环。

1.8 路径⻓度和带权路径⻓度

某些图的边具有与它相关的数值，称其为该边的权值。这些权值可以表⽰两个顶点间的距离、花费的 代价、所需的时间等。⼀般将该种带权图称为 ⽹络 。

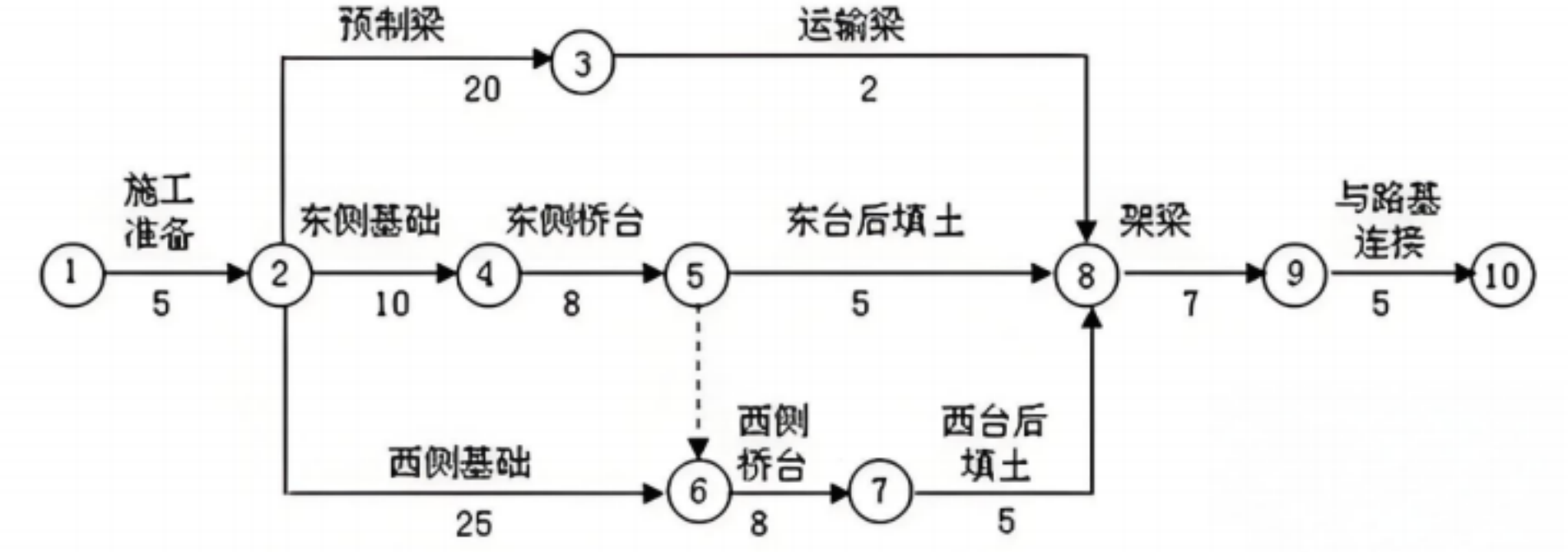
某⼯程施⼯周期图
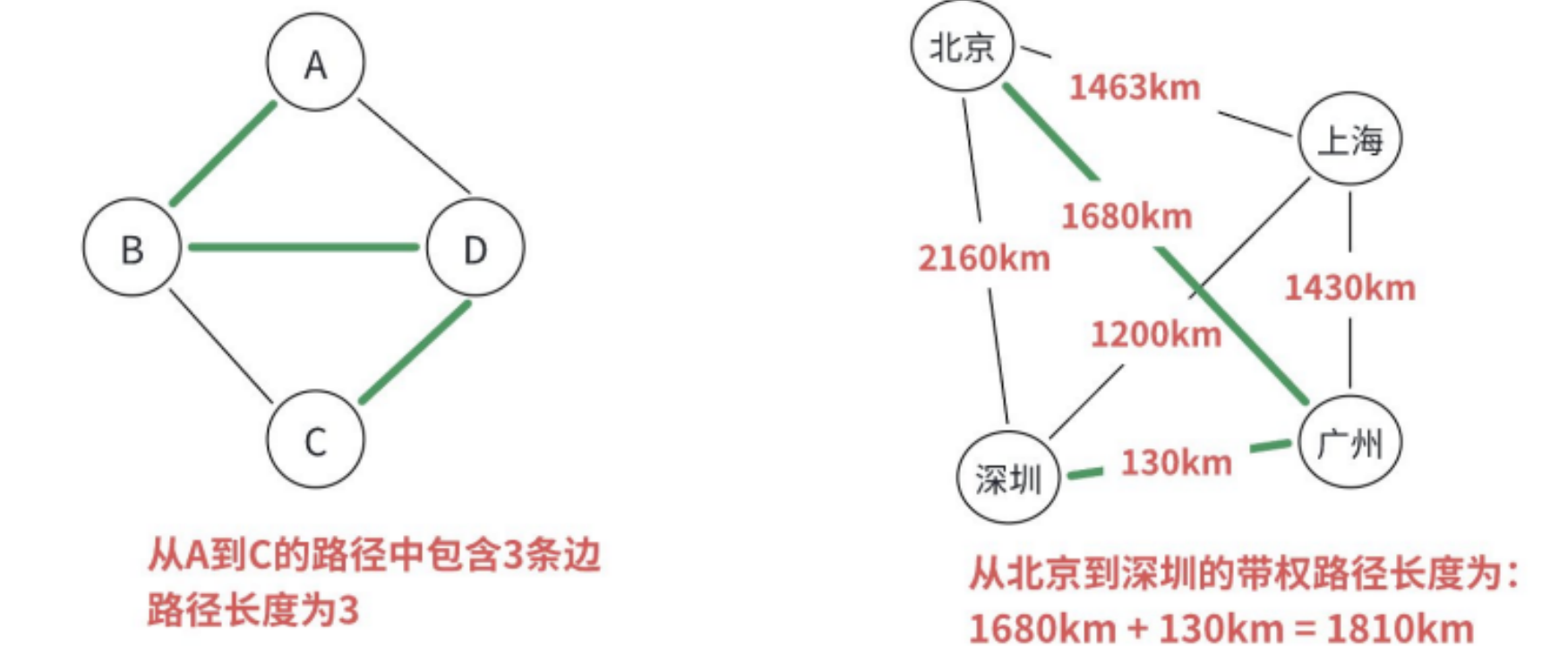
对于不带权的图，⼀条路径的路径⻓度是指该路径上的边的条数。
对于带权的图，⼀条路径的路径⻓度是指该路径上各个边权值的总和。

1.9 ⼦图

设图 G = { V , E } 和图 G ′ = { V ′ , E ′ } ，若 V ′ ∈ V 且 E ′ 属于 E ，则称 G ′ 是 G 的⼦图。若
有 V ( G ′ ) = V ( G ) 的⼦图 G ′ ，则称 G ′ 为 G 的⽣成⼦图。
相当于就是在原来图的基础上，拿出来⼀些顶点和边，组成⼀个新的图。但是要注意，拿出来的点和
边要能构成⼀个图才⾏。

---

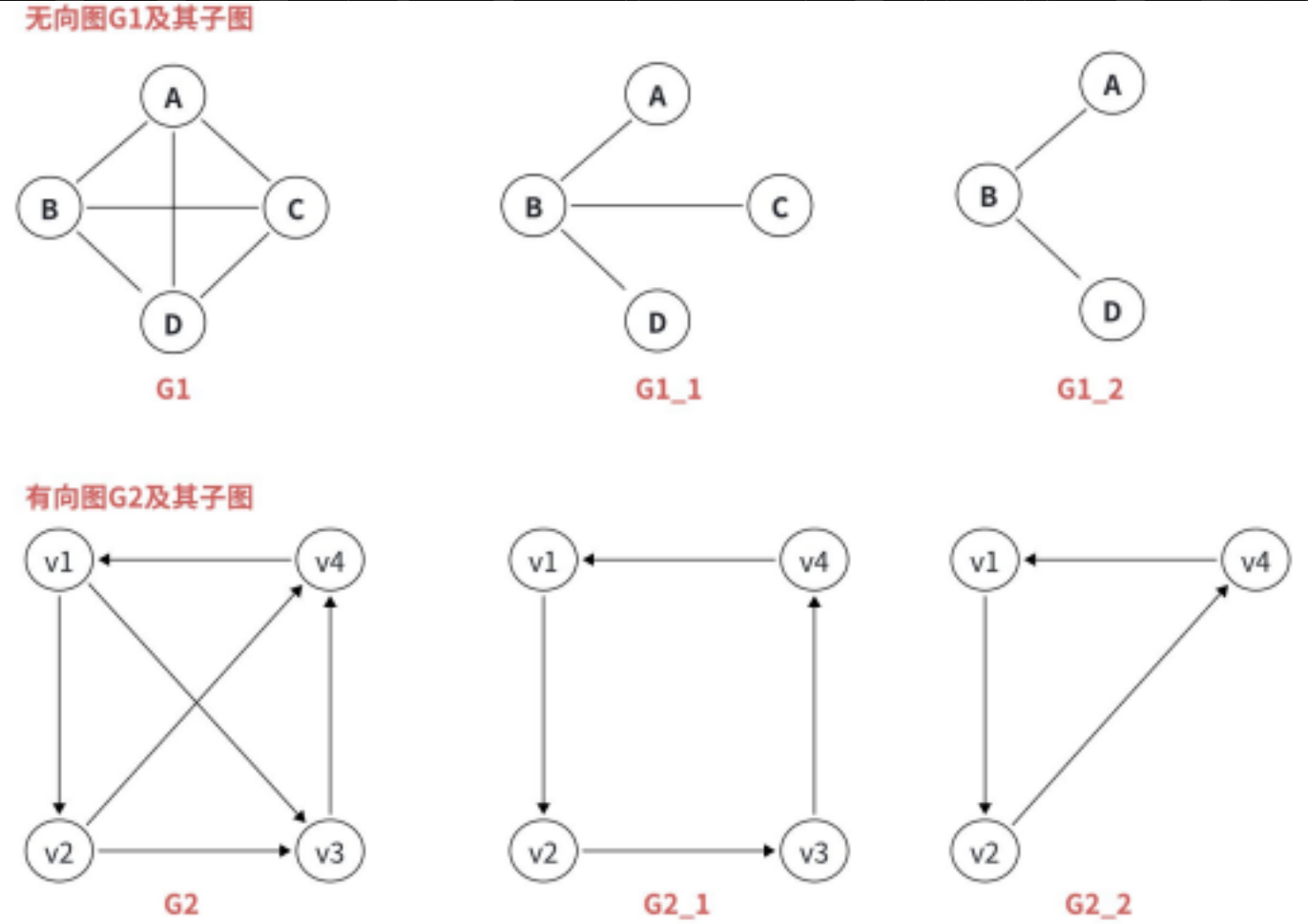
G1_1 和 G1_2 为⽆向图 G1 的⼦图，G1_1 为 G1 的⽣成⼦图。
G2_1 和 G2_2 为有向图 G2 的⼦图，G2_1 为 G2 的⽣成⼦图。

---

1.10 连通图与连通分量

在⽆向图中，若从顶点 v 1 到顶点 v 2 有路径，则称顶点 v 1 与顶点 v 2 是连通的。如果图 G 中任意
⼀对顶点都是连通的，则图 G 称为连通图，否则称为⾮连通图。
• 假设⼀个图有 n 个顶点，如果边数⼩于 n - 1，那么此图⼀定是⾮连通图。
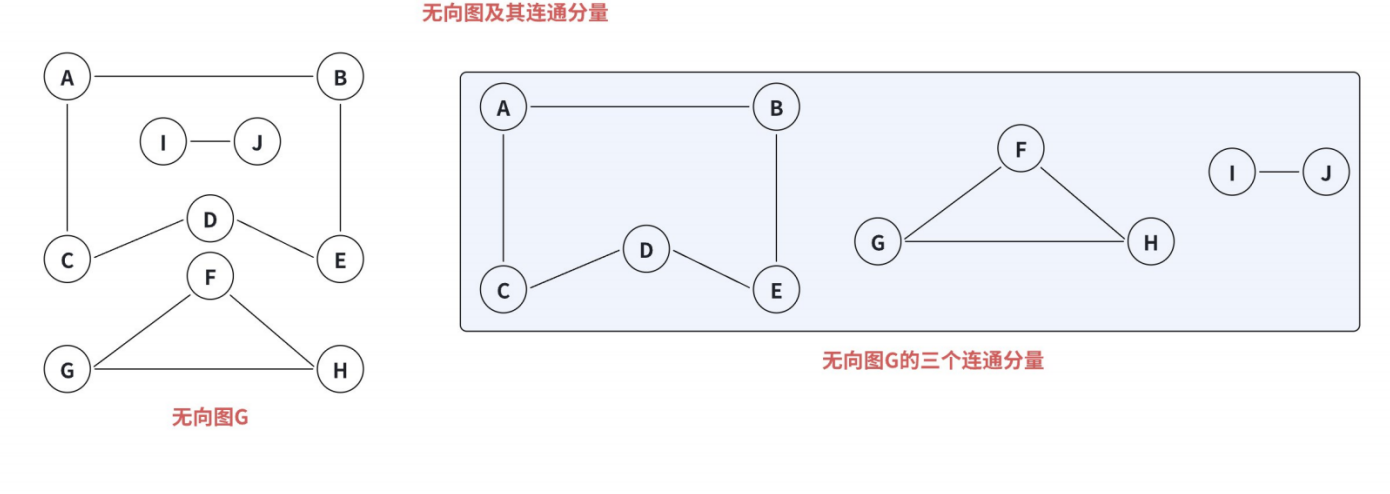
• 极⼤联通⼦图：⽆向图中，拿出⼀个⼦图，这个⼦图包含尽可能多的点和边。
• 连通分量：⽆向图中的极⼤连通⼦图称为连通分量。

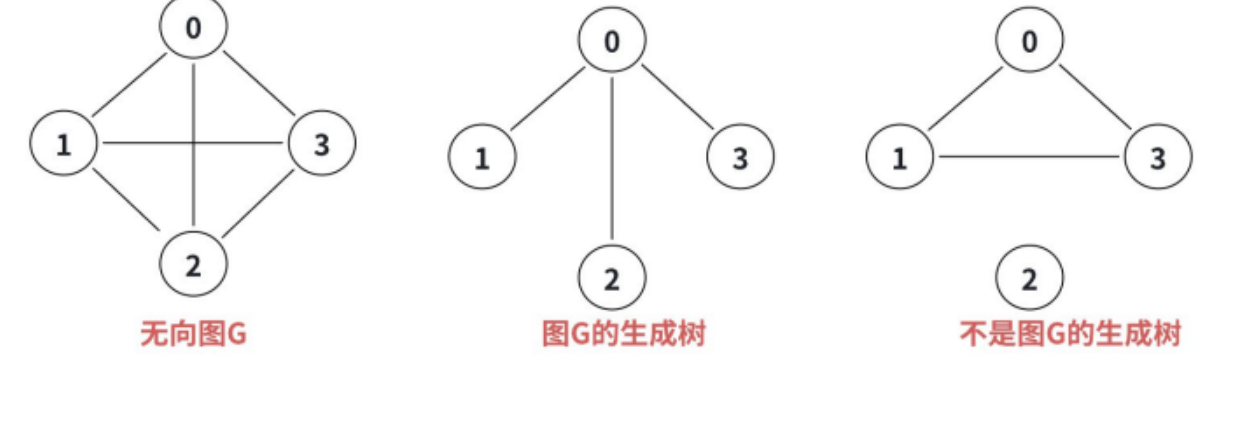
1.11 ⽣成树

连通图的⽣成树是包含图中全部顶点的⼀个极⼩连通⼦图。若图中顶点数为 n，则它的⽣成树含有 n - 1 条边。对⽣成树⽽⾔，若砍去⼀条边，则会变成⾮连通图，若加上⼀条边则会形成⼀个回路。

2. 图的存储和遍历

图的存储有两种： 邻接矩阵和邻接表：
• 其中，邻接表的存储⽅式与树的孩⼦表⽰法完全⼀样。因此，⽤ vector 数组以及链式前向星就能实 现。
• ⽽邻接矩阵就是⽤⼀个⼆维数组，其中 edges[i][j] 存储顶点 i 与顶点 j 之间，边的信
息。
图的遍历分两种：DFS 和 BFS，和树的遍历⽅式以及实现⽅式完全⼀样。因此，可以仿照树这个数据
结构来学习。

---

2.1 邻接矩阵

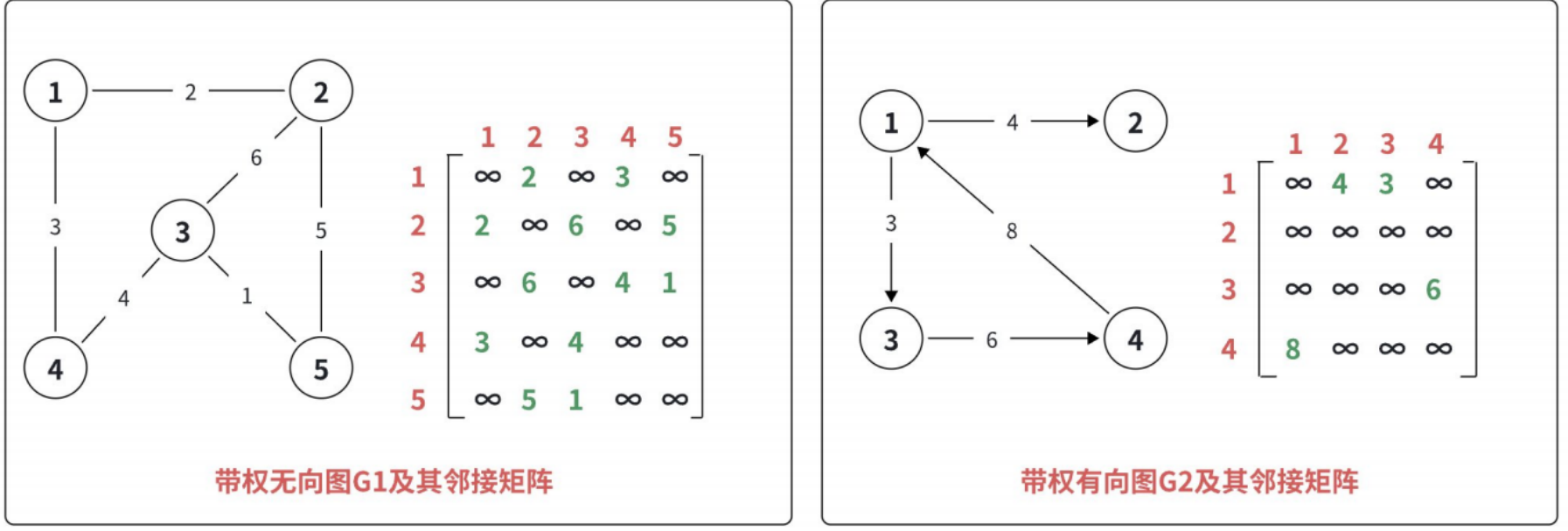
邻接矩阵，指⽤⼀个矩阵(即⼆维数组)存储图中边的信息(即各个顶点之间的邻接关系)，存储顶点之间 邻接关系的矩阵称为邻接矩阵。
对于带权图⽽⾔，若顶点 v i 和 v j 之间有边相连，则邻接矩阵中对应项存放着该边对应的权值，若顶 点 v i 和 v j 不相连，则⽤ ∞ 来代表这两个顶点之间不存在边。
对于不带权的图，可以创建⼀个⼆维的 bool 类型的数组，来标记顶点 v i 和 v j 之间有边相连。

【注意】
矩阵中元素个数为nxn ，即空间复杂度为 O(n^2)， 为顶点个数，和实际边的条数⽆关， 适合存
储稠密图。

代码实现：

#include <iostream>
#include <cstring>
using namespace std;
const int N = 1010;
int n, m;
int edges[N][N];
int main()
{
memset(edges, -1, sizeof edges);
cin >> n >> m; // 读⼊结点个数以及边的个数
for(int i = 1; i <= m; i++)
{
int a, b, c; cin >> a >> b >> c;
// a - b 有⼀条边，权值为 c
edges[a][b] = c;
// 如果是⽆向边，需要反过来再存⼀下
edges[b][a] = c;
}
return 0;
}

2.2 vector 数组

和树的存储⼀模⼀样，只不过如果存在边权的话，我们的 vector 数组⾥⾯放**⼀个结构体或者是 pair**即可。

代码实现：

#include <iostream>
#include <vector>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e5 + 10;
int n, m;
vector<PII> edges[N];
int main()
{
cin >> n >> m; // 读⼊结点个数以及边的个数
for(int i = 1; i <= m; i++)
{
int a, b, c; cin >> a >> b >> c;
// a 和 b 之间有⼀条边，权值为 c
edges[a].push_back({b, c});
// 如果是⽆向边，需要反过来再存⼀下
edges[b].push_back({a, c});
}
return 0;
}

2.3 链式前向星

和树的存储⼀模⼀样，只不过如果存在边权的话，我们多创建⼀维数组，⽤来存储边的权值即可。

代码实现：

#include <iostream>
using namespace std;

// 常量定义：N是顶点的最大数量（1e5+10，能存10万个顶点）
const int N = 1e5 + 10;

// 链式前向星核心数组（关键！）
int h[N];        // 头数组：h[a] = 以a为起点的第一条边的编号
int e[N * 2];    // 边数组：e[id] = 编号为id的边的终点（乘2是因为无向图，每条边要存2次）
int ne[N * 2];   // 下一条边数组：ne[id] = 编号为id的边的下一条边编号
int w[N * 2];    // 权值数组：w[id] = 编号为id的边的权值
int id;          // 边的计数器：每添加一条边，id+1（初始默认是0）

int n, m;        // n=顶点总数，m=边的总数

// 新增边的函数：添加一条"从a到b、权值为c"的有向边
void add(int a, int b, int c)
{
    id++;                // 1. 给这条边分配唯一编号（id从1开始）
    e[id] = b;           // 2. 记录这条边的终点是b
    w[id] = c;           // 3. 记录这条边的权值是c
    ne[id] = h[a];       // 4. 把新边的"下一条边"指向a原来的第一条边
    h[a] = id;           // 5. 把a的第一条边更新为当前新边（头插法核心）
}

int main()
{
    cin >> n >> m; // 1. 读入：顶点个数n，边的个数m
    for(int i = 1; i <= m; i++) // 2. 遍历m条边，逐个添加
    {
        int a, b, c; 
        cin >> a >> b >> c; // 读入一条边：起点a，终点b，权值c
        // 3. 无向图：a→b和b→a各存一次（因为无向边双向通行）
        add(a, b, c); 
        add(b, a, c);
    }
    return 0;
}

---

2.4 DFS

和树的遍历⽅式⼀模⼀样，⼀条路⾛到⿊~

1. ⽤邻接矩阵的⽅式存储

代码实现：

#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 1010;
int n, m;
int edges[N][N];
bool st[N]; // 标记哪些点已经访问过
void dfs(int u)
{
cout << u << endl;
st[u] = true;
// 遍历所有孩⼦
for(int v = 1; v <= n; v++)
{
// 如果存在 u->v 的边，并且没有遍历过
if(edges[u][v] != -1 && !st[v])
{
dfs(v);
}
}
}
int main()
{
memset(edges, -1, sizeof edges);
cin >> n >> m; // 读⼊结点个数以及边的个数
for(int i = 1; i <= m; i++)
{
int a, b, c; cin >> a >> b >> c;
// a - b 有⼀条边，权值为 c
edges[a][b] = c;
// 如果是⽆向边，需要反过来再存⼀下
edges[b][a] = c;
}
return 0;
}

---

2. ⽤ vector 数组的⽅式存储

代码实现：

#include <iostream>
#include <vector>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e5 + 10;
int n, m;
vector<PII> edges[N];
bool st[N]; // 标记哪些点已经访问过
void dfs(int u)
{
cout << u << endl;
st[u] = true;
// 遍历所有孩⼦
for(auto& t : edges[u])
{
// u->v 的⼀条边，权值为 w
int v = t.first, w = t.second;
if(!st[v])
{
dfs(v);
}
}
}
int main()
{
cin >> n >> m; // 读⼊结点个数以及边的个数
for(int i = 1; i <= m; i++)
{
int a, b, c; cin >> a >> b >> c;
// a 和 b 之间有⼀条边，权值为 c
edges[a].push_back({b, c});
// 如果是⽆向边，需要反过来再存⼀下
edges[b].push_back({a, c});
}
return 0;
}

---

3. ⽤链式前向星的⽅式存储

代码实现：

#include <iostream>
#include <queue>
using namespace std;
const int N = 1e5 + 10;
// 链式前向星
int h[N], e[N * 2], ne[N * 2], w[N * 2], id;
int n, m;
// 其实就是把 b 头插到 a 所在的链表后⾯
void add(int a, int b, int c)
{
id++;
e[id] = b;
w[id] = c; // 多存⼀个权值信息
ne[id] = h[a];
h[a] = id;
}
bool st[N];
void dfs(int u)
{
cout << u << endl;
st[u] = true;
for(int i = h[u]; i; i = ne[i])
{
// u->v 的⼀条边
int v = e[i];
if(!st[v])
{
dfs(v);
}
}
}
int main()
{
cin >> n >> m; // 读⼊结点个数以及边的个数
for(int i = 1; i <= m; i++)
{
int a, b, c; cin >> a >> b >> c;
// a 和 b 之间有⼀条边，权值为 c
add(a, b, c); add(b, a, c);
}
return 0;
}

---

2.5 BFS

和树的遍历⽅式⼀模⼀样，⼀层⼀层的剥开我的⼼~

1. ⽤邻接矩阵的⽅式存储

代码实现：

#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 1010;
int n, m;
int edges[N][N];
bool st[N]; // 标记哪些点已经访问过
void bfs(int u)
{
queue<int> q;
q.push(u);
st[u] = true;
while(q.size())
{
auto a = q.front(); q.pop();
cout << a << endl;
for(int b = 1; b <= n; b++)
{
if(edges[a][b] != -1 && !st[b])
{
q.push(b);
st[b] = true;
}
}
}
}
int main()
{
memset(edges, -1, sizeof edges);
cin >> n >> m; // 读⼊结点个数以及边的个数
for(int i = 1; i <= m; i++)
{
int a, b, c; cin >> a >> b >> c;
// a - b 有⼀条边，权值为 c
edges[a][b] = c;
// 如果是⽆向边，需要反过来再存⼀下
edges[b][a] = c;
}
return 0;
}

---

2. ⽤ vector 数组的⽅式存储

代码实现：

#include <iostream>
#include <vector>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e5 + 10;
int n, m;
vector<PII> edges[N];
bool st[N]; // 标记哪些点已经访问过
void bfs(int u)
{
queue<int> q;
q.push(u);
st[u] = true;
while(q.size())
{
auto a = q.front(); q.pop();
cout << a << endl;
for(auto& t : edges[a])
{
int b = t.first, c = t.second;
if(!st[b])
{
q.push(b);
st[b] = true;
}
}
}
}
int main()
{
cin >> n >> m; // 读⼊结点个数以及边的个数
for(int i = 1; i <= m; i++)
{
int a, b, c; cin >> a >> b >> c;
// a 和 b 之间有⼀条边，权值为 c
edges[a].push_back({b, c});
// 如果是⽆向边，需要反过来再存⼀下
edges[b].push_back({a, c});
}
return 0;
}

---

3. ⽤链式前向星的⽅式存储

代码实现：

#include <iostream>
#include <queue>
using namespace std;
const int N = 1e5 + 10;
// 链式前向星
int h[N], e[N * 2], ne[N * 2], w[N * 2], id;
int n, m;
// 其实就是把 b 头插到 a 所在的链表后⾯
void add(int a, int b, int c)
{
id++;
e[id] = b;
w[id] = c; // 多存⼀个权值信息
ne[id] = h[a];
h[a] = id;
}
bool st[N];
void bfs(int u)
{
queue<int> q;
q.push(u);
st[u] = true;
while(q.size())
{
auto a = q.front(); q.pop();
cout << a << endl;
for(int i = h[a]; i; i = ne[i])
{
int b = e[i], c = w[i];
if(!st[b])
{
q.push(b);
st[b] = true;
}
}
}
}
int main()
{
cin >> n >> m; // 读⼊结点个数以及边的个数
for(int i = 1; i <= m; i++)
{
int a, b, c; cin >> a >> b >> c;
// a 和 b 之间有⼀条边，权值为 c
add(a, b, c); add(b, a, c);
}
return 0;
}

---

3. 最⼩⽣成树

通过前⽂的学习知道，⼀个具有 个顶点的连通图，其⽣成树为包含 条边和所有顶点的极⼩
连通⼦图。对于⽣成树来说，若砍去⼀条边就会使图不连通图；若增加⼀条边就会形成回路。

---

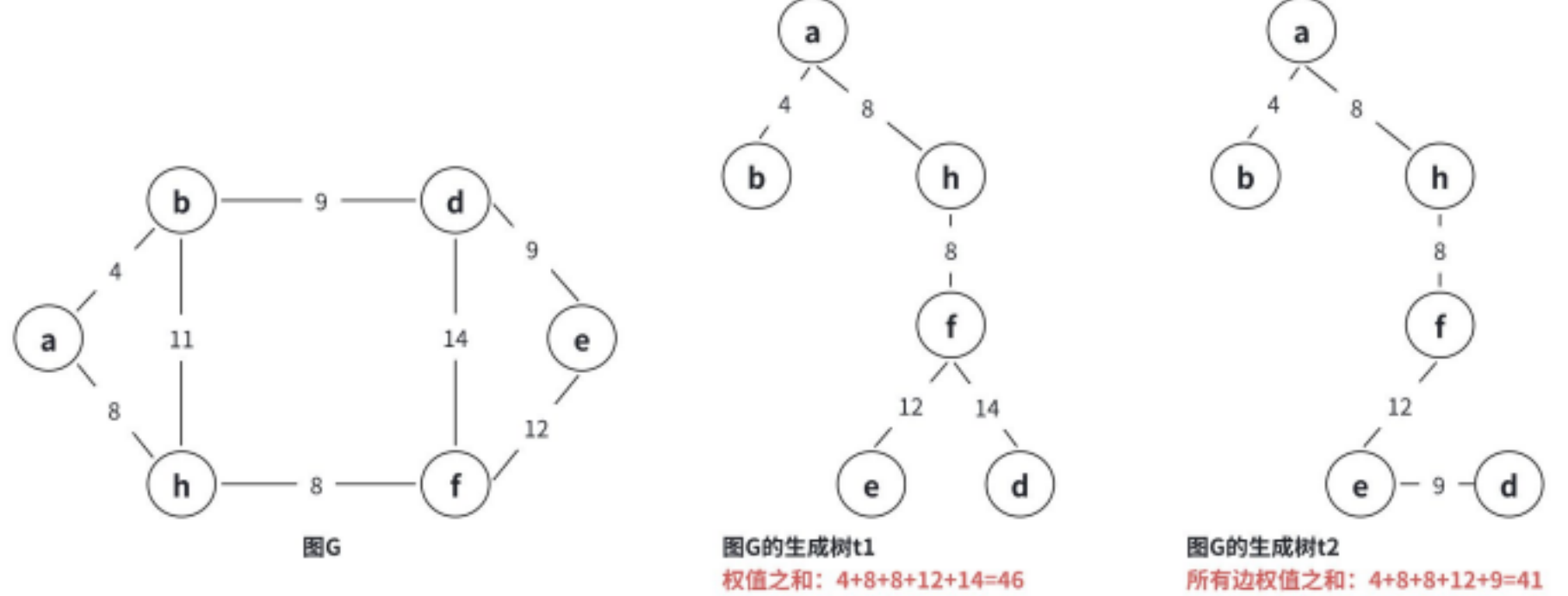
⼀个图的⽣成树可能有多个，将所有⽣成树中权值之和最⼩的树称为最⼩⽣成树。
构造最⼩⽣成树有多种算法，典型的有 普利姆 (Prim) 算法和克鲁斯卡尔 (Kruskal) 算法两种 ，它们都 是基于贪⼼的策略。下⾯讲解算法的具体流程，关于正确性的证明，有兴趣的同学可以看看《算法导 论》中的讲解。

---

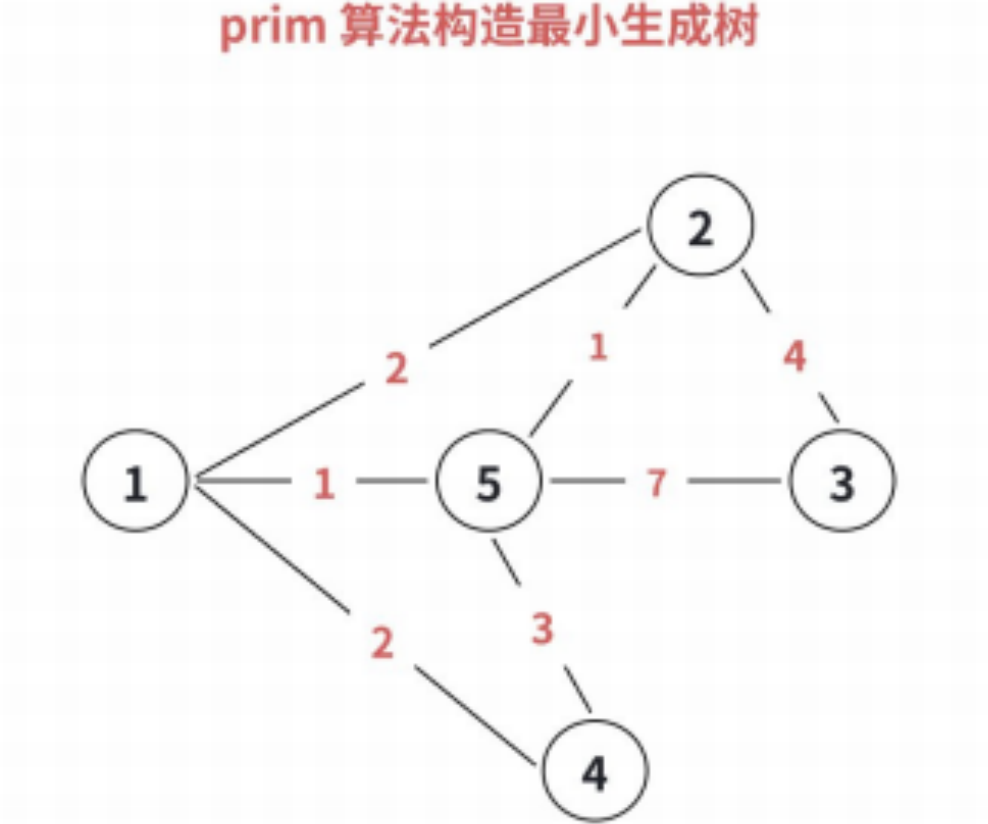
3.1 Prim 算法

核⼼：不断加点。
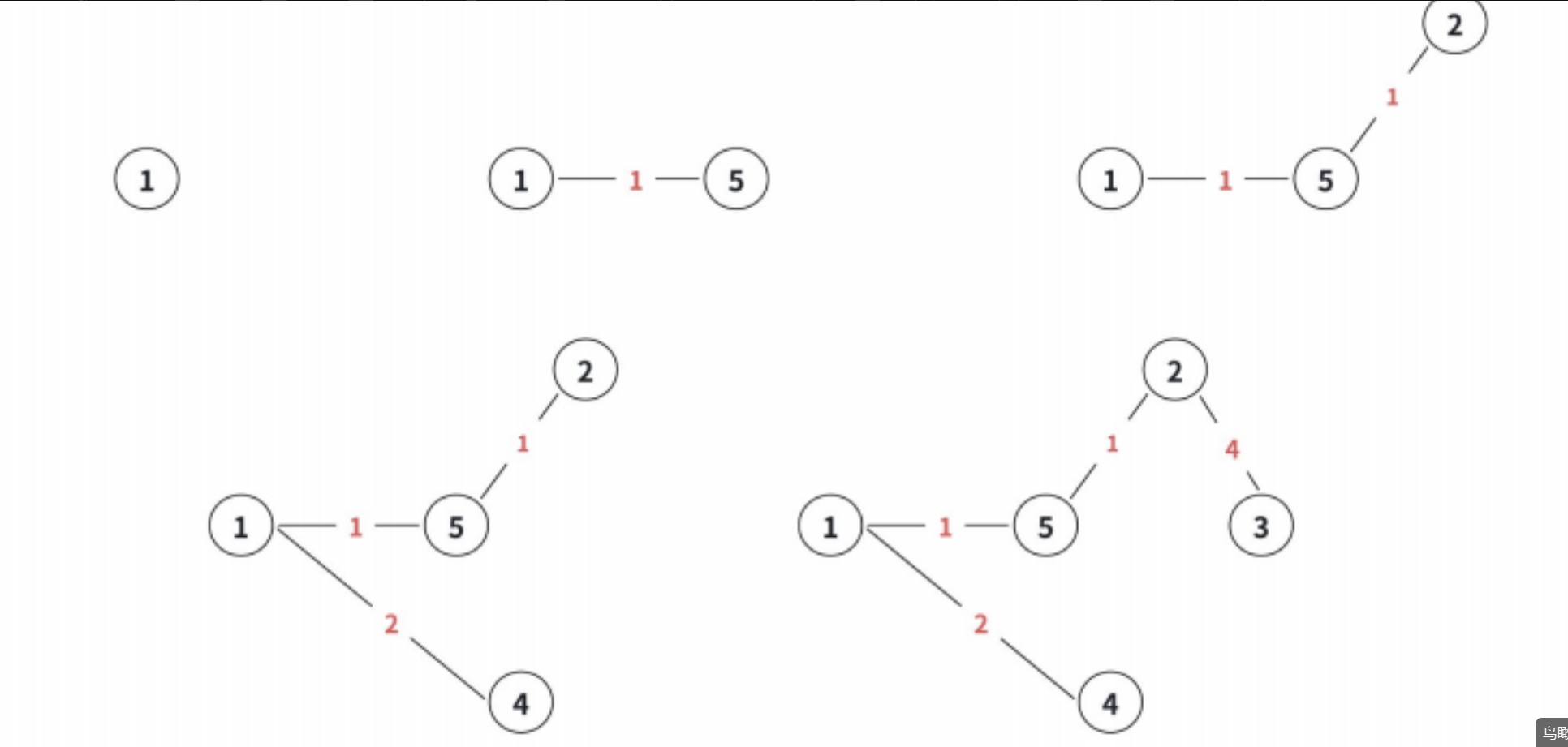
Prim 算法构造最⼩⽣成树的基本思想：
1. 从任意⼀个点开始构造最⼩⽣成树；
2. 将距离该树权值最⼩且不在树中的顶点，加⼊到⽣成树中。然后更新与该点相连的点到⽣成树的最 短距离；
3. 重复 2 操作 n 次，直到所有顶点都加⼊为⽌

---

---

代码实现 - 邻接矩阵：

#include <iostream>
#include <cstring>
using namespace std;
const int N = 5010, INF = 0x3f3f3f3f;
int n, m;
int edges[N][N]; // 邻接矩阵存储图
int dist[N]; // 某个点距离⽣成树的最短距离
bool st[N]; // 标记哪些点已经加⼊到⽣成树
int prim()
{
// 初始化
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
int ret = 0;
for(int i = 1; i <= n; i++) // 循环加⼊ n 个点
{
// 1. 找最近点
int t = 0;
for(int j = 1; j <= n; j++)
if(!st[j] && dist[j] < dist[t])
t = j;
// 判断是否联通
if(dist[t] == INF) return INF;
st[t] = true;
ret += dist[t];
// 2. 更新距离
for(int j = 1; j <= n; j++) // 枚举 t 能⾛到哪
dist[j] = min(dist[j], edges[t][j]);
}
return ret;
}
int main()
{
cin >> n >> m;
// 初始化 邻接矩阵
memset(edges, 0x3f, sizeof edges);
for(int i = 1; i <= m; i++)
{
int x, y, z; cin >> x >> y >> z;
// 注意有重边的情况
edges[x][y] = edges[y][x] = min(edges[x][y], z);
}
int ret = prim();
if(ret == INF) cout << "orz" << endl;
else cout << ret << endl;
return 0;
}

---

代码实现 - 邻接表 - vector 数组：

#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
typedef pair<int, int> PII;
const int N = 5010, INF = 0x3f3f3f3f;
int n, m;
vector<PII> edges[N];
int dist[N];
bool st[N];
int prim()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
int ret = 0;
for(int i = 1; i <= n; i++)
{
// 1. 找最近点
int t = 0;
for(int j = 1; j <= n; j++)
if(!st[j] && dist[j] < dist[t])
t = j;
// 判断是否联通
if(dist[t] == INF) return INF;
st[t] = true;
ret += dist[t];
// 2. 更新距离
for(auto& p : edges[t])
{
int a = p.first, b = p.second;
// t->a 权值是 b
dist[a] = min(dist[a], b);
}
}
return ret;
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= m; i++)
{
int x, y, z; cin >> x >> y >> z;
// 如果有重边，怎么办？
edges[x].push_back({y, z});
edges[y].push_back({x, z});
}
int ret = prim();
if(ret == INF) cout << "orz" << endl;
else cout << ret << endl;
return 0;
}

---

3.2 Kruskal 算法

核⼼：不断加边。
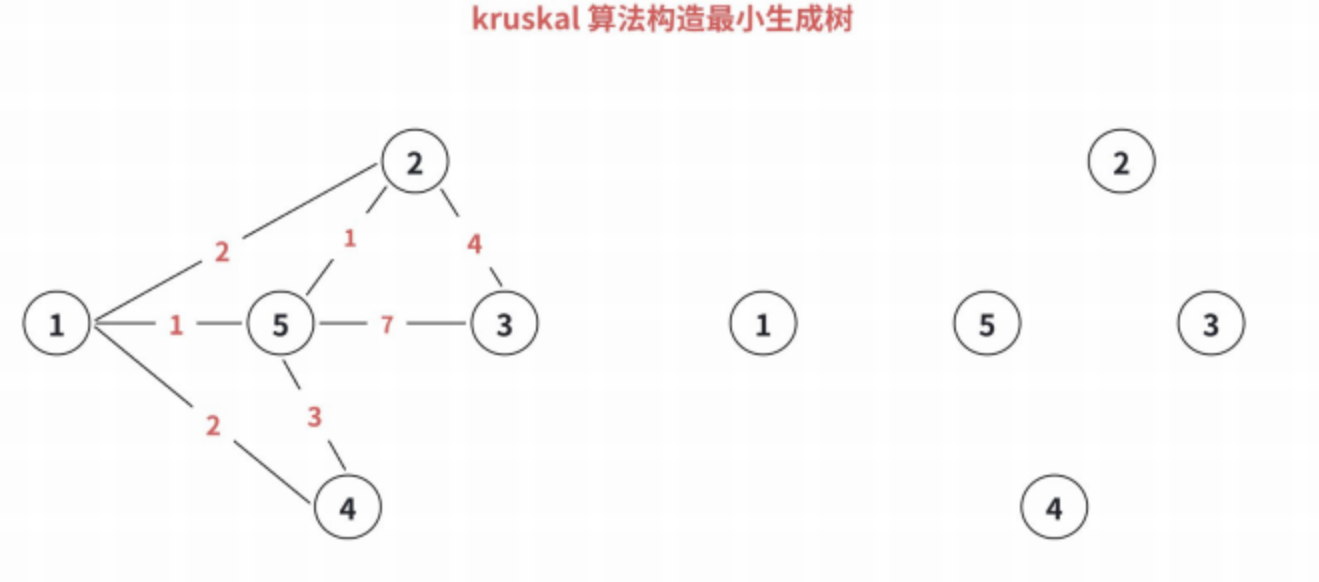
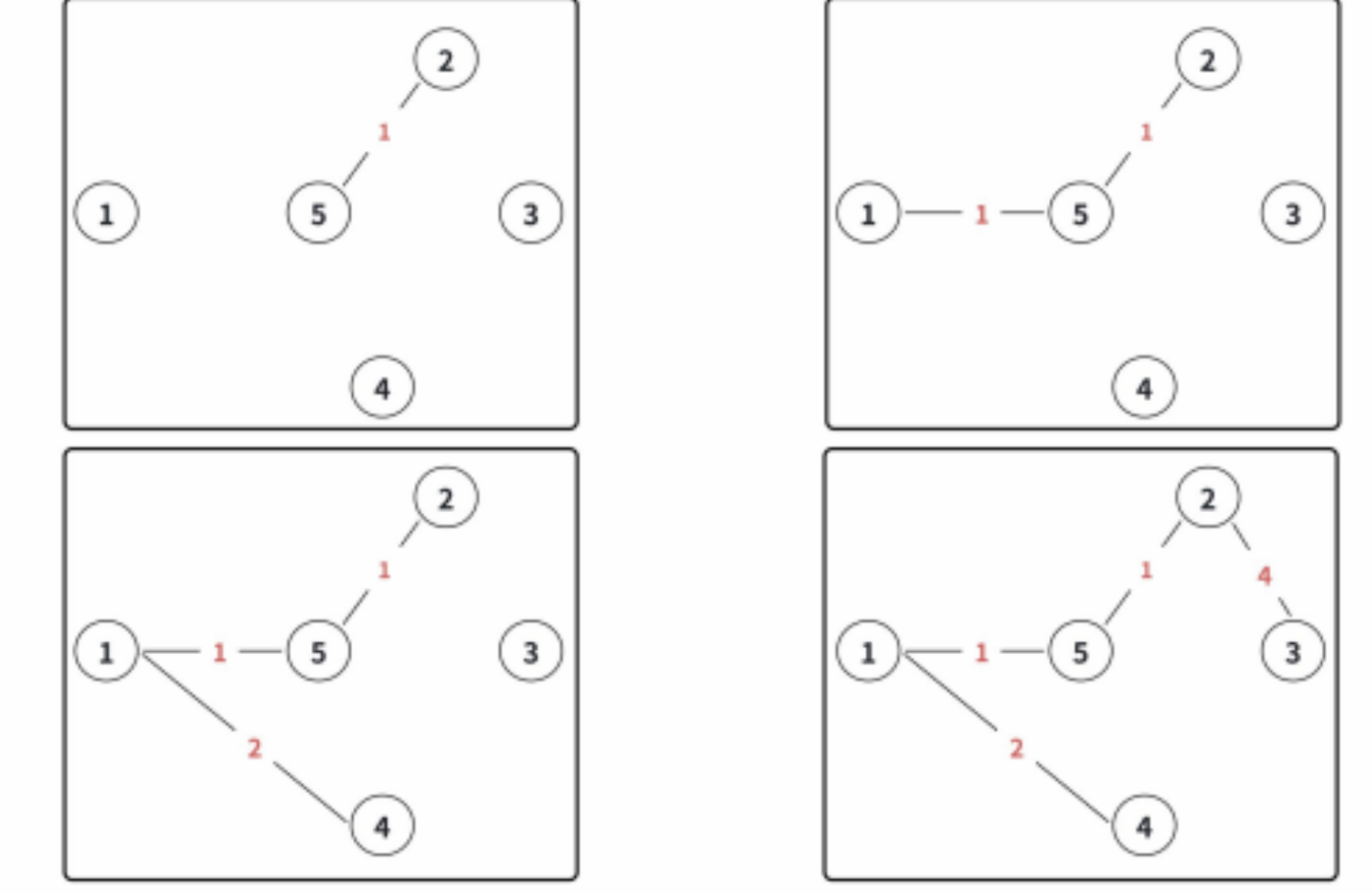
Kruskal 算法构造最⼩⽣成树的基本思想：

1. 所有边按照权值排序；
2. 每次选出权值最⼩且两端顶点不连通的⼀条边，直到所有顶点都联通。

---

---

---

代码实现：

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 5010, M = 2e5 + 10, INF = 0x3f3f3f3f;
int n, m;
struct node
{
int x, y, z;
}a[M];
int fa[N]; // 并查集
bool cmp(node& a, node& b)
{
return a.z < b.z;
}
int find(int x)
{
return x == fa[x] ? fa[x] : fa[x] = find(fa[x]);
}
int kk()
{
sort(a + 1, a + 1 + m, cmp);
int cnt = 0;
int ret = 0;
for(int i = 1; i <= m; i++)
{
int x = a[i].x, y = a[i].y, z = a[i].z;
int fx = find(x), fy = find(y);
if(fx != fy)
{
cnt++;
ret += z;
fa[fx] = fy;
}
}
return cnt == n - 1 ? ret : INF;
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= m; i++) cin >> a[i].x >> a[i].y >> a[i].z;
// 初始化并查集
for(int i = 1; i <= n; i++) fa[i] = i;
int ret = kk();
if(ret == INF) cout << "orz" << endl;
else cout << ret << endl;
return 0;
}

---

3.3 【模板】最⼩⽣成树

题⽬来源： 洛⾕
题⽬链接： P3366 【模板】最⼩⽣成树
难度系数： ★★

题目描述

如题，给出一个无向图，求出最小生成树，如果该图不连通，则输出 orz。

输入格式

第一行包含两个整数 N,M，表示该图共有 N 个结点和 M 条无向边。

接下来 M 行每行包含三个整数 Xi​,Yi​,Zi​，表示有一条长度为 Zi​ 的无向边连接结点 Xi​,Yi​。

输出格式

如果该图连通，则输出一个整数表示最小生成树的各边的长度之和。如果该图不连通则输出 orz。

输入输出样例

输入 #1复制

4 5
1 2 2
1 3 2
1 4 3
2 3 4
3 4 3

输出 #1复制

7

说明/提示

数据规模：

对于 20% 的数据，N≤5，M≤20。

对于 40% 的数据，N≤50，M≤2500。

对于 70% 的数据，N≤500，M≤104。

对于 100% 的数据：1≤N≤5000，1≤M≤2×105，1≤Zi​≤104，1≤Xi​,Yi​≤N。

样例解释：

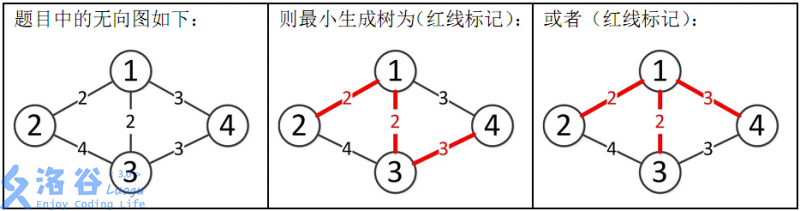
所以最小生成树的总边权为 2+2+3=7。

---

解法：

参考前两个板块⾥⾯的代码。

---

【参考代码】

#include<iostream>
#include<cstring>
using namespace std;

// 常量：N是最大顶点数，INF是无穷大（代表两点没边）
const int N=5050,INF=0x3f3f3f3f;
int n,m;                // n=顶点数（城市数），m=边数（公路数）
int edges[N][N];        // 邻接矩阵：存两个城市之间修路的花费
int dist[N];            // 未连入生成树的城市，到已连城市群的最短距离
bool st[N];             // 标记城市是否已连入生成树

// Prim算法：计算最小生成树的总花费，连不通返回INF
int prim()
{
    // 初始化：所有城市到已连群的距离设为无穷大
    memset(dist,0x3f,sizeof dist);
    dist[1] = 0;        // 选1号城市当起点，到自己的距离是0
    int ret = 0;        // 总花费，初始为0

 
    for(int i=1;i<=n;i++)
    {
        int t=0;
        // 找"没连入"且"离已连群最近"的城市t
        for(int j=1;j<=n;j++)
        {
            if(!st[j] && dist[j]<dist[t])
            {
                t=j;
            }
        }

        // 如果t的距离是无穷大，说明有城市连不通，返回INF
        if(dist[t]==INF) return INF;
        st[t] = true;    // 把t连入生成树
        ret += dist[t];  // 总花费加上连t的花费

        // 更新其他城市到已连群的距离（加入t后可能变近）
        for(int j=1;j<=n;j++)
        {
            dist[j] = min(dist[j], edges[t][j]);
        }
    }
    return ret;
}

int main()
{
    cin >> n >> m;      // 输入城市数n和公路数m
    // 初始化：所有城市之间初始没公路，花费设为无穷大
    memset(edges,0x3f,sizeof edges);

   
    for(int i=1;i<=m;i++)
    {
        int x,y,z;
        cin >> x >> y >> z; // 输入：城市x、城市y、修路花费z
        // 无向图：x到y和y到x的花费一样；有重边选花费最小的
        edges[x][y] = edges[y][x] = min(edges[x][y], z);
    }

    int ret = prim();   // 调用Prim算总花费
    // 输出结果：连不通输出orz，否则输出总花费
    if(ret==INF) cout << "orz" << endl;
    else cout << ret << endl;

    return 0;
}

---

3.4 买礼物

题⽬来源： 洛⾕
题⽬链接： P1194 买礼物
难度系数： ★★

---

题目描述

又到了一年一度的明明生日了，明明想要买 B 样东西，巧的是，这 B 样东西价格都是 A 元。

但是，商店老板说最近有促销活动，也就是：

如果你买了第 I 样东西，再买第 J 样，那么就可以只花 KI,J​ 元，更巧的是，KI,J​ 竟然等于 KJ,I​。

现在明明想知道，他最少要花多少钱。

输入格式

第一行两个整数，A,B。

接下来 B 行，每行 B 个数，第 I 行第 J 个为 KI,J​。

我们保证 KI,J​=KJ,I​ 并且 KI,I​=0。

特别的，如果 KI,J​=0，那么表示这两样东西之间不会导致优惠。

注意 KI,J​ 可能大于 A。

输出格式

一个整数，为最小要花的钱数。

输入输出样例

输入 #1复制

1 1
0

输出 #1复制

1

输入 #2复制

3 3
0 2 4
2 0 2
4 2 0

输出 #2复制

7

说明/提示

样例解释 2。

先买第 2 样东西，花费 3 元，接下来因为优惠，买 1,3 样都只要 2 元，共 7 元。

（同时满足多个"优惠"的时候，聪明的明明当然不会选择用 4 元买剩下那件，而选择用 2 元。）

数据规模

对于 30% 的数据，1≤B≤10。

对于 100% 的数据，1≤B≤500,0≤A,KI,J​≤1000。

2018.7.25新添数据一组

---

【解法】

题⽬转化：
• 如果把每⼀个零⻝看成⼀个节点，优惠看成⼀条边，就变成在图中找最⼩⽣成树的问题。
• 因此，跑⼀遍 kk 算法即可。

---

【参考代码】

#include <iostream>
#include <algorithm>
using namespace std;

// 常量：最多的边数（B最多500，所以边数最多500×500/2=125000，N设大一点）
const int N = 500 * 500 + 10;

int a, n;        // a=原价A，n=要买的东西数量B
int pos;         // 记录有效优惠边的数量（边的计数器）

// 边的结构体：x和y是两个顶点（东西），z是优惠价K[x][y]
struct node
{
    int x, y, z;
}e[N];

int fa[N];       // 并查集数组：用来判断两个顶点是否连通（避免选环）

// 并查集查找函数（找顶点x的根节点，带路径压缩，更快）
int find(int x)
{
    return fa[x] == x ? x : fa[x] = find(fa[x]);
}

int cnt, ret;    // cnt=选的优惠边数，ret=选的优惠边总权值

// 排序规则：按边的权值从小到大排（Kruskal核心：选最便宜的边）
bool cmp(node& a, node& b)
{
    return a.z < b.z;
}

// Kruskal算法核心函数：选最小边构建生成树
void kk()
{
    // 第一步：把所有有效边按权值从小到大排序
    sort(e + 1, e + 1 + pos, cmp);
    
    // 第二步：遍历所有边，选不构成环的边
    for(int i = 1; i <= pos; i++)
    {
        int x = e[i].x, y = e[i].y, z = e[i].z; // 取当前边的两个顶点和权值
        int fx = find(x), fy = find(y);         // 找x和y的根节点
        
        if(fx != fy) // 根节点不同→不连通→选这条边（不会构成环）
        {
            cnt++;          // 优惠边数+1
            ret += z;       // 总优惠权值+当前边的权值
            fa[fx] = fy;    // 把x和y连通（合并集合）
        }
    }
}

int main()
{
    cin >> a >> n; // 输入原价a，东西数量n（对应题目里的A、B）
    
    // 读入B×B的优惠矩阵K[I][J]
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= n; j++)
        {
            int k; cin >> k; // 读入K[i][j]
            
            // 过滤无效边：
            // 1. i>=j：避免重复（K[i][j]=K[j][i]，只存i<j的）；
            // 2. k>a：优惠价比原价贵，没必要选；
            // 3. k==0：无优惠，跳过；
            if(i >= j || k > a || k == 0) continue;
            
            pos++; // 有效边数+1
            e[pos].x = i; e[pos].y = j; e[pos].z = k; // 存这条边
        }
    }
    
    // 初始化并查集：每个顶点的根节点是自己
    for(int i = 1; i <= n; i++) fa[i] = i;
    
    // 调用Kruskal算法选优惠边
    kk();
    
    // 计算总花费：优惠边总权值 + （总数量-优惠边数）×原价
    cout << ret + (n - cnt) * a << endl;
    
    return 0;
}

---

3.5 繁忙的都市

题⽬来源： 洛⾕
题⽬链接： P2330 [SCOI2005] 繁忙的都市
难度系数： ★★

---

题目描述

城市 C 是一个非常繁忙的大都市，城市中的道路十分的拥挤，于是市长决定对其中的道路进行改造。城市 C 的道路是这样分布的：城市中有 n 个交叉路口，有些交叉路口之间有道路相连，两个交叉路口之间最多有一条道路相连接。这些道路是双向的，且把所有的交叉路口直接或间接的连接起来了。每条道路都有一个分值，分值越小表示这个道路越繁忙，越需要进行改造。但是市政府的资金有限，市长希望进行改造的道路越少越好，于是他提出下面的要求：

1. 改造的那些道路能够把所有的交叉路口直接或间接的连通起来。
2. 在满足要求 1 的情况下，改造的道路尽量少。
3. 在满足要求 1、2 的情况下，改造的那些道路中分值最大的道路分值尽量小。

任务：作为市规划局的你，应当作出最佳的决策，选择哪些道路应当被修建。

输入格式

第一行有两个整数 n,m 表示城市有 n 个交叉路口，m 条道路。

接下来 m 行是对每条道路的描述，u,v,c 表示交叉路口 u 和 v 之间有道路相连，分值为 c。

输出格式

两个整数 s,max，表示你选出了几条道路，分值最大的那条道路的分值是多少。

输入输出样例

输入 #1复制

4 5
1 2 3
1 4 5
2 4 7
2 3 6
3 4 8

输出 #1复制

3 6

说明/提示

数据范围及约定

对于全部数据，满足 1≤n≤300，1≤c≤104，1≤m≤8000。

---

【解法】

定理：最⼩⽣成树就是瓶颈⽣成树。
在 kk 算法中，维护边权的最⼤值即可。

---

【参考代码】

#include <iostream>
#include <algorithm>
using namespace std;

// 常量：N=路口数上限（310），M=道路数上限（8010）
const int N = 310, M = 8010;

int n, m;        // n=路口数，m=道路数
struct node      // 道路结构体：x/y是两个路口，z是分值
{
    int x, y, z;
}e[M];

int fa[N];       // 并查集数组：判断两个路口是否连通（避免选环）
int ret;         // 记录最小生成树中"分值最大的边"的分值

// 并查集查找函数（找根节点，带路径压缩，更快）
int find(int x)
{
    return fa[x] == x ? x : fa[x] = find(fa[x]);
}

// 排序规则：按道路分值从小到大排（Kruskal核心：选最便宜/最需要改造的边）
bool cmp(node& a, node& b)
{
    return a.z < b.z;
}

// Kruskal算法核心：构建最小生成树，记录最大边的分值
void kk()
{
    // 初始化并查集：每个路口的根节点是自己
    for(int i = 1; i <= n; i++) fa[i] = i;
    
    // 第一步：把所有道路按分值从小到大排序
    sort(e + 1, e + 1 + m, cmp);
    
    // 第二步：遍历排序后的道路，选不构成环的边（构建最小生成树）
    for(int i = 1; i <= m; i++)
    {
        int x = e[i].x, y = e[i].y, z = e[i].z; // 取当前道路的两个路口和分值
        int fx = find(x), fy = find(y);         // 找x和y的根节点
        
        if(fx != fy) // 根节点不同→不连通→选这条边（不会构成环）
        {
            ret = max(ret, z); // 更新"最大分值"（选的边里最大的z）
            fa[fx] = fy;       // 把x和y连通（合并集合）
        }
    }
}

int main()
{
    cin >> n >> m; // 输入路口数n，道路数m
    
    // 读入m条道路的信息
    for(int i = 1; i <= m; i++) cin >> e[i].x >> e[i].y >> e[i].z;
    
    // 改造的道路数固定是n-1（生成树边数），先输出
    cout << n - 1 << " ";
    
    // 调用Kruskal算法，找最小生成树的最大边分值
    kk();
    
    // 输出最大分值
    cout << ret << endl;
    
    return 0;
}

---