【数据结构】排序算法精讲｜折半插入排序全解：高效优化、性能对比、实战剖析

蒙奇D索大2025-12-27 9:56

折半插入排序

导读

大家好，很高兴又和大家见面啦！！！

在上一篇内容中我们知道了 排序 的基本定义：

  • 重新排列表中的元素，使表中的元素满足按关键字有序的过程。

排序算法我们按数据元素是否完全存放在内存中，将其分为了两大类：

  • 内部排序：排序期间元素全部存放在内存中的排序
  • 外部排序：排序期间元素无法全部同时存放在内存中，必须在排序的过程中根据要求不断地在内、外存之间移动的排序

内部排序算法又可以根据其具体实现方式分为两大类：

  • 比较排序：需要通过元素之间的比较，确定对应元素的前后关系的排序
  • 非比较排序：不需要通过元素之间的比较，就能确定对应元素的前后关系的排序

上一篇内容中我们介绍了比较排序中的第一类排序------插入排序 ；

插入排序 作为一种简单直观的排序算法，其 基本思想 是：

  • 每次将一个待排序的记录按其关键字大小插入到前面已排好序的子序列中，直到全部记录插入完成。

直接插入排序 就是严格按照该思想完成的最简单也最直观的排序算法。但是由于每一次的插入过程都需要将待排序元素与已经有序的子序列中的元素依次比较，这就带来了巨大的时间消耗。因此 直接插入排序 的 算法性能 在平均情况下 时间复杂度 都能达到 O ( N 2 ) \bm{O(N^2)} O(N2) 这个数量级。

&bnsp;

那有没有一种更优的 插入排序算法 呢？

&bnsp;

答案是肯定的。在今天的内容中，我将会介绍 直接插入排序 的第一种优化方式------折半插入排序 。

下面就让我们一起进入今天的内容吧！！！

一、优化思路分析

按照 插入排序 的算法思想，直接插入排序 我可以将其分为 三部分：
有序子序列
待排序元素
无序子序列

每一次的元素插入过程实际上就是 在有序子序列中查找待排序元素的位置 ，那也就是说 直接插入排序 的过程我们可以将其视为三步：

  • 查找 ：在有序子序列中通过 比较操作 查找待排序元素的位置
  • 移动 ：在 查找 的过程中通过 移动操作 为该元素腾出位置
  • 插入 ：在找到待排序元素的位置后直接 插入 该元素

若我们想要对 直接插入排序 进行优化，那么我们必然就需要从这三步出发；

由于 移动操作 以及 插入操作 已经是效率最高的实现方式，因此我们只能从 查找操作 入手，通过优化 查找 的过程，从而优化整个 插入排序算法 ；

查找 的优化相信大家都不陌生了，在上一个章节中，我们介绍了一系列的 查找算法，现在就是我们学以致用的时候了；

二、查找优化

在 查找 篇章中我们有介绍过，对于有序的顺序表 ，我们可以通过 折半查找 来提高 查找 的效率；

而 直接插入排序 的对象既可以是 顺序表 也可以是 链表 ，因此，当我们对 顺序表 进行 直接插入排序 时，我们就可以考虑通过 折半查找 在 有序的子序列 中 查找 待排序元素需要 插入 的位置；

这种在 顺序表 中将 折半查找 与 插入排序 相结合的 排序算法 就是我们今天要介绍的 折半插入排序；

三、算法思想

折半插入排序 的 算法思想 与 直接插入排序 的算法思想基本一致，它们之间的区别就是在 查找 上，其具体内容如下所示：

  • 将排序对象划分为三部分
    • 左侧有序子序列
    • 待排序元素
    • 右侧无序子序列
  • 记录待排序元素的数据信息
  • 在左侧有序子序列中 通过折半查找 ，找到待排序对象的位置
  • 按排序对象在左侧有序子序列中的位置插入待排序元素
  • 重复上述步骤，直到右侧无序子序列中的所有元素均完成排序

折半插入排序 的 算法思想 用一句话概括就是：

  • 先用折半查找找到应该插入的位置，再插入元素

不过要注意的是，直接插入排序 在 顺序查找 的过程中，就一并完成了 移动操作 ，但是在 折半插入排序 中，我们需要 先查找，再整体右移 ；

由于 折半插入排序 是 折半查找算法 与 插入排序算法 的组合应用，因此该算法仅适用于顺序表 ；

接下来，我们就来一起通过 C语言 实现 折半插入排序；

四、C语言实现

4.1 准备工作

在实现 折半插入排序 之前，我们需要先创建好三个文件：

  • 排序算法头文件 Binary_Insertion_Sort.h ------ 用于进行排序算法的声明
  • 排序算法实现文件 Binary_Insertion_Sort.c ------ 用于实现排序算法
  • 排序算法测试文件 text.c ------ 用于测试排序算法

4.2 函数三要素

与 直接插入排序 一样，折半插入排序 只不过是在其基础上对查找操作进行了优化，因此我们这里的三要素只需要修改一下函数名即可：

c 复制代码 
// 插入排序------折半插入排序
void BInsertSort(ElemType* nums, int len) {

}

4.3 排序对象的划分

折半插入排序 同样是将 排序对象 划分为 三部分：

  • 左侧有序
  • 待排序对象
  • 右侧无序

不过由于今天我们需要实现 折半查找 ，因此我们还需要在这个基础上进一步的进行划分：
右侧无序
左边界
中间无序元素
右边界
左侧有序
左边界
中间有序元素
右边界
待排序对象

如上图所示，这里我们进一步的将 左侧有序 以及 右侧无序 按其边界进一步划分出来了 左右边界 ；

由于 折半查找 是发生在 左侧有序 ，因此我们这里则是以 左侧有序的右边界 为分界点，将排序对象进行划分：

c 复制代码 
	// 按左侧有序有边界进行划分
	for (int i = 0; i < len - 1; i++) {
		int key = nums[i + 1];	// 待排序对象
	}

4.4 插入位置查找

在 折半插入排序 中，我们对 待排序对象 的插入位置进行 查找 时，采用的是 折半查找 ，因此其具体实现如下所示：

c 复制代码 
		// 折半查找
		int l = 0, r = i;	// 折半查找的左右指针
		while (l <= r) {
			int m = (r - l) / 2 + l;
			// 中间值 大于 目标值，目标值位于中间值左侧
			if (nums[m] > key) {
				r = m - 1;	// 更新右边界
			}
			// 中间值 小于等于 目标值，目标值位于中间值右侧
			else {
				l = m + 1;
			}
		}

因为前面我们采用的是 左侧有序的右边界 作为分界线，因此在进行 查找操作 时，分界线 i 就是 折半查找 的 右边界 ；

查找的具体过程这里我就不再多加赘述，不熟悉 折半查找 的朋友们可以点击链接回顾一下其具体内容；

4.5 待排序对象的插入

这里需要注意的是，折半查找 的过程不进行 移动操作 ，因此我们在找到其具体位置后，我们需要先将该位置通过 移动操作 给空出来，随后再进行插入操作：

c 复制代码 
		// 移动
		for (int j = i; j >= l; j--) {
			nums[j + 1] = nums[j];
		}
		// 插入
		nums[l] = key;

这里有朋友可能会奇怪为什么是 l 这个点为 插入位置 ，而不是 r ，这是因为 插入排序 是一个 稳定排序算法 ，因此对于 值相同 的元素，该排序算法并不会改变它们之间的位置；并且我们是从左侧开始进行排序，因此当我们找到一个相同元素时，待插入元素一定位于其右侧；

在进行 移动时 我们是从 左侧有序 的右边界出发，依次将元素向后移动，直到 l 指向的位置被空出来为止，因此我们是从 i 开始，到 l 结束；

由于 折半插入排序 仅适用于 顺序表 ，因此当我们找到了 待排序对象 的 插入位置 后，我们只需要通过 赋值 操作即可实现插入：

4.6 时间复杂度分析

在 折半插入排序 中，主要耗时的有三个操作：

  • 顺序查找 ：从左侧开始 顺序查找 待排序对象，该操作的 时间复杂度 为 O ( N ) O(N) O(N)
  • 折半查找 ：从 左侧有序子序列 中 折半查找 插入位置，该操作的 时间复杂度 为 O ( log ⁡ N ) O(\log N) O(logN)
  • 顺序移动 ：从 左侧有序子序列 的右边界开始 顺序移动 元素，该操作的 时间复杂度 为 O ( N ) O(N) O(N)

因此总的 时间复杂度 为 T ( N ) = O ( N log ⁡ N + N 2 ) = N 2 T(N) = O(N\log N + N^2) = N^2 T(N)=O(NlogN+N2)=N2 ；

当然这里我说的是 平均情况 下的 时间复杂度 ，在 最好情况 和 最坏情况 下的时间复杂度分别为：

  • 最好情况 ： O ( N log ⁡ N ) O(N\log N) O(NlogN) ------ 待排序序列已经有序，但 折半查找 仍需要 O ( log ⁡ N ) O(\log N) O(logN) 的时间
  • 最坏情况 ： O ( N 2 ) O(N^2) O(N2) ------ 待排序序列 逆序排列

这时有朋友可能就会说了，你这比起 直接插入排序 这时间效率上也没有提升啊！为什么说 折半插入排序 是对 直接插入排序 的优化呢？

这个问题我个人认为十分精炼，一下子就切中了要害。这里我给出的解释是：

  • 优化指的是在 查找操作 上的优化：
    • 直接插入排序 的 查找操作 为 顺序查找
    • 折半插入排序 的 查找操作 则是更优的 折半查找
  • 之所以整体效率没有提升，问题出在 移动操作 上
    • 直接插入排序 的 移动操作 同样为 顺序移动 但是该操作是在查找的过程中完成，因此每一次的移动我们都可以视为 O ( 1 ) O(1) O(1)
    • 折半插入排序 的 移动操作 则是一次性完成，因此整体的移动为 O ( N ) O(N) O(N)

当我们将 直接插入排序 中的 查找 与 移动 分割开时，这时的 直接插入排序 就变成了：

  • 顺序查找 ：从左侧开始 顺序查找 待排序对象，该操作的 时间复杂度 为 O ( N ) O(N) O(N)
  • 顺序查找 ：从 左侧有序子序列 中 顺序查找 插入位置，该操作的 时间复杂度 为 O ( N ) O(N) O(N)
  • 顺序移动 ：将 左侧有序子序列 中的元素向右 顺序移动 ，该操作的 时间复杂度 为 O ( N ) O(N) O(N)

此时我们再来看 直接插入排序 总的 时间复杂度 ，现在就变成了：

  • 最好情况 ： T ( N ) = O ( N ∗ 1 + N ∗ 1 ) = O ( N ) T(N) = O(N * 1 + N * 1) = O(N) T(N)=O(N∗1+N∗1)=O(N) ------ 待排序序列已经有序，查找 与 移动 的 时间复杂度 均为 O ( 1 ) O(1) O(1)
  • 最坏情况 ： T ( N ) = O ( N ∗ N + N ∗ N ) = O ( N 2 ) T(N) = O(N * N + N * N) = O(N^2) T(N)=O(N∗N+N∗N)=O(N2) ------ 待排序序列 逆序排列 ，查找 与 移动 的 时间复杂度 均为 O ( 1 ) O(1) O(1)
  • 平均情况 ： T ( N ) = O ( N ∗ N + N ∗ N ) = O ( N 2 ) T(N) = O(N * N + N * N) = O(N^2) T(N)=O(N∗N+N∗N)=O(N2) ------ 查找 与 移动 的 时间复杂度 均为 O ( N ) O(N) O(N)

现在我们就能更直观的感受到 折半插入排序 的优化点是在 查找操作 上的优化；

这里我们还需要明白一件事，虽然 直接插入排序 与 折半插入排序 它们的 时间复杂度 均为 O ( N 2 ) O(N^2) O(N2) 这个级别，但是实际的效率一定是 折半插入排序 的效率更高；

4.7 算法代码

完整代码如下所示：

c 复制代码 
// 算法头文件
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <time.h>
#include <assert.h>

typedef int ElemType;
// 插入排序------折半插入排序
void BInsertSort(ElemType* nums, int len);
// 插入排序------直接插入排序
void InsertSort(ElemType* a, int len);
// 数组打印
void Print(ElemType* arr, int len);
// 折半插入排序测试
void test();

// 算法实现文件
#include "Binary_Insertion_Sort.h"
// 插入排序------折半插入排序
void BInsertSort(ElemType* nums, int len) {
	// 按左侧有序有边界进行划分
	for (int i = 0; i < len - 1; i++) {
		int key = nums[i + 1];	// 待排序对象
		// 折半查找
		int l = 0, r = i;	// 折半查找的左右指针
		while (l <= r) {
			int m = (r - l) / 2 + l;
			// 中间值 大于 目标值，目标值位于中间值左侧
			if (nums[m] > key) {
				r = m - 1;	// 更新右边界
			}
			// 中间值 小于等于 目标值，目标值位于中间值右侧
			else {
				l = m + 1;
			}
		}
		// 移动
		for (int j = i; j >= l; j--) {
			nums[j + 1] = nums[j];
		}
		// 插入
		nums[l] = key;
	}
}

//插入排序------直接插入排序
void InsertSort(ElemType* a, int len) {
	//以左侧有序对象的起点作为分界线对排序对象进行划分
	for (int i = 0; i < len - 1; i++) {
		//记录需要排序的元素
		ElemType key = a[i + 1];
		//插入位置的查找
		int j = i;//记录左侧有序元素的起点
		//j < 0时表示查找完左侧所有元素
		//a[j] <= key时表示找到了元素需要进行插入的位置
		while (j >= 0 && a[j] > key) {
			a[j + 1] = a[j];//元素向后移动
			j -= 1;//移动查找指针
		}
		//插入元素
		a[j + 1] = key;
	}
}

// 数组打印
void Print(ElemType* arr, int len) {
	printf("元素序列：");
	for (int i = 0; i < len; i++) {
		printf("%d\t", arr[i]);
	}
	printf("\n");
}

// 折半插入排序测试
void test() {
	ElemType* arr1 = (ElemType*)calloc(100000, sizeof(ElemType));
	assert(arr1);
	ElemType* arr2 = (ElemType*)calloc(100000, sizeof(ElemType));
	assert(arr2);
	ElemType* arr3 = (ElemType*)calloc(10, sizeof(ElemType));
	assert(arr3);
	// 设置伪随机数
	srand((unsigned)time(NULL));
	// 生成10w个随机数
	for (int i = 0; i < 100000; i++) {
		arr1[i] = rand() % 100000;
		arr2[i] = arr1[i];
		if (i < 10) {
			arr3[i] = rand() % 100;
		}
	}

	// 算法健壮性测试
	printf("\n排序前：");
	Print(arr3, 10);
	BInsertSort(arr3, 10);
	printf("\n排序后：");
	Print(arr3, 10);

	// 算法效率测试
	int begin1 = clock();
	BInsertSort(arr1, 100000);
	int end1 = clock();
	double time_used1 = ((double)(end1 - begin1)) / CLOCKS_PER_SEC;
	printf("\n折半插入排序总耗时：%lf 秒\n", time_used1);

	int begin2 = clock();
	InsertSort(arr2, 100000);
	int end2 = clock();

	double time_used2 = ((double)(end2 - begin2)) / CLOCKS_PER_SEC;
	printf("\n直接插入排序总耗时：%lf 秒\n", time_used2);

	free(arr1);
	arr1 = NULL;
	free(arr2);
	arr2 = NULL;
	free(arr3);
	arr3 = NULL;
}

// 算法测试文件
#include "Binary_Insertion_Sort.h"

int main() {
	test();
	return 0;
}

下面我们就来允许一下代码，简单测试一下：

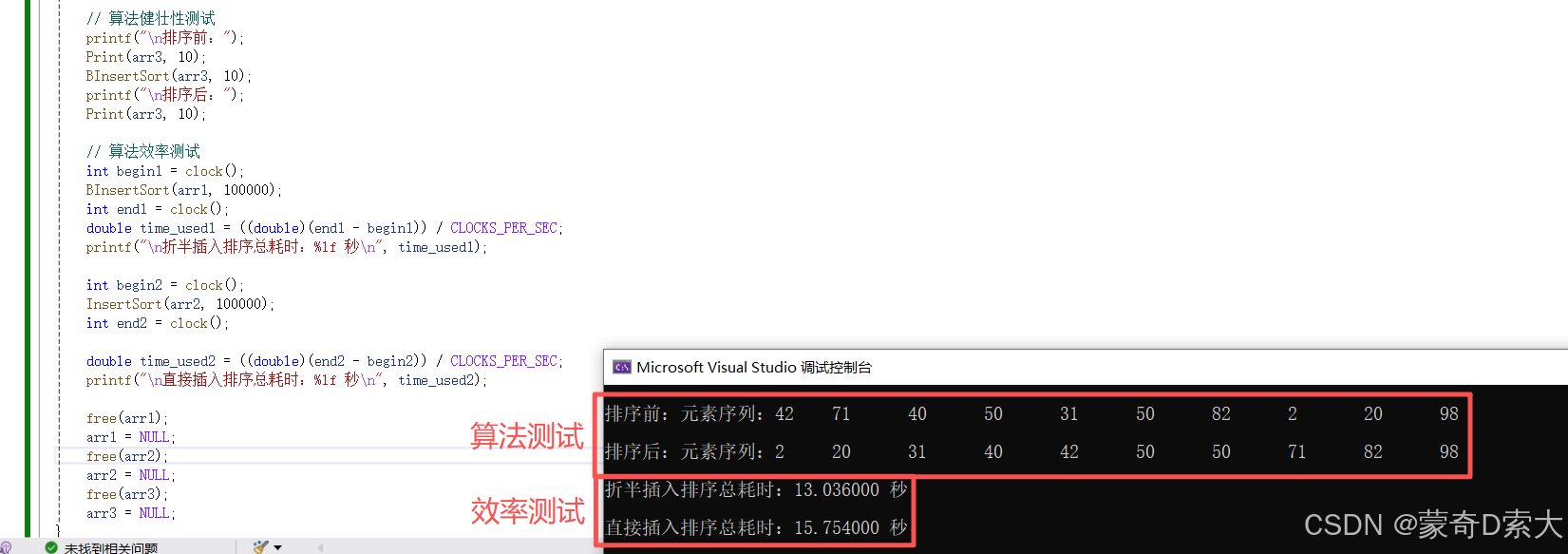
从这次的测试结果中我们可以看到，在 10 w 10w 10w 个数据规模下，两个完全一样的数组通过 折半插入排序 所消耗的时间明显比 直接插入排序 所消耗的时间要少；

结语

在今天的内容中我们详细介绍了 折半插入排序 的 算法思想 和 C语言实现 ；

折半插入排序 就是 折半查找 与 插入排序 相结合的 排序算法 ，其 算法思想 为：

  • 先通过 折半查找 在 左侧有序序列 中找到待插入位置，再将 待插入元素 直接插入到该位置中

折半插入排序 的算法效率虽然与 直接插入排序 的算法效率属于同一个数量级，均为： O ( N 2 ) O(N^2) O(N2) ，但是在实际的使用中，折半插入排序 的效率是明显优于 直接插入排序 的算法效率；

折半插入排序 的 算法实现 就是在 直接插入排序 的基础上，将 查找 与 移动 这两个操作分离开，并直接对 查找 操作进行优化，将其优化为 折半查找 ；

总体来说 折半插入排序 的 算法思想 以及 算法实现 并不复杂，但是与我们所想的算法优化还是有一定的区别。那么有没有更优的 插入排序 呢？

答案是肯定的，在下一篇内容中，我们将会介绍 插入排序 的王者------希尔排序 。大家记得关注哦！！！

互动与分享

  • 点赞👍 - 您的认可是我持续创作的最大动力

  • 收藏⭐ - 方便随时回顾这些重要的基础概念

  • 转发↗️ - 分享给更多可能需要的朋友

  • 评论💬 - 欢迎留下您的宝贵意见或想讨论的话题

感谢您的耐心阅读！ 关注博主，不错过更多技术干货。我们下一篇再见！

相关推荐
有个人神神叨叨2 小时前
odoo 学习- 01. Odoo 工程结构概览
学习
有个人神神叨叨2 小时前
odoo 学习- 02. Odoo 核心框架探究
学习
汽车仪器仪表相关领域2 小时前
ZDT-III 通用电机测试系统
数据库·算法·单元测试·压力测试·可用性测试
石像鬼₧魂石2 小时前
SQLMap注入完整操作流程（含全部细节 靶机学习用）
学习
前端小白在前进2 小时前
力扣刷题：矩阵重叠
算法·leetcode·矩阵
啊阿狸不会拉杆2 小时前
《数字图像处理》-实验1
图像处理·人工智能·算法·计算机视觉·数字图像处理
复业思维202401082 小时前
STM32学习和实践笔记（45）：SPI-FLASH实验
笔记·stm32·学习
2301_781143562 小时前
python学习（一）
python·学习
热门推荐
01从快手“12·22”直播攻击事件看：一次教科书式的业务层饱和攻击02GitHub 镜像站点033D 圣诞树网页代码04Linux下V2Ray安装配置指南05UV安装并设置国内源06电脑检测软件—图吧工具箱07在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）08Gemini3 生成的基于手势控制3D粒子圣诞树09jdk21下载、安装（Windows、Linux、macOS）10Claude Code Skills 实用使用手册