【算法通关指南：数据结构与算法篇】破局二叉树！特殊结构 + 双重存储 + 遍历算法，一文吃透所有核心

🔥小龙报：个人主页

🎬作者简介：C++研发，嵌入式，机器人方向学习者

❄️个人专栏：《算法通关指南》
✨ 永远相信美好的事情即将发生

文章目录

前言
一、二叉树的概念
- [1.1 二叉树的定义](#1.1 二叉树的定义)
- [1.2 特殊的二叉树](#1.2 特殊的二叉树)
- - [1.2.1 满二叉树](#1.2.1 满二叉树)
  - [1.2.2 完全二叉树](#1.2.2 完全二叉树)
二、二叉树的存储
- [2.1 顺序存储](#2.1 顺序存储)
- [2.2 链式存储](#2.2 链式存储)
三、二叉树的遍历
- [3.1 深度优先遍历](#3.1 深度优先遍历)
- - [3.1.1 先序遍历](#3.1.1 先序遍历)
  - [3.1.2 中序遍历](#3.1.2 中序遍历)
  - [3.1.3 后序遍历](#3.1.3 后序遍历)
  - [3.1.4 所有测试代码](#3.1.4 所有测试代码)
- [3.2 宽度优先遍历](#3.2 宽度优先遍历)
总结与每日励志

前言

本专栏聚焦算法题实战，系统讲解算法模块：以《c++编程》，《数据结构和算法》《基础算法》《算法实战》等几个板块以题带点，讲解思路与代码实现，帮助大家快速提升代码能力。
ps:本章节题目分两部分，比较基础笔者只附上代码供大家参考，其他的笔者会附上自己的思考和讲解，希望和大家一起努力见证自己的算法成长

一、二叉树的概念

1.1 二叉树的定义

二叉树是⼀种特殊的树型结构，它的特点是每个结点至多只有2棵子树（即二叉树中不存在度大于2的结点），并且二叉树的子树有左右之分，其次序不能任意颠倒。
二叉的意思是这种树的每⼀个结点最多只有两个孩子结点。注意这里是最多有两个孩子，也可能没有孩子或者是只有一个孩子
注：二叉树结点的两个孩子，⼀个被称为左孩子，⼀个被称为右孩子。其顺序是固定的，就像人的左手和右手，不能颠倒混淆

1.2 特殊的二叉树

1.2.1 满二叉树

⼀棵二叉树的所有非叶子节点都存在左右孩子并且所有叶子节点都在同⼀层上，那么这棵树就称为满二叉树。

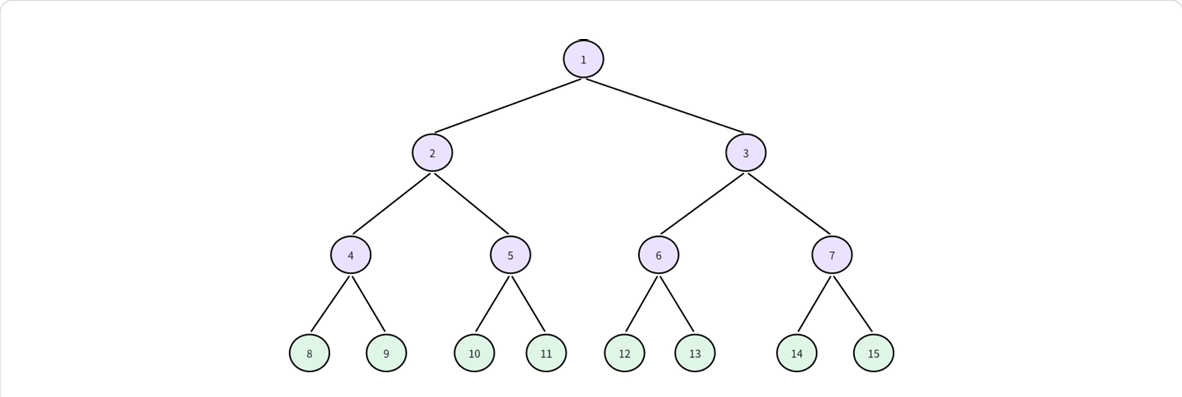
1.2.2 完全二叉树

对⼀棵树有n个结点的二叉树按层序编号，所有的结点的编号从1~n。如果这棵树所有结点和同样深度的满二叉树的编号为从1∼n的结点位置相同，这棵二叉树为完全二叉树，实际上就是在满二叉树的基础上，在最后⼀层的叶子结点上，从右往左依次删除若干个结点，剩下的就是⼀棵完全二叉树

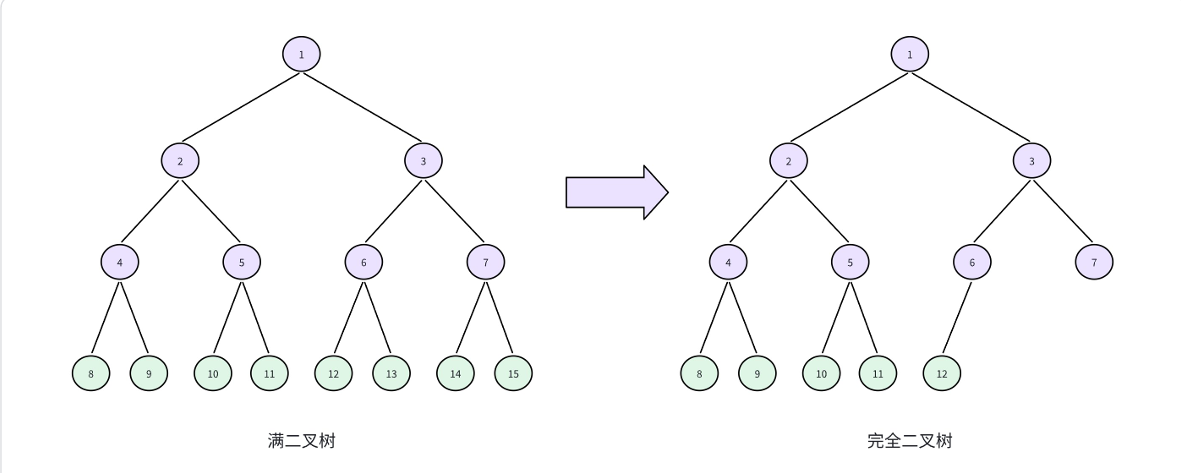
二、二叉树的存储

在之前已经学过树的存储，二叉树也是树，也是可以用vector数组 或者链式前向星 来存储。仅需在存储的过程中标记谁是左孩⼦，谁是右孩⼦即可。

• 比如用vector数组存储时，可以先尾插左孩子，再尾插右孩子；

• 用链式前向星存储时，可以先头插左孩子，再头插右孩子。只不过这样存储下来，遍历孩子的时候先遇到的是右孩⼦，这点需要注意。

2.1 顺序存储

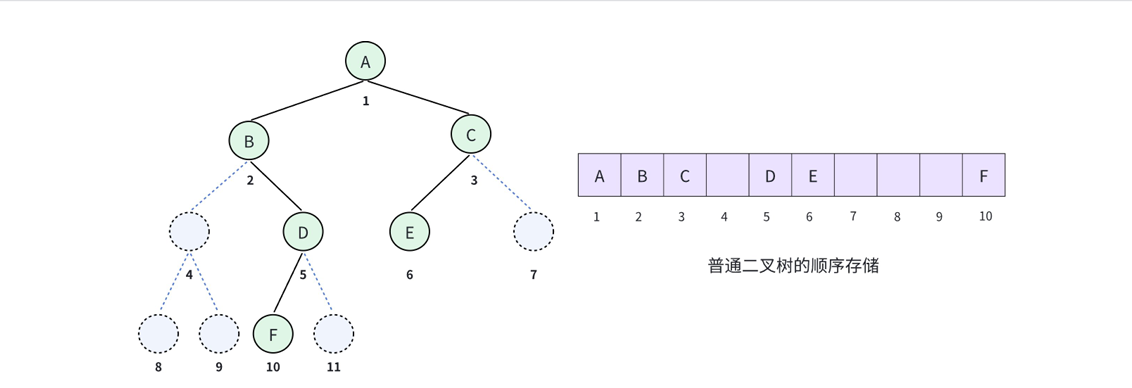
在完全二叉树以及满⼆叉树的性质那里，我们了解到：如果从根节点出发，按照层序遍历的顺序，由开始编号，那么父子之间的编号是可以计算出来的。那么在存储完全二叉树的时候，就按照编号，依次放在数组对应下标的位置上，然后通过计算找到左右孩子和父亲：设节点下标为i

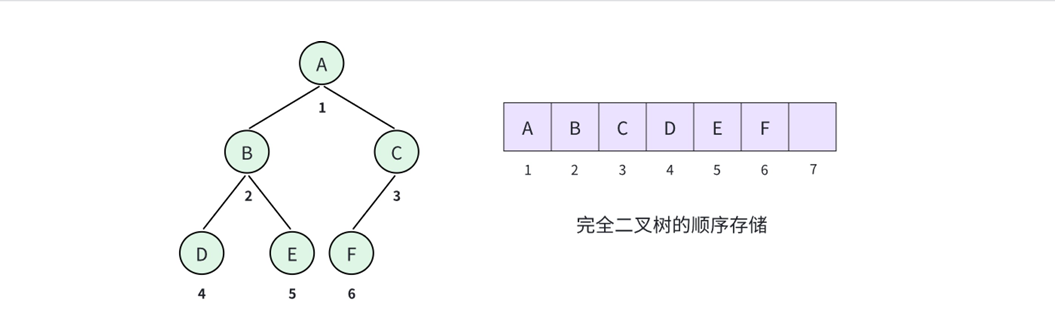
如果不是完全二叉树，也是可以用顺序存储。但是首先要先把这棵二叉树补成完全⼆叉树，然后再去编号。不然就无法通过计算找到左右孩子和父亲的编号

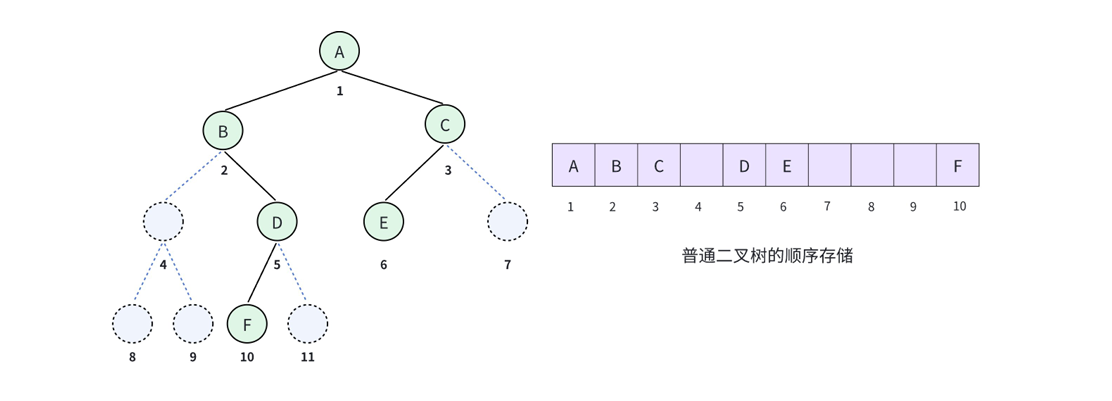
辨析：可以看到我们的二叉树其实只有6个节点，但是顺序存储却要分配10个空间，其中有4个空间都被浪费掉了。

如下图我们考虑⼀种极端的情况，⼀棵树右斜树，它只有4个节点，但是需要分配2^4 - 1个存储单元，这显然会对存储空间造成很大的浪费。所以，顺序存储结构⼀般只用于完全二叉树或满二叉树。

2.2 链式存储

可以创建两个数组l[N]，r[N] ，其中l[i] 表示结点号为i的结点的左孩⼦编号，r[i] 表示结点号为i的结点的右孩子编号

c 复制代码

#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int n;
int l[N], r[N];

int main()
{
   cin >> n;
   for(int i = 1; i <= n; i++)
   {
      // 存下 i 号结点的左右孩子
      cin >> l[i] >> r[i];
   }
   return 0;
}

三、二叉树的遍历

3.1 深度优先遍历

不同于常规树的深度优先遍历，二叉树因其独特的性质可以划分成三种深度优先遍历：先序遍历，中序遍历，和后序遍历。其中，三种遍历方式的不同在于处理根节点的时机。

对于⼀棵二叉树而言，整体可以划分成三部分：根节点+左子树+右子树：

• 先序遍历的顺序为：根+左+右；

• 中序遍历的顺序为：左+根+右；

• 后序遍历的顺序为：左+右+根。

3.1.1 先序遍历

c 复制代码

//先序遍历
void dfs1(int u)
{
	if (u == 0)   //递归出口
		return;
	cout << u << " "; //根
	dfs1(l[u]); //左
	dfs1(r[u]); //右
}

测试：

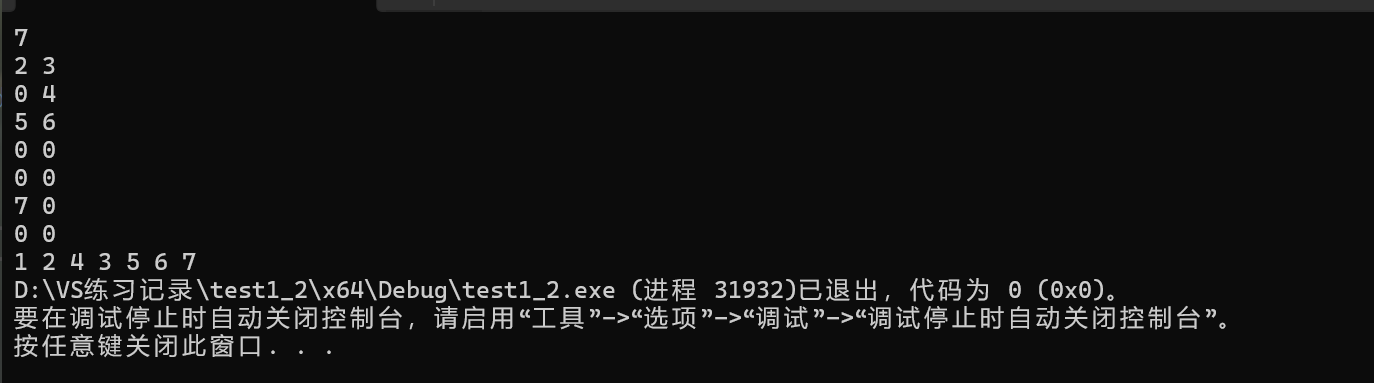
3.1.2 中序遍历

c 复制代码

//中序遍历
void dfs2(int u)
{
	if (u == 0)   //递归出口
		return;
	dfs2(l[u]); //左
	cout << u << " "; //根
	dfs2(r[u]); //右
}

测试：

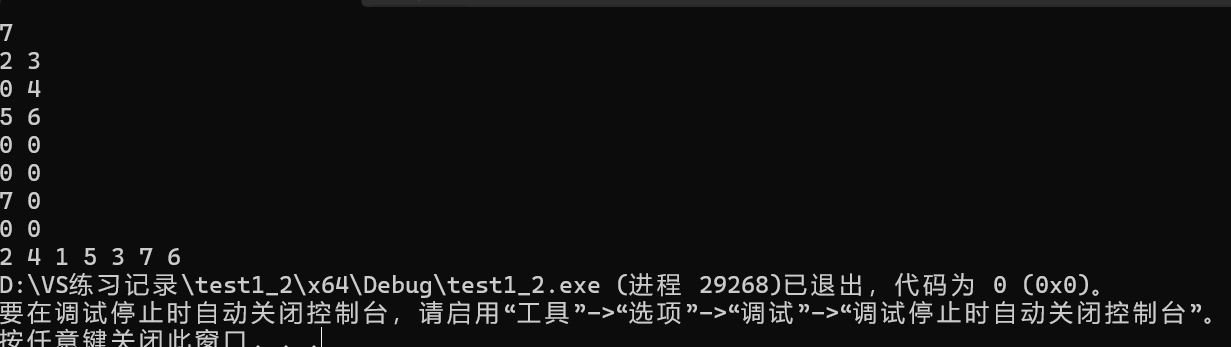
3.1.3 后序遍历

c 复制代码

//后序遍历
void dfs2(int u)
{
	if (u == 0)   //递归出口
		return;
	dfs2(l[u]); //左
	dfs2(r[u]); //右
	cout << u << " "; //根
}

测试：

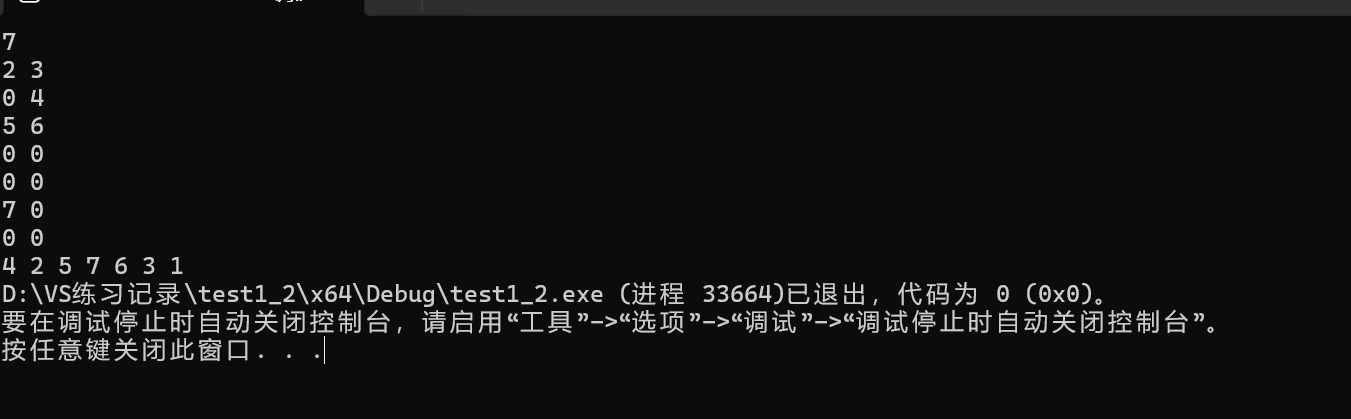
3.1.4 所有测试代码

c 复制代码

#include <iostream>
using namespace  std;
const int N = 1e5 + 10;
int l[N], r[N];

//先序遍历
void dfs1(int u)
{
	if (u == 0)   //递归出口
		return;
	cout << u << " "; //根
	dfs1(l[u]); //左
	dfs1(r[u]); //右

}

//中序遍历
void dfs2(int u)
{
	if (u == 0)   //递归出口
		return;
	dfs2(l[u]); //左
	cout << u << " "; //根
	dfs2(r[u]); //右
}

//后序遍历
void dfs3(int u)
{
	if (u == 0)   //递归出口
		return;
	dfs3(l[u]); //左
	dfs3(r[u]); //右
	cout << u << " "; //根
}

int main()
{
	int n;
	cin >> n;

	for (int i = 1; i <= n; i++)
	{
		cin >> l[i] >> r[i];
	}

	//dfs1(1); //先序遍历

	//dfs2(1); //中序遍历

	dfs3(1); //后序遍历

	return 0;
}

3.2 宽度优先遍历

这个就和常规的树的遍历方式⼀样，直接用队列帮助层序遍历即可。

c 复制代码

#include <iostream>
#include <queue>
using namespace std;
const int N = 1e5 + 10;
int l[N], r[N];

void bfs()
{
	queue<int> q;
	q.push(1);

	while (q.size())
	{
		int u = q.front();
		q.pop();
		cout << u << " ";

		// 左右孩⼦⼊队
		if (l[u]) 
			q.push(l[u]);
		if (r[u])
			q.push(r[u]);
	}
}
int main()
{
	int n;
	cin >> n;

	for (int i = 1; i <= n; i++)
		cin >> l[i] >> r[i];

	bfs();
	return 0;
}

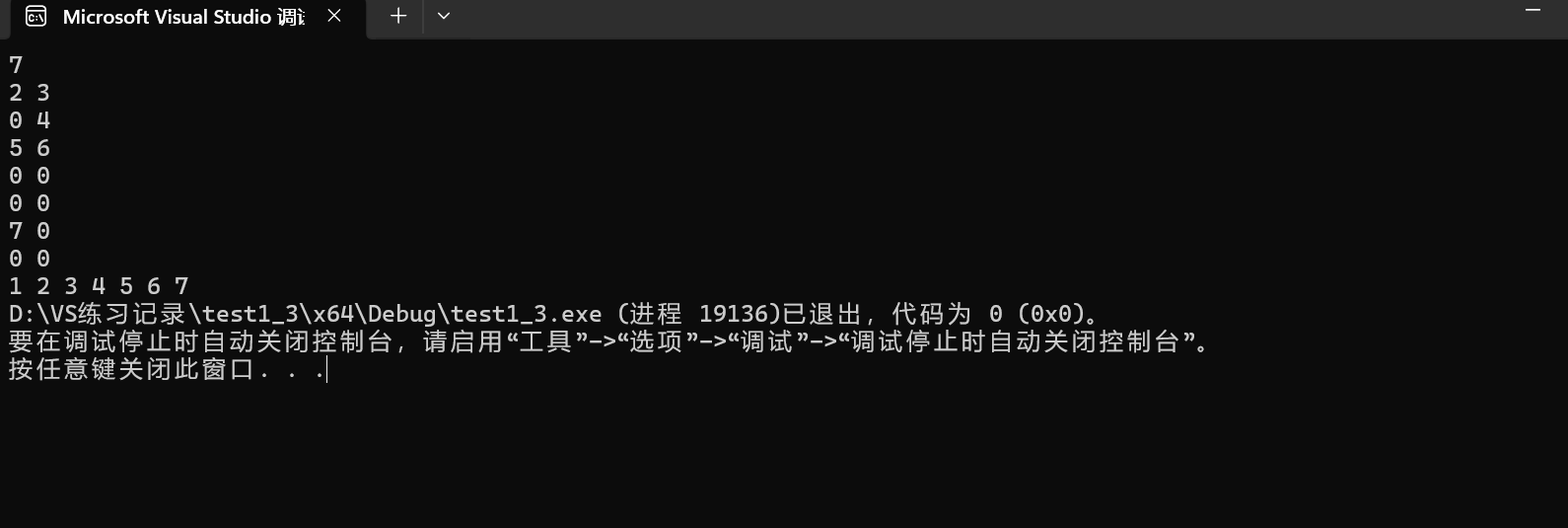
运行结果：

总结与每日励志

✨本文系统讲解了二叉树的基本概念、存储方式和遍历方法。首先介绍了二叉树的定义及其两种特殊形式（满二叉树和完全二叉树），然后详细阐述了顺序存储和链式存储两种方式的特点与适用场景。在遍历部分，重点讲解了深度优先遍历（先序、中序、后序）和宽度优先遍历的实现方法，并提供了完整的C++代码示例。文章最后以励志语句作结，鼓励读者坚持学习算法。全文结构清晰，内容实用，适合算法初学者快速掌握二叉树相关知识要点