递归遍历(前序)
1
/ \
2 3
遍历过程:
1. traversal(节点1, result)
│ result.push_back(1) → [1]
├─ traversal(节点2, result)
│ │ result.push_back(2) → [1,2]
│ ├─ traversal(左空, result) → 返回
│ └─ traversal(右空, result) → 返回
└─ traversal(节点3, result)
│ result.push_back(3) → [1,2,3]
├─ traversal(左空, result) → 返回
└─ traversal(右空, result) → 返回
最终结果:result = [1,2,3]
cpp
vec.push_back(cur->val); // 收集节点值
// vec 作为结果收集器,存储前序遍历的所有节点值。vector<int>& vec 的用途:
-
结果聚合器:收集递归遍历的所有结果
-
共享容器:所有递归层操作同一个容器
-
效率保证:避免拷贝,O(1)传递成本
-
数据一致性:确保所有修改都作用于最终结果
-
内存友好:不产生额外内存分配
本质 :这是一个输出参数(output parameter),通过引用传递让函数能够修改调用者提供的数据容器,是多层递归中传递和累积结果的常用模式。
cpp
class Solution {
public:
// 前序遍历递归函数
// cur: 当前遍历的节点指针
// vec: 存储遍历结果的引用(避免拷贝)
void traversal(TreeNode* cur, vector<int>& vec) {
// 递归终止条件:当前节点为空
if (cur == NULL) return;
// 1. 处理当前节点(中) - 前序遍历先访问根节点
vec.push_back(cur->val);
// 2. 递归遍历左子树(左)
traversal(cur->left, vec);
// 3. 递归遍历右子树(右)
traversal(cur->right, vec);
}
// 前序遍历入口函数
vector<int> preorderTraversal(TreeNode* root) {
// 创建结果容器
vector<int> result;
// 从根节点开始递归遍历
traversal(root, result);
// 返回遍历结果
return result;
}
};前序遍历(迭代法)
前序遍历是中左右,每次先处理的是中间节点,那么先将根节点放入栈中,然后将右孩子加入栈,再加入左孩子。
为什么要先加入 右孩子,再加入左孩子呢? 因为这样出栈的时候才是中左右的顺序。
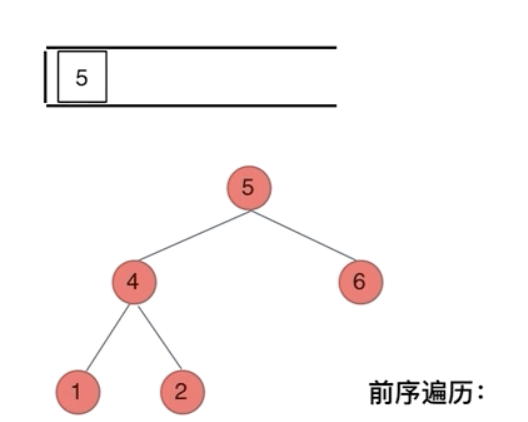
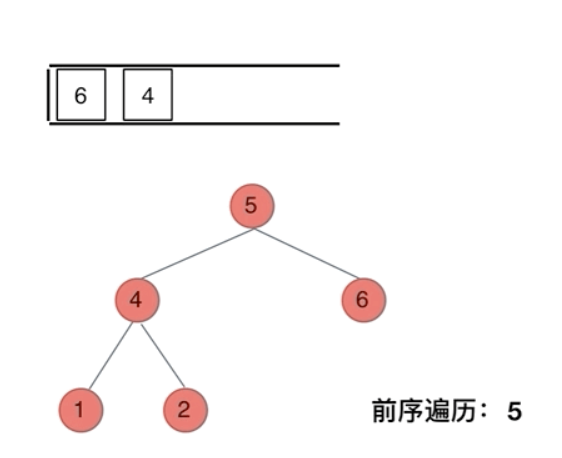
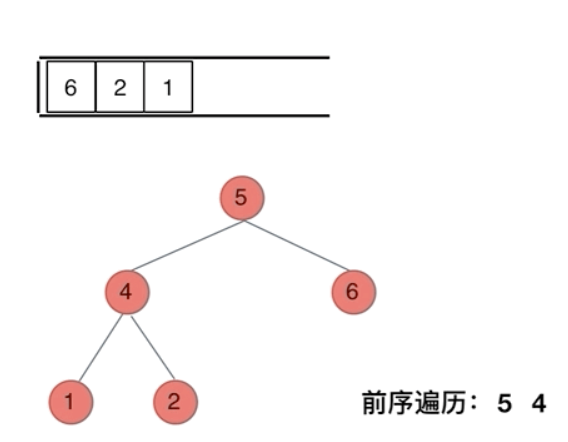
cpp
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
// 定义一个栈,用于存储待访问的节点
stack<TreeNode*> st;
// 存储前序遍历结果的数组
vector<int> result;
// 如果根节点为空,直接返回空结果
if (root == NULL) return result;
// 将根节点压入栈中(初始化)
st.push(root);
// 循环直到栈为空(所有节点都处理完毕)
while (!st.empty()) {
// 取出栈顶节点(当前要访问的节点)
TreeNode* node = st.top(); // 步骤1:访问当前节点(中)
// 弹出已取出的节点
st.pop();
// 将当前节点的值加入结果数组(执行访问操作)
result.push_back(node->val);
// 先压入右子节点(如果存在)
// 因为栈是LIFO(后进先出),为了保证访问顺序是"中左右",
// 需要先压入右子节点,这样左子节点会先被弹出访问
if (node->right) st.push(node->right); // 步骤3:右子节点入栈(空节点不入栈)
// 再压入左子节点(如果存在)
if (node->left) st.push(node->left); // 步骤2:左子节点入栈(空节点不入栈)
}
// 返回前序遍历结果
return result;
}
};