
这篇文章的灵感来自学习3D视觉算法知识点后课外的思考和自由探索,目前经过不完全的算法实验验证,成果差强人意,经过分析是数据采集的问题而非算法的设计问题。我将采取大白话+行云流水的方式分享,免去一些格式化的目录和结构,也免去较为基础的细节,从而确保这次要分享的内容主线清晰、篇幅合理。
本期算法难度稍大,需要一些矩阵计算和数字图像处理的前置知识。读者如若觉得理解存在困难,可先阅读笔者的"数字信号处理"专栏和"深度学习与终身学习"专栏的基础文章或学习基础知识。完整代码可以直接在个人空间下载,如果热销可能需要支付一定积分。本文将更侧重于理论和自然语言阐释,在伪代码和代码层面不过多阐述,以最小力实现最大功效。
首先,明确算法的目标。算法的目标是通过一台RGBD深度相机对一个场景中的摆件或者物体进行360°角的环绕拍照,得到4张-12张照片(或者更多),并还原出其数字化的3D模型。如果有用过腾讯混元3D大模型的朋友就知道,它支持文生3D和2D图生3D,包括现在拓竹等3D打印品牌也有提供手机拍摄绕周视频生成OBJ模型的功能,但限于手机缺乏深度信息,还原出来的模型效果存在一定缺陷,在细粒度方面也有较大提升空间。
这是一个较复杂的工程,涉及HSV色彩滤波、深度滤波的2D视觉算法(DIP-数字图像处理);点云计算(从RGBD到点云,点云体素下采样、点云随机下采样、点云拼接)、特征角点提取、含有尺度(大小)和方向信息的关键点匹配、最小二乘法/质心对齐法、ICP背景匹配算法等3D视觉算法。
本文使用奥比中光Gemini深度相机,以橘子作为待扫描物体,弊端是橘子的各个侧面差异较小,不容易检验算法的准确性和鲁棒性,但选择橘子的主要原因是------我喜欢吃水果,尤其喜欢吃橘子!!!
这个工程设计7个部分,其中第7部分受到实验硬件资源的影响,未进行验证,是可行的优化方向,第1部分和我写的"照片处理软件"这篇文章的思路大同小异,读者可先阅读此篇文章作为参考。
目录
[3.1 特征张量计算](#3.1 特征张量计算)
[3.2 区域匹配](#3.2 区域匹配)
[四、SFM 8点法估算旋转矩阵和平移方向向量(模长1)](#四、SFM 8点法估算旋转矩阵和平移方向向量(模长1))
五、(仅)含背景的点云集群固定点数下采样、最小二乘法估计平移尺度
一、点云和彩色图数据准备
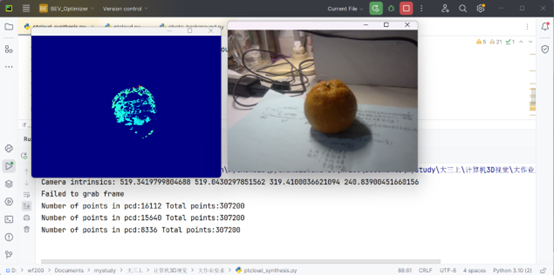
第一部分是本工程的头部,对于每个视角需要准备两张点云的ply文件和一张RGB图像,像Gemini深度相机的RGBD图像分辨率均为960x540。
第一个点云提取的是前景我们需要扫描还原的物体,第二个点云对应的是这个物体所处的远景信息,注意对于一般物体建议把前景物体滤除,也就是对应的掩码索引算子直接取反。但两者都需要滤除无效的深度点。
具体的方式也比较直观------只需要采样-计算-滤除三步。
采样:预先用同一个(深度)相机拍摄物体的表面纹理(色彩)信息,注意只适用于色彩均匀的局部区域;所以如果物体从不同角度看色彩差异很大,本算法暂不支持处理,需要读者自行加入支持【逐视角逐色彩样本】的色彩滤波算法(设计成列表读取格式,难度不大)。
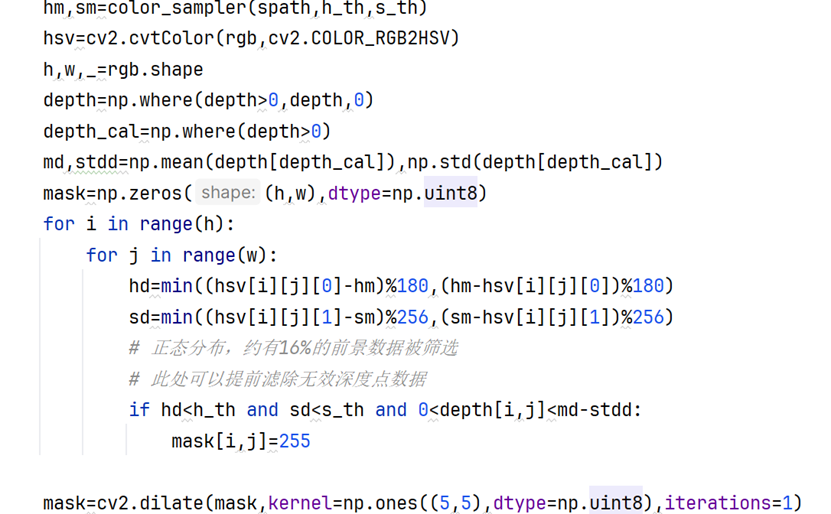
计算:把RGB图转到HSV的色调-饱和度-亮度空间,计算H色调和S饱和度的均值和标准差(衡量离散程度),如果样本的标准差超过阈值,则判定为无效样本,需要重新取样;同理,在计算实际的RGB转HSV图片时,把合格样本计算的H和S均值作为基线,如果图片中像素点的H和S的偏离程度没有超过阈值(可以另设一组也可以和采样图片区域共用一组,本实验设定H阈值5,S阈值25,H范围0-179,S范围0-254),则标记为目标像素点。
但是敏锐的读者很快注意到,这本质充其量就是一个颜色滤波算法而已。如果背景信息含有相近的颜色,算法的准确性和鲁棒性直接大幅下降,因为目标像素点和物体像素点完全是不同的概念,所以本算法为确保鲁棒性,还加入了深度滤波算法,结合待扫描物体的前景位置信息,把深度超过一定阈值的目标像素点禁用。
这样通过颜色滤波-深度滤波,得到的目标像素点集合和物体像素点集合就更相近了,在此基础上引入膨胀算法增强目标像素点集合的空间连续性,迭代1次,kernel核是5x5的全1矩阵。
而对于第二个点云ply,可以直接使用深度相机拍到的前后景RGBD计算得到,也可以加入一个滤除前景物体的操作以确保本文第7部分的算法有效(限于资源问题,暂未验证)。
二、Harris角点提取
使用Harris角点检测器,此处把0-255的像素值在计算的时候进行了归一化处理,确保Harris像素点特征值的范围在经典范围之内,静态阈值体系可以共通,但本文使用的是动态阈值,根据最大角点特征值乘以阈值比例系数计算动态阈值。
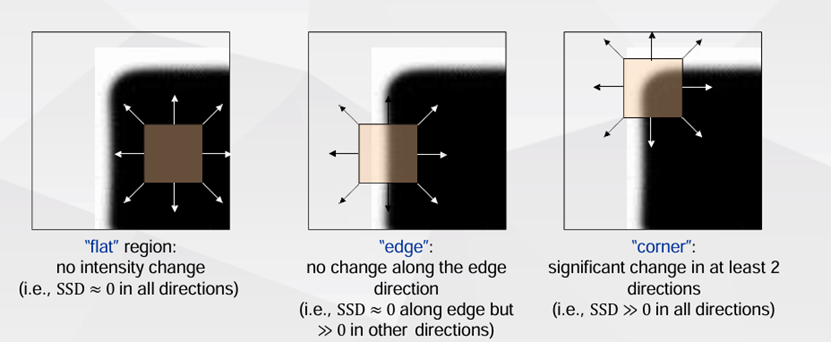
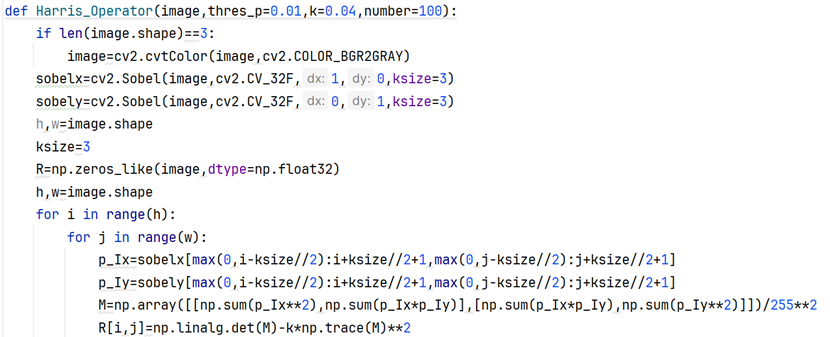
其实Harris操作算子仅仅是在描述像素强度沿X、Y方向的变化。先使用Sobel-x、Sobel-y算子(121型),然后构造2x2特征矩阵,最后通过矩阵的行列式和迹计算R[i,j]值。矩阵的迹是对角分解后,对角矩阵特征值之和,行列式是对角矩阵特征值之积。
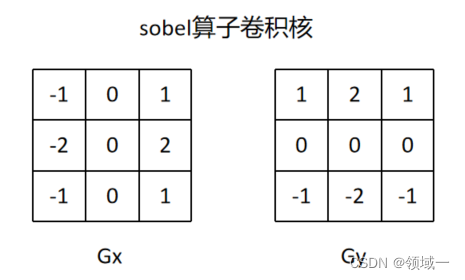
注意最终计算式中,k是手调参数,经验值是0.04左右,根据高中数学基本不等式的知识,这时R[i,j]的上限是0.84*a1*a2(a1,a2是对角矩阵特征值),显然特征值同正或同负,因为M特征矩阵的行列式非负(一般是正数)。都当做正数来看,当是边缘上的点(非角点)时,R值为较小的负数(绝对值较大);当是亮度平稳变化的内部像素点时,R值为接近0的值;只有在角点上,才是一个较大的正数。得到R矩阵之后进行3x3高斯模糊和一个闭运算(先膨胀后腐蚀)。

这时再利用第二部分前面提到的动态阈值得到二值图像掩膜,thres_p设为0.01,number是负责控制最大角点个数的,防止只有阈值设定时造成的鲁邦失衡,本实验设定为1000,k值0.04。
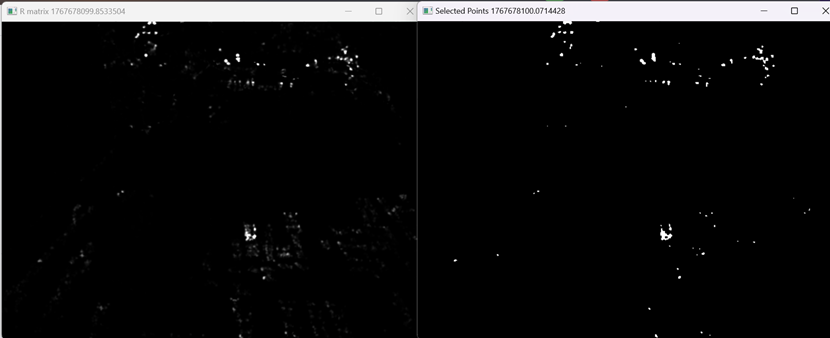
从这一部分的实验结果来看,1000个角点的图片和只经过高斯滤波的R矩阵(还未闭运算和二值化)有部分角点的滤除。
三、特征张量计算和区域匹配
3.1 特征张量计算
因为本实验设置的是最多1000个角点,根据实验情况来看,0.01的动态全局比例可以产生多于10000个合格角点,所以使用1000进行数量限制,取前1000个特征值最大的像素点作为合格角点(如果是并列,按照从左到右、从上到下的顺序选择)。
对于得到的1000个角点,需要计算特征矩阵以进行特征点的匹配,注意不是说这两张图片的1000个点一定是完全一一对应,而且我们在第4部分只需要8个特征点对,因此在双for循环匹配完成后,我们根据ssd的指标取匹配度最高的8个单射作为匹配区域。
在计算特征张量的时候,默认尺寸8x8x3(HWC),两张图的每个特征点都有这样一个192个元素的张量。但是这个张量是怎么计算得到的呢?

很显然,每个特征点代表着灰度图片亮度变化剧烈的地方,那这里自然包括变化剧烈是朝着哪个方向去的、以及这里的轮廓信息的隐藏空间尺度(patch大小)信息。课内讲授的时候并未具体说明用什么指标选择最佳尺度,我查阅了课外资料,最终选择了灰度图空间下的patch的标准差(numpy.std)作为指标,实验结果证明是合适的指标。
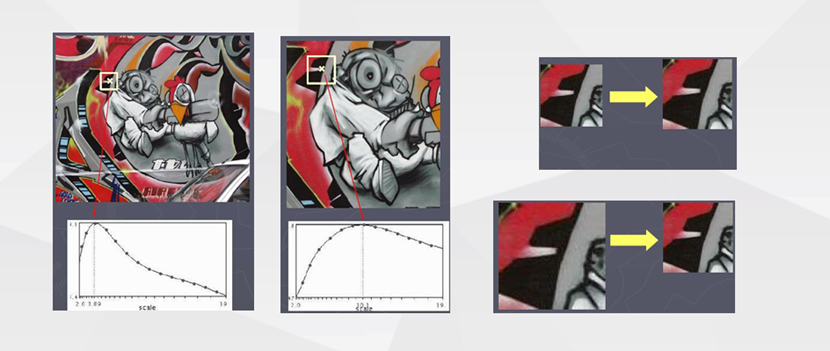
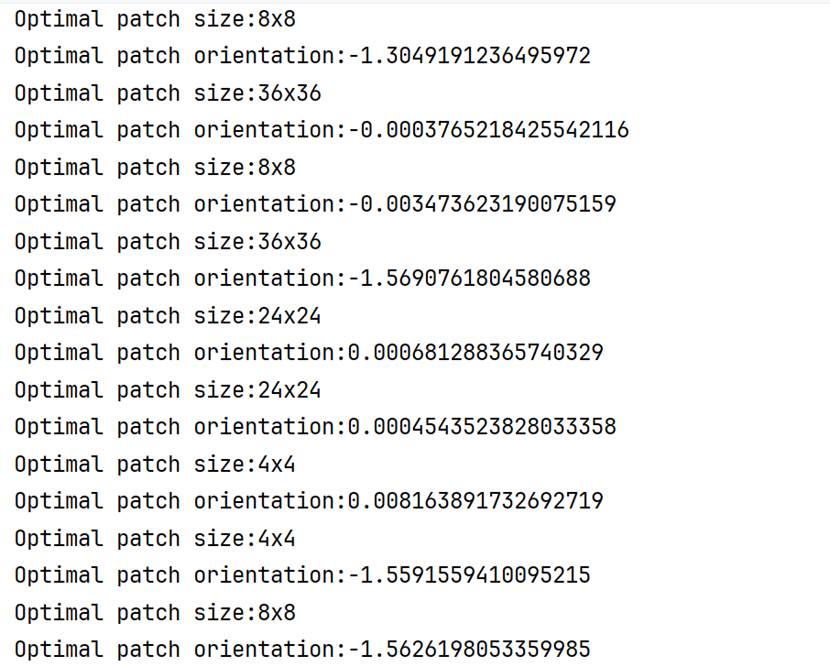
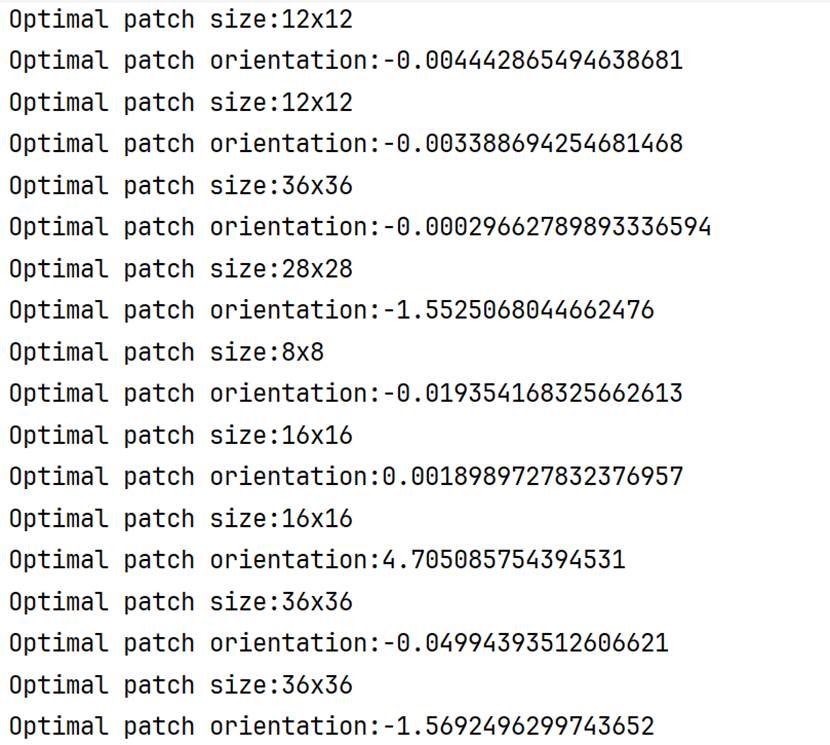
在这里首先在候选尺寸列表(本算法设定4到38,步长2)里面,对于每一个尺寸应用Sobel-X和Sobel-Y算子,然后同样构建一个类似Harris算子-M矩阵的点相特征矩阵;然后进行特征对角分解,选取主导的特征向量(特征值较大的那个)反正切函数计算得到朝向角度。这样,1000个特征点每个点都有(38-4)/2+1=18个角度和18个std标准差。根据标准差选择最佳尺度和对应角度即可。
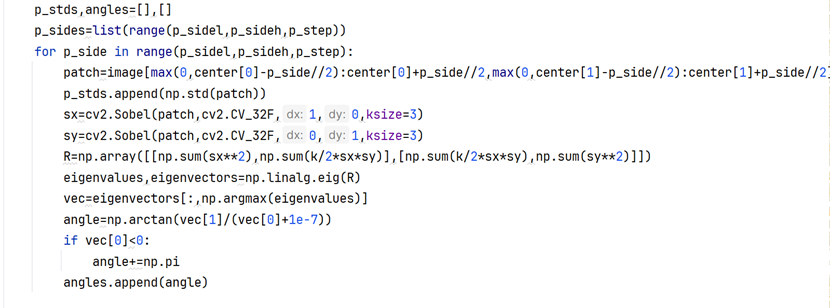
实验过程截图
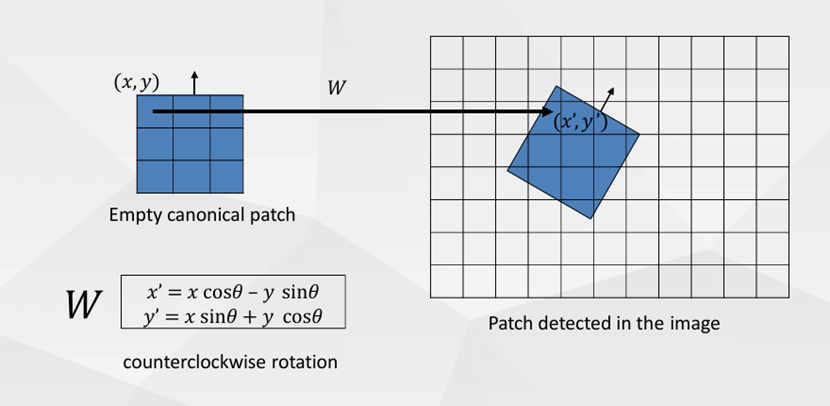
接下来只需要计算特征张量,注意前述的最佳尺寸和角度是在灰度空间中计算,而特征张量是HWC的彩色空间张量。先根据确定的最佳尺寸切片出空间尺寸未旋转的mxmx3的patch,使用双线性插值变为8x8x3;使用线性代数的知识,构造旋转矩阵,从全0张量根据最佳角度旋转到和切片patch"朝向一致",但注意旋转的时候需要先做一个坐标中心和张量空间中心对齐的前后平移处理(存在负数坐标,确保旋转的物理意义);使用双线性插值,注意只对内切圆内部和内切圆上的像素点计算数值,避免旋转超出空间边界数据无效的情况。

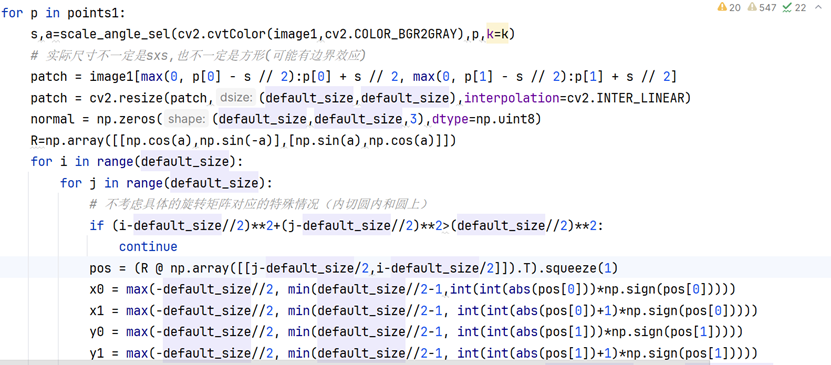

注意:和课内做法完全不同,课内做法用到LoG算子搜索最佳尺度而非std标准差。

3.2 区域匹配

进行1000x1000的双循环遍历,遍历过程中不做单射的限制,遍历完成后得到1000个匹配结果,并根据ssd(sum of squared distance,平方和距离)排序筛选出前8个单射的结果,注意这里不具备交换律,也就是说第一张和第二张图的patches内外循环交换,得到的前8个结果很可能就不同了。这也是后续算法精进的一个点。

四、SFM 8点法估算旋转矩阵和平移方向向量(模长1)
每个深度相机的内参不同,可以通过opencv内置API获取,此处代码里面直接手动根据API结果录入。


SFM是估计拍摄两张2D图片的同一相机(不一定是深度相机)的运动姿态变换的算法。只能较精确地估计旋转矩阵和平移方向向量(单位向量),如果获得了尺度信息,就可以获得完整的变换矩阵,从而直接运用于3D物体(或场景)重建了。
首先计算从2D像素整数坐标到3D空间(此处单位毫米),构建8x9的矩阵,注意如果是x2y2主导行,就是从第二张图变换到第一张图的矩阵。如果是反过来,就需要转置矩阵。
目前关于对极约束和本质矩阵计算的原理笔者还不了解。但代码是可以写出来的。8x9的非方阵矩阵不能够使用特征对角分解,所以使用SVD进行矩阵分解。
分解之后注意确保中间的矩阵的前两个特征值相等,第三个特征值为0(意思应该是缺少尺度信息,3维世界投影到2维相机画幅,只有两个维度有效),所以做出算术平均处理。

有趣的是,这里的t确实百分百含量是一个单位向量(numpy.linalg.norm验证为1)。但实际过程中,在3D视觉算法中,变换矩阵是一个4x4的矩阵,在点云拼接部分只需要把R和t拼接起来即可。
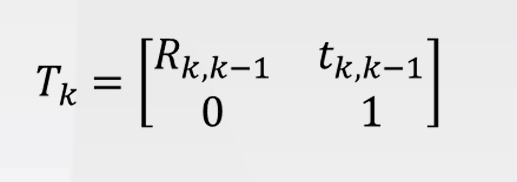
五、(仅)含背景的点云集群固定点数下采样、最小二乘法估计平移尺度
从结果来看,Harris算子、动态阈值与最大角点数设定、角度尺度计算、方向对齐和双线性插值设计、区域匹配、SFM 8点法估计变换矩阵得到的R(旋转矩阵)已经比较精准了,主要问题出在t的尺度上。那么这个时候第二个点云(远景信息)的作用就是调整平移向量的尺度,因为SFM估计的t是单位向量,对应长度1毫米,显然不符合实际情况。
本实验的远景信息点云并没有去除前景物体,同时前景物体(第一个点云)也没有进行深度滤波,所以用MeshLab查看实际拼接效果(见第6部分成果展示)的时候,会发现除了橘子的"一瓣表面"之外,还有很多背景的杂质点群。所以使用的方法也仅仅限于第6部分的最小二乘法和ICP精配准,未使用第7部分的质心法,因为质心法对于前景物体点云的提纯度有很高要求。
因为最小二乘法要求两个远景点云集群点数一致,所以需要先进行固定点数的下采样,open3d库没有直接提供FPS(Furthest Point Sampling,不是帧率或者战术射击游戏)最远点采样算法,该算法可以在保持点云基本的空间分布的前提下实现固定点数采样。
本算法在这一部分通过体素下采样+随机点数下采样组合的方式实现,不存在采样后点数少于目标点数,通过线性插值补足的情况。体素下采样不能精确控制点数但可以维持空间结构,随机采样不能确保结构稳定(特别是采样点数远小于实际总点数时)但可以精确控制点数,所以先通过二分法选择合适的提速大小voxel_size,得到略高于目标点数的实际点数,然后使用随机下采样获得最终点云。本实验目标点数target_num=10000,偏差比例(只多不少)bias_p=1。最小最大体素体积不可外部更改,分别为1e-4毫米和100毫米。体素下采样二分法迭代过程如下图所示,设置最大迭代轮数避免出现由于点云分布的空间属性问题导致低偏差比例设定下无法满足终止条件的情形:
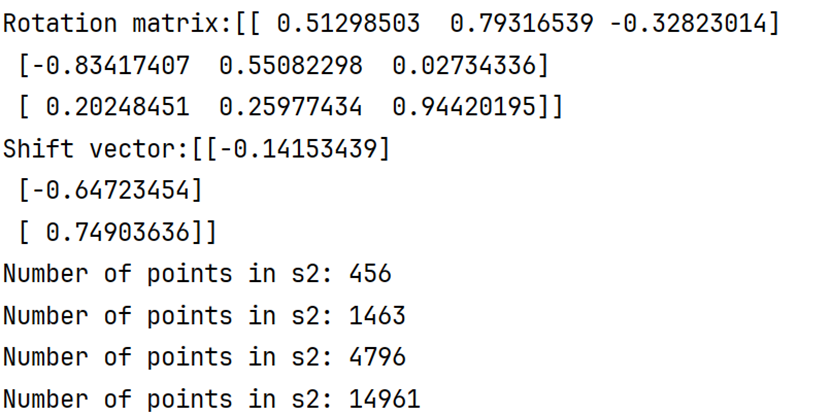
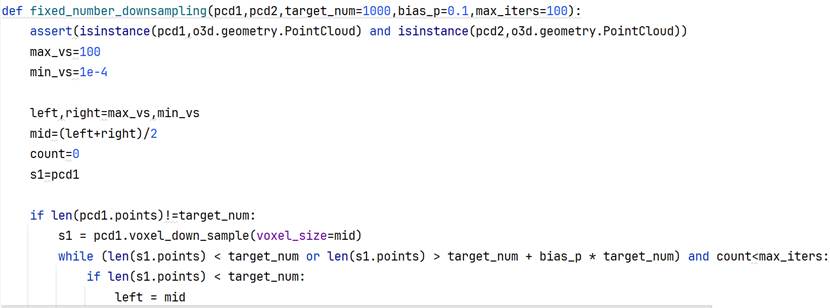
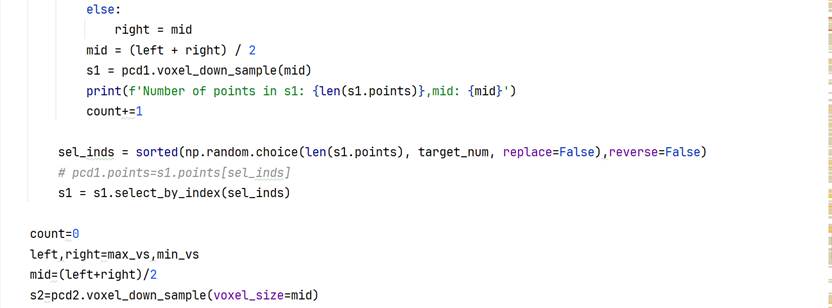
但由于最小二乘法不仅需要点数一致,还严格依赖两组点云的顺序或者对应关系。本算法在处理顺序对应关系上的策略还有较大的优化空间,目前通过排序(从小到大)的方式对应,但实际上受到物理场景和点云集群分布的影响,固定点数下采样之后得到的点云序列基本上没有什么对应关系,同理在下采样之前的点云因为深度信息的缺失,960x540=518400约52万个点实际只有27万左右的有效3维点,在一开始两组点云的点就不是一一对应。
即使没有任何数据缺失,像素点的空间对应和实际场景的"语义对应"也是完全不同的概念,比如一个橘子在这个点云中的顺序索引集中在位置X周围,在第二个点云中可能由于相机视角和拍摄物理场景的改变,导致橘子的拍摄位置发生变化(比如从画幅居中到画幅右侧),从而围绕的中心顺序变成了X+Y,发生了后移。所以实际上最小二乘法估计的尺度十分不准,需要进行后处理。
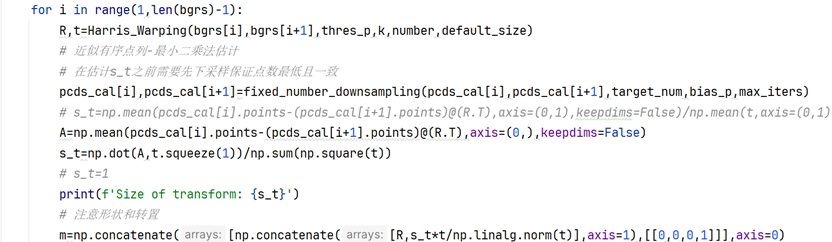
最小二乘法尺度公式的推导,读者可以参考文末的"参考资料"部分其他博主的推导,或者直接参考统计学里线性回归斜率的求解公式推导,本质一致。
六、后处理:ICP精配准、点云拼接与导出
这一部分需要注意四个点:
- 矩阵的转置情况;
- icp精配准的max_correspondence_distance设定;
- pcds_cal[i+1]调用transform方法前的预先备份;
- 相邻变换矩阵和全局变换矩阵的关系(全局变换矩阵是相邻变换矩阵按照变换序列顺序依次进行矩阵右乘得到的)。
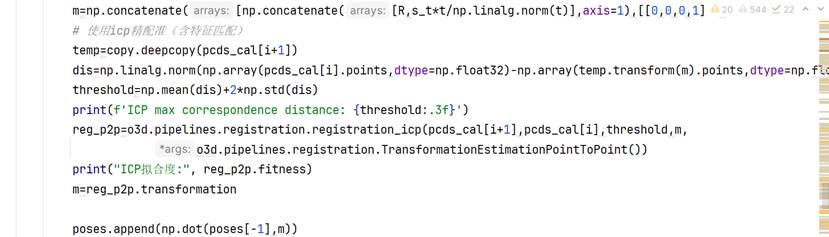
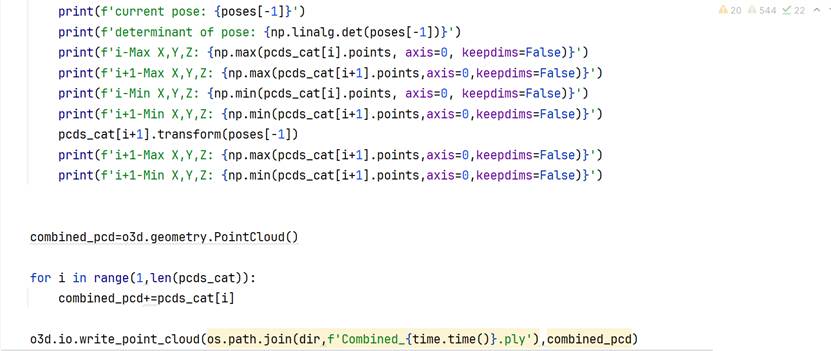
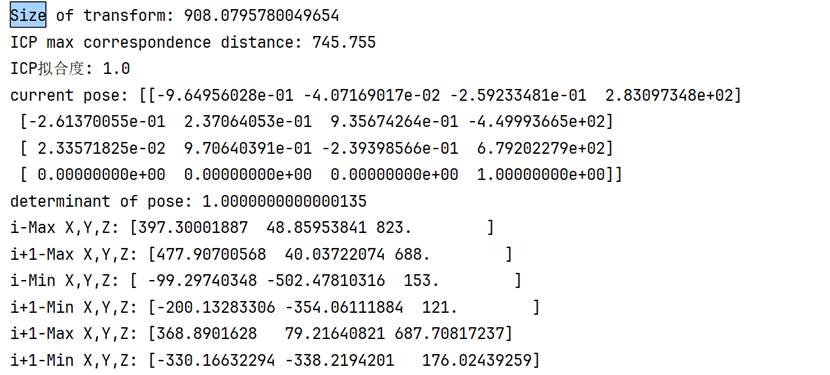
可以通过变换矩阵的行列式、xyz的极值、变换后z的最小值的非负性检验变换的基本合理性。
需要注意的是,如果行列式值为负,就需要重新调整旋转矩阵。下面四张图是行列式为-1的情况,明显出现橘子倒置的情况,旋转矩阵出现问题。其中第三张是没有使用ICP精配准后处理的结果,第四张时使用了后处理的结果。





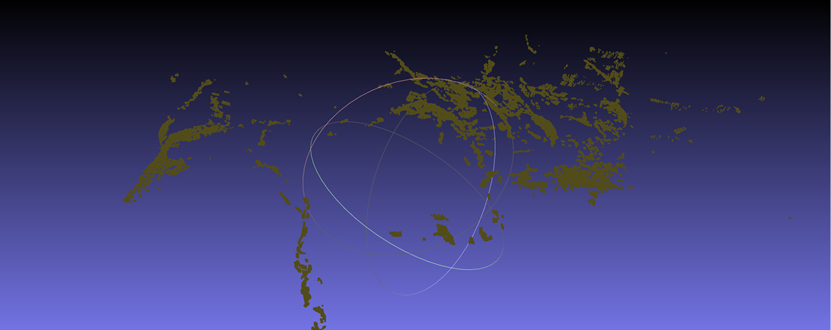

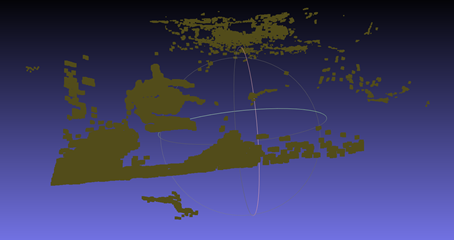

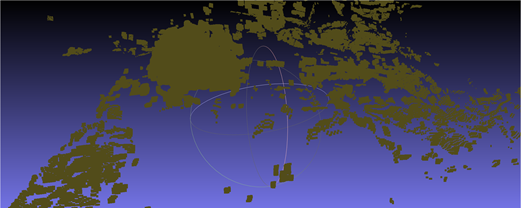


可以看到,在行列式校对为+1之后,三个视角的点云旋转关系正常。但效果不好的原因也很明显,360°的视角需要8-12张照片才能有较好的效果,因为过少的照片信息意味着相邻两张照片远景信息的重合度更低,在匹配特征点的时候容易出现"强扭的瓜不甜"的现象,造成特征点对受伪的情况。虽然实验中设置了1000组非单射匹配点对,选了匹配度最高(ssd最低)的前8个单射点对,然而对绝对值未做要求,实际上ssd数值已经较高。192个元素的特征向量,范围[0,255],设定的ssd阈值是100000,意味着只有平均每个元素绝对值差距小于等于22(左右)才是有效匹配特征点对,根据实测结果,6000-8000左右的ssd算是比较低的了,也就是平均每个元素的绝对值误差在5.5-6.3左右。
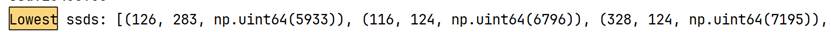
如果角度照片增加到8张(45°)、12张(30°)、16张(22.5°),前8个单射的ssd会更低。
说一个有意思的事情,我在实验验证的时候只拍了4张照片(前后左右),而且第一张正面照片和相关的两组点云丢失了。所以并不是算法本身的问题,而是数据采集的问题。
(行列式为-1)调整方式:在SFM八点法函数内部计算旋转矩阵时,W换成W.T转置矩阵。

七、使用质心法直接计算平移向量(暂未验证)
主要区别在于平移向量t的计算方式,使用质心法的前提是前景物体点云(第二个点云)的提纯度较高,只用到1-4部分计算得到的R旋转矩阵。

参考资料
1\] [基于Python的Structure from Motion(SfM)三维重建实战教程-CSDN博客](https://blog.csdn.net/weixin_35826166/article/details/141575214 "基于Python的Structure from Motion(SfM)三维重建实战教程-CSDN博客") \[2\] [【PCL】------ 点云配准ICP(Iterative Closest Point)算法_icp点云配准-CSDN博客](https://blog.csdn.net/sinat_52032317/article/details/130441840?spm=1001.2014.3001.5506 "【PCL】—— 点云配准ICP(Iterative Closest Point)算法_icp点云配准-CSDN博客")