P5490 【模板】扫描线 & 矩形面积并
题目描述
求 n n n 个四边平行于坐标轴的矩形的面积并。
输入格式
第一行一个正整数 n n n。
接下来 n n n 行每行四个非负整数 x 1 , y 1 , x 2 , y 2 x_1, y_1, x_2, y_2 x1,y1,x2,y2,表示一个矩形的四个端点坐标为 ( x 1 , y 1 ) , ( x 1 , y 2 ) , ( x 2 , y 2 ) , ( x 2 , y 1 ) (x_1, y_1),(x_1, y_2),(x_2, y_2),(x_2, y_1) (x1,y1),(x1,y2),(x2,y2),(x2,y1)。
输出格式
一行一个正整数,表示 n n n 个矩形的并集覆盖的总面积。
输入输出样例 #1
输入 #1
2
100 100 200 200
150 150 250 255输出 #1
18000说明/提示
对于 20 % 20\% 20% 的数据, 1 ≤ n ≤ 1000 1 \le n \le 1000 1≤n≤1000。
对于 100 % 100\% 100% 的数据, 1 ≤ n ≤ 10 5 1 \le n \le {10}^5 1≤n≤105, 0 ≤ x 1 < x 2 ≤ 10 9 0 \le x_1 < x_2 \le {10}^9 0≤x1<x2≤109, 0 ≤ y 1 < y 2 ≤ 10 9 0 \le y_1 < y_2 \le {10}^9 0≤y1<y2≤109。
Updated on 4.10 by Dengduck(口胡) & yummy(实现):增加了一组数据。
代码+注释
cpp
#include <bits/stdc++.h>// 万能头文件:包含所有算法/STL/输入输出需要的头文件
using namespace std;// 释放std命名空间,避免每次写std::
typedef long long int ll;// 数据类型重定义:把long long简写为ll,防止面积爆int
const int N=1e5+5;//题目中n最大是1e5个矩形
struct lines{//扫描线
int y,//该扫描线的纵坐标(矩形上下边),两个扫描的纵坐标差*扫描线有效宽度得该部分面积
l,r,//扫描线存储的矩形左右界点横坐标
state;//扫描线的类型:+1=入边(矩形的下边界,将该区间加入有效宽度),-1=出边(矩形的上边界,从有效宽度删除这个区间)
bool operator<(const lines &b)const{return y<b.y;}//&引用,避免拷贝,节省时间。const常量标识,避免修改
//扫描线以y轴从小到大排序,从下往上处理
}line[N<<1];//矩形有上下两边,所以这里*2
/*
线段树,用当前扫描线区间快速维护扫描线所在矩形集合横截面的有效宽度
*/
struct node{//线段树节点,矩形横截面
int l,r,
/*
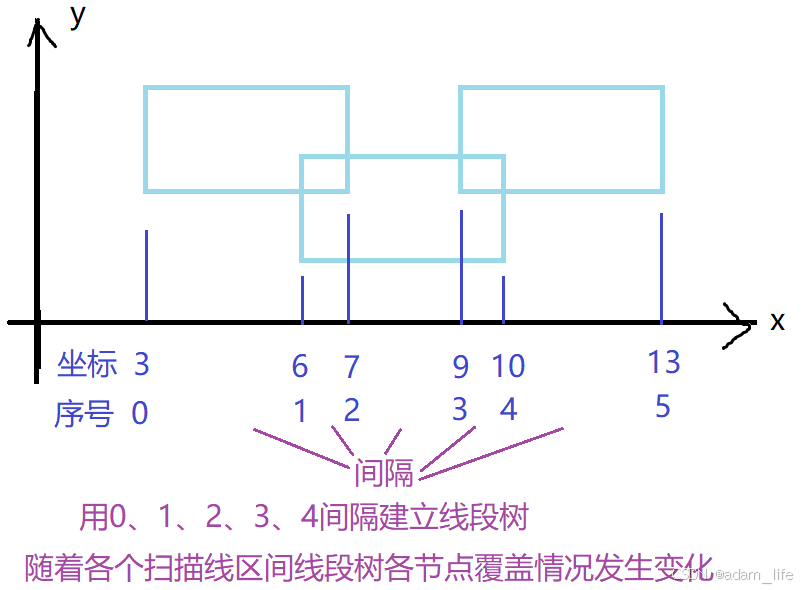
线段树各节点左右边界点的序号(各点是带右间隔的序号如0、1、2、3,这就有4个间隔,可能是1-3-5-8-12)
各矩形左右界点坐标 2 5 8 9
线段树原数列序号 0 1 2 3
0表示2到5间隔
1表示5到8间隔
2表示8到9间隔
*/
cnt_state;
/*
各扫描线覆盖状况,先有"矩形入边"后才有"矩形出边",所
以可以多次覆盖>0,最小只能=0。
*/
ll width;//扫描线有效长度。
}tree[N<<3];//线段树节点起码是原数列的4倍<<2,这里的原数列是单个序号表示的间隔数,这间隔最多是矩形数*2-1.
vector<int> v;//线段树原队列,存放各矩形(左右)界点坐标。开不了1e9的数组,用这容器完成离散化。
int n,id;
ll area;//所有矩形面积和
void build(int f,int l,int r){//构建线段树(对应原数列(各间隔序号))
tree[f]={l,r,0,0};//初始化节点的左右边界等属性
if(l==r)return;//叶子节点,不用再拆了。r不是矩形的右边界,是该区间最后一个间隔。
int m=l+((r-l)>>1);//区间中点
build(f<<1,l,m);//递归构建左半部分线段树,节点编号f*2
build(f<<1|1,m+1,r);//递归构建右半部分,f*2+1
}
int find(int x){//得到矩形左右界点x坐标在原数列里的下标
return lower_bound(v.begin(),v.end(),x)-v.begin();
//二分查找大于等于X的元素,返回该元素的迭代器(指针),同v.begin()的差就是该元素的下标
//x坐标(太大)转换成原数列里的下标,这就是离散化
}
void pushup(int f){// 更新线段树节点维护的「有效横向宽度」(扫描线核心:当前节点覆盖的有各矩形区域的宽度和)
int l=tree[f].l, r=tree[f].r; // 当前节点维护的离散化区间下标范围(l/r是区间下标,非坐标点下标)
if(tree[f].cnt_state>0) // 核心:当前区间被矩形完全覆盖(cnt_state>0表示有至少1个矩形覆盖)
tree[f].width = v[r+1] - v[l]; // 计算完整区间的真实宽度:离散化坐标v[r+1]-v[l](对应真实x轴区间长度)
//右界r指最右边的间隔,如0,1,2,3,4------l=1,r=3,指有1、2、3三个间隔,之间距离是v[r+1]-v[l]
// cnt_state==0时,分两种情况处理:
else if(l == r) // 情况1:cnt_state要么>0要么==0,现在==0。
tree[f].width = 0; // 叶子节点无覆盖时,有效宽度为0
else// 情况2:当前节点是非叶子节点(需合并左右子节点的有效宽度)
tree[f].width = tree[f<<1].width + tree[f<<1|1].width; // 左右子节点有效宽度之和 = 当前节点有效宽度
}
void update(int f,int s,int e,int state){// 扫描线核心:更新线段树中[s,e]区间的覆盖次数(state=1插入矩形/state=-1删除矩形)
int l=tree[f].l, r=tree[f].r; // 当前线段树节点维护的离散化区间下标
int m = l + ((r - l) >> 1); // 计算当前节点区间的中点
// 情况1:当前节点的区间被[s,e]完全包含(完全覆盖)
if(s <= l && r <= e){
tree[f].cnt_state += state; // 更新覆盖次数:+1(插入矩形)/-1(删除矩形)
pushup(f); // 立即更新当前节点的有效宽度(cnt_state变化后需重新计算width)
return; // 无需递归子节点(完全覆盖,子节点无需更新)
}
// 情况2:当前节点的区间与[s,e]部分重叠,递归处理子节点
if(s <= m) update(f<<1, s, e, state); // 左子树(f<<1)与[s,e]有交集,递归更新左子树
if(m < e) update(f<<1|1, s, e, state); // 右子树(f<<1|1)与[s,e]有交集,递归更新右子树
pushup(f); // 回溯更新:子节点更新完成后,重新计算当前节点的有效宽度
}
int main(){
//freopen("data.cpp","r",stdin);
cin>>n;
for(int i=0;i<n;i++){
int x_1,y_1,x_2,y_2;
cin>>x_1>>y_1>>x_2>>y_2;
line[id++]={y_1,x_1,x_2,1};//矩形上边入边,state=1
line[id++]={y_2,x_1,x_2,-1};//矩形的上边界 → 出边,state=-1
v.push_back(x_1);//各矩形左右边,用来构造线段树的原队列
v.push_back(x_2);
}
sort(line,line+id);// 按结构体的重载规则:按y坐标从小到大排序,保证从下到上扫描
// ===== 步骤2:对所有矩形左右边坐标做【离散化】处理 =====
sort(v.begin(),v.end());//把所有x坐标从小到大排序
v.erase(unique(v.begin(),v.end()),v.end());// 去重,unique把重复元素移到末尾,erase删除末尾重复元素
build(1,0,v.size()-2);//对所有间隔构建线段树。n个矩形最多又n*2-1个间隔。序号从0开始,所以最后一个序号是n*2-1-1
for(int i=0;i<id-1;i++){
int y=line[i].y,
l=line[i].l,
r=line[i].r,
state=line[i].state;
update(1,find(l),find(r)-1,state);//更新l到find(r)-1这些间隔的矩形覆盖情况
area+=tree[1].width*(line[i+1].y-y);//有效宽度*高度
}
cout<<area;
return 0;
}
小结
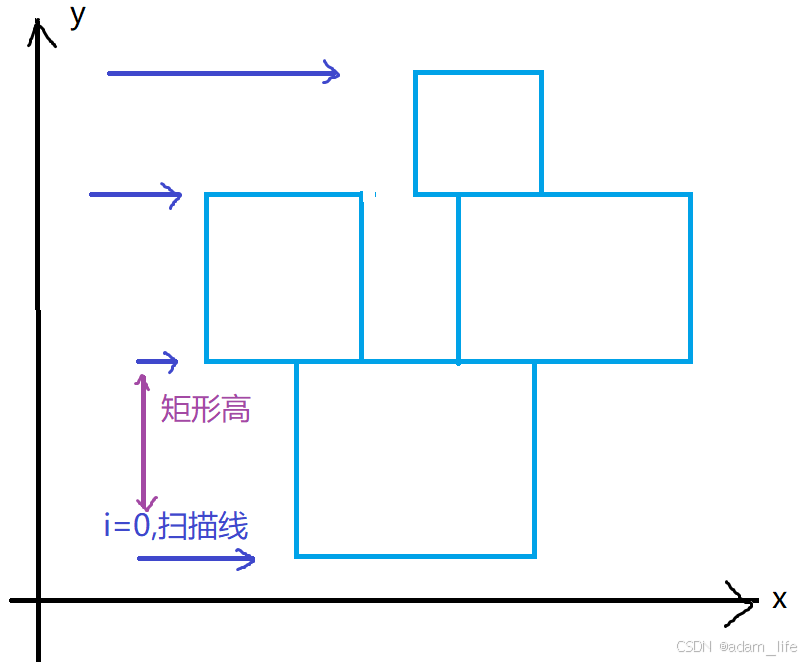
面积核心公式:有效宽度 × 相邻扫描线的高度差 = 单层矩形面积增量,累加所有增量得到总面积;
扫描线的核心作用:将 y 轴按矩形上下边界拆分,相邻两条扫描线的纵坐标差 = 计算面积的「高度」;
线段树的核心作用:随着扫描线从下到上遍历,高效维护当前 y 轴位置的「有效宽度」(被矩形覆盖的 x 轴总长);
线段树的叶子节点:对应 x 轴离散化后的「最小区间(相邻坐标点的间隔)」,而非单纯 "间隔";
线段树更新规则:每次用当前扫描线对应的矩形左右边界(离散化后下标),更新线段树的区间覆盖状态,进而计算有效宽度。