硅基计划4.0 算法动态规划高阶

文章目录

一、双数组DP
- [1. 最长公共子序列](#1. 最长公共子序列)
- [2. 不相交的线](#2. 不相交的线)
- [3. 不同的子序列](#3. 不同的子序列)
- [4. 通配符匹配](#4. 通配符匹配)
- [5. 正则表达式匹配](#5. 正则表达式匹配)
- [6. 交错字符串](#6. 交错字符串)
- [7. 两个字符串最小ASCII删除和](#7. 两个字符串最小ASCII删除和)
- [8. 最长重复子数组](#8. 最长重复子数组)
二、背包问题
- [I. 01背包问题](#I. 01背包问题)
- - [1. 模板题](#1. 模板题)
  - [2. 分割等和子集](#2. 分割等和子集)
  - [3. 目标和](#3. 目标和)
  - [4. 最后一块石头重量II](#4. 最后一块石头重量II)
- [II. 完全背包](#II. 完全背包)
- - [1. 模板题](#1. 模板题)
  - [2. 零钱兑换](#2. 零钱兑换)
  - [3. 零钱兑换II](#3. 零钱兑换II)
  - [4. 完全平方数](#4. 完全平方数)
- [III. 二维费用的背包问题](#III. 二维费用的背包问题)
- - [1. 一和零](#1. 一和零)
  - [2. 盈利计划](#2. 盈利计划)
三、看起来是背包其实不是---组合总数IV
四、卡特兰数------不同的二叉搜索树

一、双数组DP

1. 最长公共子序列

题目链接

解决双数组DP，我们一般有两个步骤

选取第一个字符串的[0,i]区间进行研究，选取第二个字符串的[0,j]区间进行研究
根据题目要求来确定我们的状态表示

这道题非常经典，是解决双数组DP的模板题

这样我们就可以定义出dp[i][j]，表示s1字符串的[0,i]区间和s2字符串的[0,j]区间内的所有子序列中最长公共子序列长度

这样，我们来确定我们的状态转移方程，老样子还是根据我们最后一个位置状态去划分问题

注意，我们求的是子序列（不一定是一段连续区间）

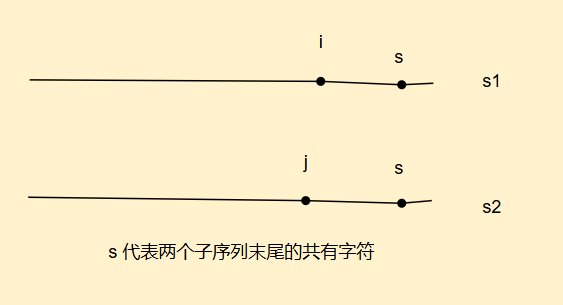
如果两个子序列要是相同的，则它们的末尾字符一定要是相同的才可以

换句话来说，它们都是以字符s为结尾的

好，因此如果s1[i] == s2[j]，那我们可以在[0,i-1]和[0,j-1]区间内找一个最长的的公共子序列，再加上字符s1[i]或s2[j]（也就是dp[i-1][j-1]+1），这样就可以拼成一个更长的公共子序列

如果s1[i] != s2[j]，这就说明最长公共子序列不是同时以i,j位置字符为结尾。那我们可以去s1[0,i-1]和s2[0,j]区间内寻找，或者去s1[0,i]和s2[0,j-1]区间内寻找，又或者可以去s1[0,i-1]和s2[0,j-1]区间内寻找。我们只需要取这三种情况最大值就好

但是聪明的你一定发现了，我们区间是不是存在重复性，你看我们的[0,i-1]和[0,j]是不是包含了[0,i-1]和[0,j-1]这个区间，我们的[0,i]和[0,j-1]是不是又包含了[0,i-1]和[0,j-1]这个区间，因此我们第三种情况就可以略去了

你说，如果我不优化，就取三种情况最大值，代码会不会有错，我的答案是不会，注意我们求的是长度，不是个数，我们长度取得最大值往往只有一种结果，但是我们个数取得最大值则一定会有重复的现象，大家可以自己思考下

好我们再来看初始化，子序列是包含空串的，因此空串也要考虑

那我们为了避免填表的时候越界，引入虚拟边界，我们再来看虚拟边界我们要填什么值

为了避免和原字符错位的下标映射，我们可以再两个字符串开头加入空白字符，让字符串下标和dp数组下标对齐，方便映射填表

因为我们每一次都需要上一行的值和当前行左边的值，因此我们是从上到下，从左到右填表

最后我们返回dp表右下角的值就好

java 复制代码

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        //对于字符串的问题，我们可以进行特殊的处理，让dp填表的时候不用去处理越界问题
        int length1 = text1.length();
        int length2 = text2.length();
        text1 = " "+text1;
        text2 = " "+text2;
        char [] t1 = text1.toCharArray();
        char [] t2 = text2.toCharArray();
        //dp[i][j]表示t1的[0,i]和t2[0,j]区间内的最长公共子序列的长度
        int [][] dp = new int[length1+1][length2+1];
        //填表
        for(int i = 1;i <= length1;i++){
            for(int j = 1;j <= length2;j++){
                //比较字符
                if(t1[i] == t2[j]){
                    //此时两个公共子串的结尾字符已经相同，仅需在[0,i-1]和[0,j-1]区间内寻找最长公共子序列即可
                    dp[i][j] = dp[i-1][j-1]+1;
                }else{
                    //此时说明不相等，那我们要在三个区间内部寻找
                    //[0,i-1]&&[0,j]，[0,i]&&[0,j-1]，[0,i-1][0,j-1]
                    //但是第三种情况已经被前面两种情况包含了，因此不用重复考虑
                    dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);
                }
            }
        }
        return dp[length1][length2];
    }
}

2. 不相交的线

题目链接

这一题乍一看没思路，是因为这一题不好转化为我们的动态规划问题

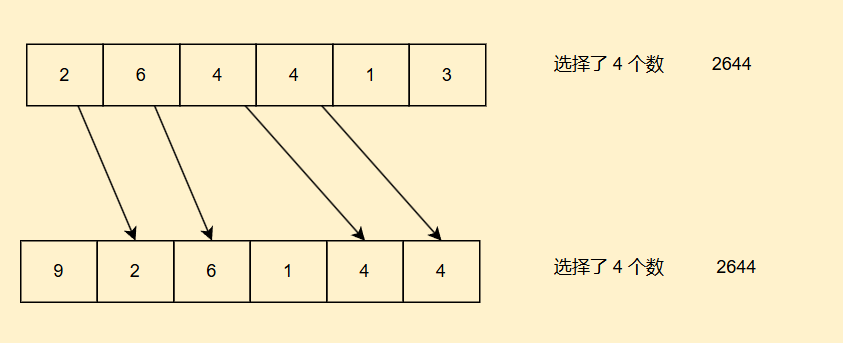
你看到规律了吗，我们是不是都选择了两个数组公共的部分，这不就是上一题的最长公共子序列问题吗！

java 复制代码

class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        //最长公共子序列套壳
        int length1 = nums1.length;
        int length2 = nums2.length;
        //dp[i][j]表示s1[0,i]和n2[0,j]区间内的最长公共子序列长度
        int [][] dp = new int[length1+1][length2+1];
        for(int i = 1;i <= length1;i++){
            for(int j = 1;j <= length2;j++){
                if(nums1[i-1] == nums2[j-1]){
                    dp[i][j] = dp[i-1][j-1]+1;
                }else{
                    dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);
                }
            }
        }
        return dp[length1][length2];
    }
}

3. 不同的子序列

题目链接

这一题我们要这样定义状态表示，还是使用区间表示

题目要我们寻找在s字符串的所有子序列中包含多少个t这个字符串

那我们就要拆分，研究在s的[0,j]的这个区间的所有子序列（不连续区间）寻找t的[0,i]区间子串

什么意思，比如我们的s = abad，t = abc

我们研究s的aad这个子序列，寻找包含了多少个t的a这个子串

因此我们的状态表示就是dp[i][j]，表示在s的[0,j]区间内的所有子序列（不一定是连续的区间）中寻找包含多少个t的[0,i]区间的这个子串（连续区间）

这样我们就可以划分s子序列中的最后一个位置字符状态

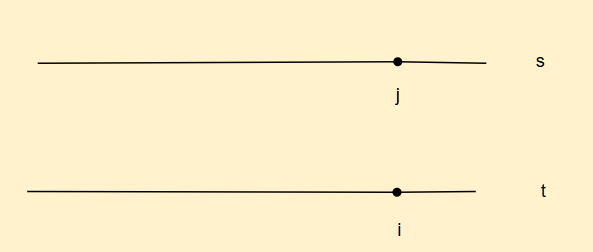
如果s子序列的最后一个字符不和t的[0,i]区间这个子串的最后一个字符相同，那我们可以去j位置前一个字符找找看，此时就是dp[i][j-1]

反之，如果我们s子序列的最后一个字符和我们t的[0,i]区间这个子串最后一个字符是相同的，那我们最后一个字符就不用比较了，那我们就可以去i位置和j位置前面的字符看看有几个匹配的，如果存在很多个，我们加上就好

java 复制代码

dp[i][j] = dp[i][j-1];
if(s[j] == t[i]){
	dp[i][j] += dp[i-1][j-1];
}

大家可以根据状态表示多体会下

我们还是引入空字符进行辅助，而且引入虚拟边界，我们思考下边界值都填啥

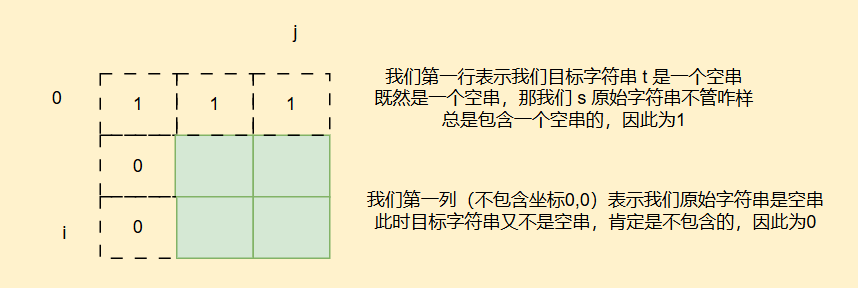
我们填表根据方程得知要从上往下，从左往右填表，最后返回dp[t.length()][s.length()]

其实本题本质上是一种状态拆分的思想，既然一次性研究大的不行，那我们就从小范围开始研究

java 复制代码

class Solution {
    public int numDistinct(String s, String t) {
        int length1 = s.length();
        int length2 = t.length();
        //特殊处理下字符串
        s = " "+s;
        t = " "+t;
        char [] ss = s.toCharArray();
        char [] tt = t.toCharArray();
        //dp[i][j]表示s[0][j]的所有子序列中包含多少个t[0][i]的这个子串
        //行表示t字符串，列表示s字符串
        int [][] dp = new int[length2+1][length1+1];
        //初始化第一行，因为dp[0]表示目标串t是空串，在s中必然是有一个空子串的
        Arrays.fill(dp[0],1);
        //填表，i表示t字符串，j表示i字符串
        for(int i = 1;i <= length2;i++){
            for(int j = 1;j <= length1;j++){
                dp[i][j] = dp[i][j-1];
                if(ss[j] == tt[i]){
                    dp[i][j] += dp[i-1][j-1];
                }
            }
        }
        return dp[length2][length1];
    }
}

4. 通配符匹配

题目链接

这一题难就难在状态转移方程推导困难

我们先来解释下这一题是什么意思

比如s=adceb，p=*a*b

此时我可以让第一个*匹配掉s的空串，此时s=adceb，p=a*b

再让p的a字符匹配s的a字符，此时s=dceb，p=*b

此时再让p的·*匹配s的dce字符，此时s=b，p=b

此时再互相匹配，最终匹配完毕

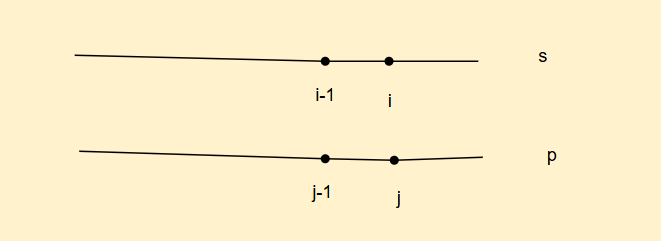
因此我们可以这样定义状态表示，dp[i][j]表示p字符串的[0,j]区间内的子串能否匹配s字符串的[0,i]区间内的子串，能就是true，否则就是false

好，我们接着来分析状态转移方程，根据最后一个位置情况划分问题

若p[j]是一个非* ?的普通字符，如果想要匹配成功，那么要保证s[i] == p[j]，并且s[i-1],p[j-1]也是互相匹配的，这个正好就是我们状态表示dp[i-1][j-1]。只有当两个条件都成立了，dp[i][j]才是true

若p[j]是一个?，因为它可以匹配任何一个字符，因此此时s[i]和p[j]自然就匹配了，那我们还是看看s[i-1],p[j-1]是否匹配就好

接下来这个*是最麻烦的，若p[j]是一个*

匹配空串，此时因为*已经被使用了，并且匹配的事s[i]的空串，因此我们要去s[0,i]区间和p[0,j-1]区间内看看，正好就是我们状态表示dp[i][j-1]

匹配一个字符，此时就是dp[i-1][j-1]

匹配两个字符，此时就是dp[i-2][j-1]

...

此时我们发现有非常多的状态表示，那我们要通过一种手段，把无限的状态表示替换成有限的状态表示，我们首先来看我们的dp[i][j]方程
dp[i][j] = dp[i][j-1] || dp[i-1][j-1] || dp[i-2][j-1] || dp[i-3][j-1] .........

此时聪明的你发现j-1是一直不会变化的，因此你想到我把·dp[i][j]中的i替换成i-1，我们发现我们的方程
dp[i-1][j] = dp[i-1][j-1] || dp[i-2][j-1] || dp[i-3][j-1] || dp[i-4][j-1]，是不是和dp[i][j]有重叠部分啊

因此我们可以直接dp[i][j] = dp[i][j-1] || dp[i-1][j]

这本质上是一种数学代换思想，具体严格证明可以去网上搜索

其实如果数学代换你不能理解，我们还有一种感性的理解，你看我们*是不是可以匹配很多字符啊，当我们匹配完一个字符后，我们不能消除*，我们要看s[i-1]区间和p[0,j]区间是否匹配，这不就是我们状态表示dp[i-1][j]吗

上面两种方式大家伙如果还是不能理解的话，可以去看看这个题题解或者是借助工具，毕竟书面形式肯定没有视频形式传递的效果好

我们初始化还是引入空字符进行辅助，并且还是引入虚拟边界

当然，我们要注意边界的初始值，这样保证后续填表正确

因为我们每次填表都要依赖上一行和当前行左边的值，因此我们是从上到下，从左到右填表，最终返回dp表右下角值就好

java 复制代码

class Solution {
    public boolean isMatch(String s, String p) {
        int lenS = s.length();
        int lenP = p.length();
        //特殊处理下字符串，方便填表
        s = " "+s;
        p = " "+p;
        char [] ss = s.toCharArray();
        char [] pp = p.toCharArray();
        //dp[i][j]表示s的[0,i]和p[0,j]能否进行匹配
        //横坐标表示s字符串，纵坐标表示p字符串
        boolean [][] dp = new boolean[lenS+1][lenP+1];
        //第一个位置是true，因为空串可以相互匹配
        dp[0][0] = true;
        //初始化要注意，对于我们dp表，第一行表示s为空串，如果p也是空串，则可以进行匹配
        //同时，如果p开头带有"*"则可以进行匹配，直到遇到第一个不为"*"的字符
        //比如s="",p="**s***"，此时p的前两个字符可以匹配，其他字符则匹配不了，对应的dp表第一行就是
        //true true false false false
        for(int i = 1;i <= lenP;i++){
            //注意遇到第一个不是*字符就要跳出
            if(pp[i] == '*'){
                dp[0][i] = true;
                continue;   
            }
            break;
        }
        //进行填表，i表示字符串s索引，j表示字符串p索引
        for(int j = 1;j <= lenP;j++){
            for(int i = 1;i <= lenS;i++){
                //判断p[j]字符的情况
                if(pp[j] == '?'){
                    //此时p[j]匹配掉了s[i]的一个字符
                    dp[i][j] = dp[i-1][j-1]; 
                }else if(pp[j] == '*'){
                    //此时这个*要讨论的就有很多
                    //如果只是暴力的枚举所有情况，如下
                    //匹配s中的一个空串，此时这个*相当于用掉了，则dp[i][j] = dp[i][j-1]
                    //综合地，匹配空串，匹配s中的一个字符，两个字符，三个字符......
                    //则dp[i][j] = dp[i][j-1] || dp[i-1][j-1] || dp[i-2][j-1] || dp[i-3][j-1] ......
                    //那如果我们把dp[i][j]中的i-1，然后再看这个表达式
                    //dp[i-1][j] = dp[i-1][j-1] || dp[i-2][j-1] || dp[i-3][j-1] ......
                    //此时你会惊奇的发现，我的两个表达式有重复部分，那我是不是可以进行归纳总结，直接
                    //dp[i][j] = dp[i][j-1] || dp[i-1][j]就好了，这样就涵盖了所有情况
                    //____________________________________________________________________
                    //我们还有另一种想法，还是一样的，如果匹配s的一个空串，则还是dp[i][j-1]
                    //但是除此以外，不管匹配多少个字符，我们的*都不消去
                    //这样dp[i][j] = dp[i][j-1] || dp[i-1][j] || dp[i-2][j] || dp[i-3][j] .....
                    //一直向下传递，其实也涵盖了所有情况，因此我们得出的结论还是
                    //dp[i][j] = dp[i][j-1] || dp[i-1][j]
                    dp[i][j] = dp[i-1][j] || dp[i][j-1];
                }else{
                    //此时说明是普通字符，判断字符相不相等
                    dp[i][j] = pp[j] != ss[i] ? false : dp[i-1][j-1];
                }
            }
        }
        return dp[lenS][lenP];
    }
}

5. 正则表达式匹配

题目链接

这道题其实就是上一道题的衍生版本，我们还是先来解析下题目，注意*不能单独存在，要和前面结合，表示可以匹配前面字符0,1,2...次

若s=aa,p=a*，此时*可以匹配多个字符a，为true

若s=ab,p=.*，此时.可以匹配任意字符，加上*，此时p可以匹配多个任意字符

若s=aab,p=d*a*.，先让d*匹配s空串（也就是说我和前面的字符d结合，但是我不匹配任何d字符），此时s=aab,p=a*.，再让a*匹配aa，此时s=b,p=.，再让.匹配b，因此为true

并且在题目的提示中，我们也看见，s中只有小写字母，p中才有通配符，并且每个*前面不会再出现*

因此我们这样来确定状态表示，dp[i][j]表示p字符串[0,j]区间这个子串能否匹配s字符串的[0,i]区间这个子串

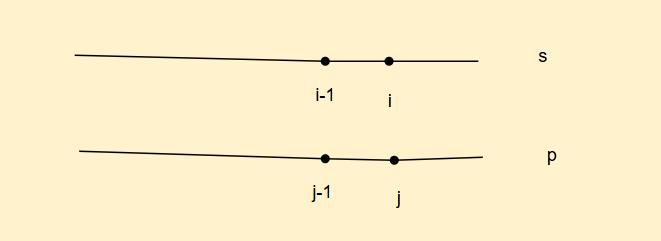
因此我们来推导状态转移方程，根据p[j]最后一个字符划分情况

若p[j]为小写字符，要想匹配首先要保证p[j] == s[i]，并且[0,i-1]和[0,j-1]区间内要匹配，因此就是dp[i-1][j-1]

若p[j]为.，此时可以匹配s中任意一个字符，因此就是dp[i-1][j-1]

最麻烦的还是*，分情况讨论，注意我们*无法单独使用，要和前面字符结合

若p[j-1]为.，此时的组合就是.*，它可以匹配空串，一个字符，两个字符，三个字符...

如果匹配为空串，则我们就要看看s的[0,i]区间和p的[0,j-2]区间，就是dp[i][j-2]

如果匹配一个字符，则是dp[i-1][j-2]。如果匹配两个字符，则是dp[i-2][j-2]...

和上一题优化思想一样，我们可以直接总结为dp[i][j] = dp[i][j-2] || dp[i-1][j]
若p[j-1]为小写字符，此时组合就是(小写字符x)*，他可以匹配空串，一个字符x，两字符x，三个字符x

如果匹配为空串，则是dp[i][j-1]

如果匹配多个字符，并且保证p[j-1] == s[i]，此时还是和上一题优化思想一样，我们直接总结为dp[i][j] = dp[i-1][j]

综上所述，我们状态转移方程就是

复制代码

若p[j] == s[i] || p[j] = '.'
则dp[i][j] = dp[i-1][j]

若p[j] == '*'，则必然可以匹配空串  
如果判断前面的字符则  
dp[i][j] = dp[i][j-2] || (p[j-1] == '.' || p[j-1] == s[i]) && dp[i-1][j]

对于初始化方面，我们引入空字符进行辅助，并且加入虚拟边界

因为我们填表都要上一行值和当前行左边值，因此是从上到下，从左到右填表，最后返回dp表右下角值

java 复制代码

class Solution {
    public boolean isMatch(String s, String p) {
        int lenS = s.length();
        int lenP = p.length();
        //添加辅助空串，便于填表
        s = " "+s;
        p = " "+p;
        char [] ss = s.toCharArray();
        char [] pp = p.toCharArray();
        //dp[i][j]表示s的[0,i]和p的[0,j]区间内部是否能进行匹配
        //其中行表示字符串s，列表示字符串p
        boolean [][] dp = new boolean[lenS+1][lenP+1];
        //dp[0][0]为true，因为空串可以相互匹配
        dp[0][0] = true;
        //初始化第一行，第一行表示我们的s字符串是空串
        //如果我们的p字符串的偶数下标存在*通配符，则可以进行空串匹配
        for(int i = 2;i <= lenP;i+=2){
            //注意偏移后的字符从1开始，则其偶数位自然从2开始哦！
            //遇到偶数下标第一个非*就要立马跳出
            if(pp[i] == '*'){
                dp[0][i] = true;
                continue;
            }
            break;
        }
        //填表
        for(int j = 1;j <= lenP;j++){
            for(int i = 1;i <= lenS;i++){
                //判断字符情况
                if(pp[j] == '*'){
                    //默认空串都可以匹配
                    //多个字符串，但是要注意如果是".*"和"字符*"几种情况
                    dp[i][j] = dp[i][j-2] || (pp[j-1] == ss[i] || pp[j-1] == '.') && dp[i-1][j];
                }else if(pp[j] == '.'){
                    dp[i][j] = dp[i-1][j-1];
                }else{
                    dp[i][j] = pp[j] != ss[i] ? false : dp[i-1][j-1]; 
                }
            }
        }
        return dp[lenS][lenP];
    }
}

6. 交错字符串

题目链接

这一题说人话就是把s1和s2切成若干份进行拼接，看到底能不能拼成s3

因此我们这样定义状态表示，如果我们s1选了[0,i]区间，s2选了[0,j]区间，要想拼成s3，则我们s3区间就是[0,i+j]。当然这一题为了下标映射方便，我们都加入空字符辅助，这样三个字符串下标都从1开始计算了
dp[i][j]表示s1的[1,i]区间和s2的[1,j]区间能否拼接成s3的[1,i+j]区间的这个子串

因此我们的状态转移方程就是根据最后一个位置情况划分

如果我们s1[i]位置字符或者是s2[j]位置字符都不和s3[i+j]位置字符匹配，那么dp[i][j] = false

若s1[i] == s3[i+j]，此时研究s1的[1,i-1]区间和s2的[1,j]区间能否拼成s3的[1,i+j-1]区间的这个子串，因此就是dp[i-1][j]

若s2[j] == s3[i+j]，同理得出dp[i][j-1]

我么只需要两种情况有一种情况成立就好

我们在来看初始化方面，引入虚拟边界

我们从上到下，从左到右填表，最后返回dp表右下角值

java 复制代码

class Solution {
    public boolean isInterleave(String s1, String s2, String s3) {
        int length1 = s1.length();
        int length2 = s2.length();
        //处理边界条件
        if(length1+length2 != s3.length()){
            //长度都不同，怎么拼
            return false;
        }
        //引入空串进行辅助填表
        s1 = " "+s1;
        s2 = " "+s2;
        s3 = " "+s3;
        char [] ss1 = s1.toCharArray();
        char [] ss2 = s2.toCharArray();
        char [] ss3 = s3.toCharArray();
        //dp[i][j]表示s1的[1,i]区间的子串和s2的[1,j]区间内的子串能否拼接s3[1,i+j]区间的字符串
        boolean [][] dp = new boolean[length1+1][length2+1];
        //注意都是空串也可以匹配
        dp[0][0] = true;
        //初始化，对于dp表的第一行m表示s1为空串，我们要看s2的部分子串是否能和s3匹配
        //第一列同理，此时s2为空串，我们要看s1的部分子串是否能和s3匹配
        for(int j = 1;j <= length2;j++){
            //字符相等才匹配，此时s1为空串
            if(ss2[j] == ss3[j]){
                dp[0][j] = true;
                continue;
            }
            break;
        }
        for(int i = 1;i <= length1;i++){
            //字符相等才匹配，此时s2为空串
            if(ss1[i] == ss3[i]){
                dp[i][0] = true;
                continue;
            }
            break;
        }
        //填表
        for(int i = 1;i <= length1;i++){
            for(int j = 1;j <= length2;j++){
                //看看i和j下标哪个位置元素和i+j位置元素相同
                //只用考虑一种情况就好
                dp[i][j] = (ss1[i] == ss3[i+j] && dp[i-1][j]) || (ss2[j] == ss3[i+j] && dp[i][j-1]);
            }
        }
        return dp[length1][length2];
    }
}

7. 两个字符串最小ASCII删除和

题目链接

这一题要求我们的最小删除和，使得两个字符串相同，我们再想一想，最后是不是就是要的两个字符串的共有部分

那问题是不是就可以转换成两个字符串的公共子序列ASCII码值最大的情况，最后返回结果的时候只需要把两个字符串的ASCII码值和求出来，减去两倍的公共子序列最大和，剩下的就是两个字符串非共有部分，不就是我们要求的吗

因此我们dp[i][j]表示s1的[0,i]区间和s2的[0,j]区间的所有子序列中的公共子序列ASCII最大和

我们根据最后一个位置状态推到房产，有四种情况

s1子序列中以s1[i]字符为结尾，s2子序列中以s2字符为结尾

s1子序列中不以s1[i]字符为结尾，s2子序列中以s2字符为结尾

s1子序列中以s1[i]字符为结尾，s2子序列中不以s2字符为结尾

s1子序列中不以s1[i]字符为结尾，s2子序列中不以s2字符为结尾
情况一：要保证s1[i] == s2[j]，则为dp[i-1][j-1]+s1[i]（s2[j]也可以）（ASCII码值）

情况二/情况三：我们发现我们状态表示是说的所有的子序列，因此情况二和情况三就包含了情况四（我们之前题有分析过类似的情况），因此就取情况二和情况三的最大值，为Math.max(dp[i-1][j],dp[i][j-1])

我们再来看初始化，引入空字符，引入虚拟边界

我们从上往下，从左往右填表，最后返回的时候不要忘记return 两个字符串ASCII码值-2dp表右下角值

java 复制代码

class Solution {
    public int minimumDeleteSum(String s1, String s2) {
        //这一题我们可以转换成求两个字符串的最长公共子序列的ASCII码和
        //再用两个字符串的ASCII码和减去2公共子序列ASCII码和就还
        int length1 = s1.length();
        int length2 = s2.length();
        //添加辅助字符辅助填表
        s1 = " "+s1;
        s2 = " "+s2;
        char [] ss1 = s1.toCharArray();
        char [] ss2 = s2.toCharArray();
        //dp[i][j]表示s1的[0,i]和s2[0,j]区间的最长公共子序列
        int [][] dp = new int[length1+1][length2+1];
        //跟踪求和
        int countForASCII = 0;
        for(int i = 1;i <= length1;i++){
            countForASCII += ss1[i];
        }
        for(int i = 1;i <= length2;i++){
            countForASCII += ss2[i];
        }
        //填表
        for(int i = 1;i <= length1;i++){
            for(int j = 1;j <= length2;j++){
                //分情况讨论
                dp[i][j] = Math.max(dp[i][j-1],dp[i-1][j]);
                //如果字符还相同
                if(ss1[i] == ss2[j]){
                    dp[i][j] = Math.max(dp[i-1][j-1]+ss1[i],dp[i][j]);
                }
            }
        }
        return countForASCII-2*dp[length1][length2];
    }
}

8. 最长重复子数组

题目链接

注意子数组不是子序列，它在数组中是一片连续的区间

注意我们如果用一维dp表，比如dp[i]表示[0,i]任意一段区间内的所有子数组中的重复字数组的最长长度

那么如果这个重复子数组在区间[i-12,i-5]，由于子数组要求是连续区间，我们i位置元素是不能直接添加到这个子数组后面的（不是子序列）

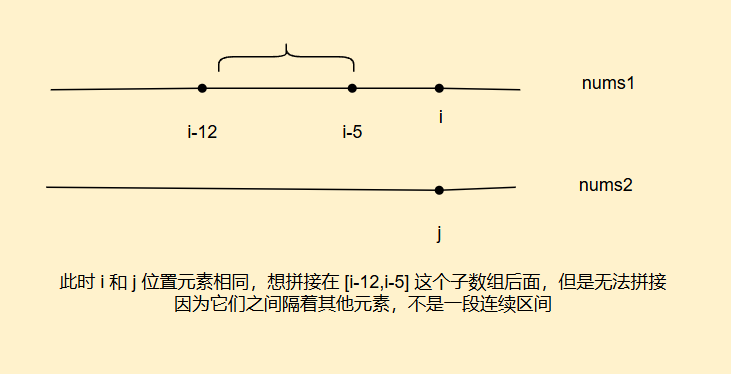
因此我们这样定义，dp[i][j]表示在nums1中以i位置结尾且nums2中以j位置为结尾的两个子数组中（相当于两个子数组末尾元素固定了）最长重复子数组长度

数组末尾元素固定了，就代表我们后续元素可以在此基础上进行跟随

因此dp[i-1][j-1]这个状态表示，隐含的就是固定了i-1和j-1的元素，我们只需要判断是否跟随到i-1和j-1元素之后就好

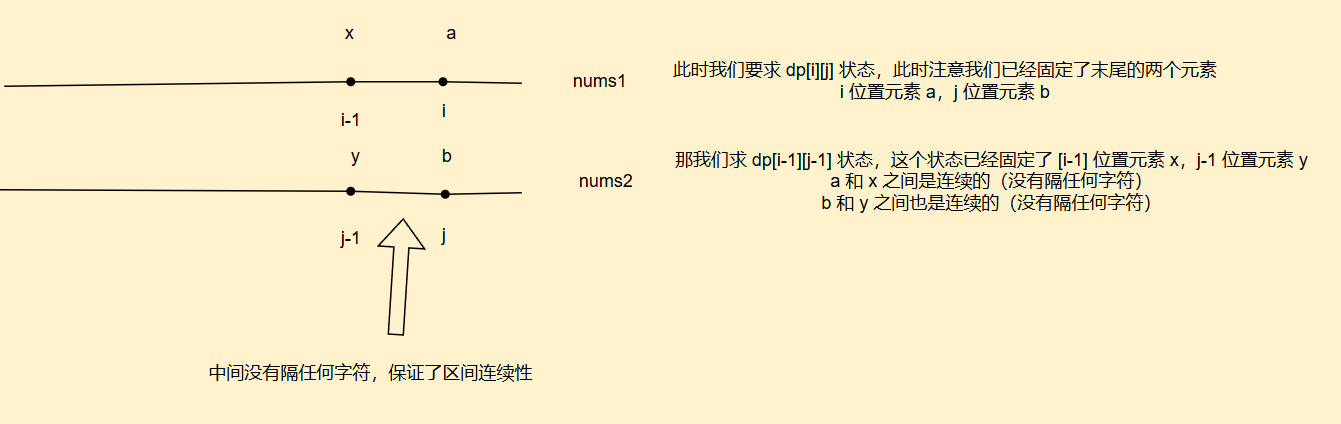
因此我们的状态转移方程就是dp[i][j] = nums1[i-1] == nums2[j-1] ? dp[i-1][j-1]+1 : 0;

因此如果我们a和b字符不相等，那么连续区间就从这里断开了，后面都要重新计算

我们初始化还是引入虚拟边界

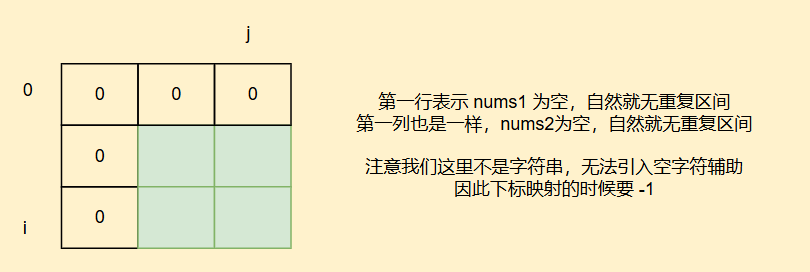
我们从上到下填表就好，最后返回dp表最大值就好

java 复制代码

class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        int length1 = nums1.length;
        int length2 = nums2.length;
        //dp[i][j]表示以nums1[i]元素为结尾并且和nums2[j]元素为结尾的子数组中最长重复子数组长度
        int [][] dp = new int[length1+1][length2+1];
        //跟踪最大值
        int ret = 0;
        //填表
        for(int i = 1;i <= length1;i++){
            for(int j = 1;j <= length2;j++){
                dp[i][j] = nums1[i-1] == nums2[j-1] ? dp[i-1][j-1]+1 : 0;
                ret = Math.max(dp[i][j],ret);
            }
        }
        return ret;
    }
}

二、背包问题

背包问题实质上就是什么，就是说你面前有一堆物品，它们有各种的属性比如体积、价值，你要挑选几个物品放入你的背包里，背包有一定属性比如容量

你要在题目各种要求（比如不能超过背包容积，或者是恰好装满背包）下求出最大价值

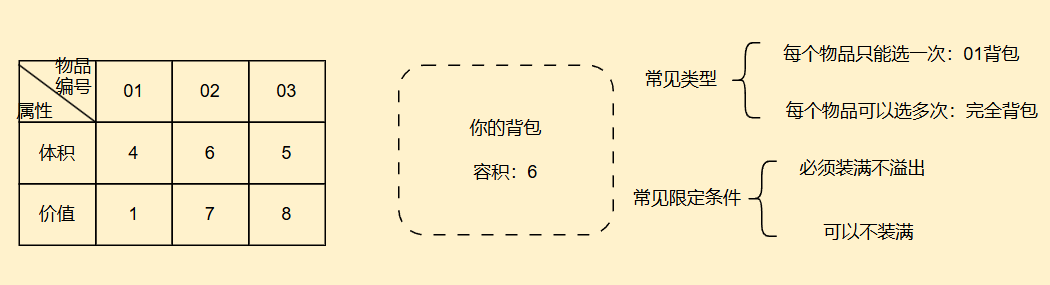
I. 01背包问题

1. 模板题

题目链接

这一题我们题目解析可以看到题目示例中是有3个物品，背包大小是5，并且每个物品只能选一次

为了做题方便，我们让物品编号从1开始便于填表

可以看到题目中分了两个子问题装满和不一定装满，注意装满这种情况可能不存在，要进行特判

我们先看背包不装满情况

我们可以这样定义状态表示
dp[i][j]表示从前i个物品中挑选，总体积不超过j的所有选择方法中的最大价值

因此我们这样定义状态转移方程，根据最后一个位置情况划分，w表示价值，v表示体积

不挑选第i个物品，此时就是dp[i-1][j]
如果挑选第i个物品，那我们挑选之前，是不是要先给i物品留位置，但是注意j-v[i]可能不存在，因为可能这个物品体积太大了直接把背包撑爆了。因此我们要特判j >= v[i]，也就是说要让背包剩余空间大于我们要挑选的这个物品体积，你才放得下，因此是dp[i-1][j-v[i]]+w[i]

因此我们初始化还是引入虚拟边界

我们每次都是需要左上角的值，因此我们从上往下填表就好。最后返回dp表右下角值

我们再来看看背包一定要装满的情况

我们可以这样定义状态表示
dp[i][j]表示从前i个物品中挑选总体积恰好为j的所有选择方法中的最大价值

为了方便区分，我们使用-1表示状态不存在的情况，这样在最后返回的时候进行判断就好了，避免和边界初始值0混淆

不挑选i物品，那么就是dp[i-1][j]
挑选i物品，除了要预留空间以外，我们还要保证dp[i-1][j-v[i]]这个状态要存在，可以自己对着状态表示体会下，只有其不为-1的时候我们才放入我们的物品i。换句话来说，就是在放入该物品之前，可能不存在这种背包状态

我们再来看初始化，还是引入虚拟边界

我们从上往下填表，最后返回dp表右下角值就好

java 复制代码

import java.util.*;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    static int capacity;//背包容量
    static int count;//物品个数
    static int [] v;//体积
    static int [] w;//价值
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        count = in.nextInt();
        capacity = in.nextInt();
        v = new int[count+1];
        w = new int[count+1];
        //使用for循环精准读取count组物品数据，避免无限读取
        for(int sign = 1;sign <= count;sign++) {
            int a = in.nextInt();
            int b = in.nextInt();
            v[sign] = a;
            w[sign] = b;
        }
        //背包不满
        int ret1 = notFilled();
        //背包满
        int ret2 = filled();
        //打印结果
        System.out.println(ret1);
        System.out.println(ret2);
    }

    private static int notFilled(){
        //定义dp表，dp[i][j]表示从前i个物品中选取体积不超过j的最大价值，不能超过背包容量
        int [][] dp = new int[count+1][capacity+1];
        //填表
        for(int i = 1;i <= count;i++){
            //j表示当前考虑的背包容量（j），能否装得下第i个物品（v[i]）
            for(int j = 0;j <= capacity;j++){
                //挑选/不挑选i物品
                dp[i][j] = dp[i-1][j];//不挑选
                if(j >= v[i]){
                    //判断再决定是否挑选
                    dp[i][j] = Math.max(dp[i][j],dp[i-1][j-v[i]]+w[i]);
                }
            }
        }
        return dp[count][capacity];
    }

    private static int filled(){
        //定义dp表，dp[i][j]表示从前i个物品中选取体积恰好为j的最大价值，同样也不能超过背包容量
        int [][] dp = new int[count+1][capacity+1];
        //初始化，由于不选择物品怎么样也达不到超过1的容量，初始化为-1
        for(int i = 1;i <= capacity;i++){
            dp[0][i] = -1;
        }
        //填表
        for(int i = 1;i <= count;i++){
            for(int j = 0;j <= capacity;j++){
                dp[i][j] = dp[i-1][j];//不挑选
                //如果选择i物品，要确保选i之前的空间里存在最大价值（不能为-1）
                //并且还要确保有足够位置
                if(j >= v[i] && dp[i-1][j-v[i]] != -1){
                    dp[i][j] = Math.max(dp[i][j],dp[i-1][j-v[i]]+w[i]);
                }
            }
        }
        //判断下是不是-1的情况
        return dp[count][capacity] == -1 ? 0 : dp[count][capacity];
    }
}

我们还可以进行空间上的优化，利用滚动数组

不知道你是否发现，我们状态转移方程，每次取得都是上一行的状态，比如我填第三行值，我只需要第二行值就好，第一行我就不需要了

因此我们可以优化为只有两行的dp表

那我们可不可以再优化，可以，我们只要一行就好，为什么？

"★= 当前要填的 dp [j]，🚩= 需要用到的 dp [j-v [i]]（上一行的旧值）"

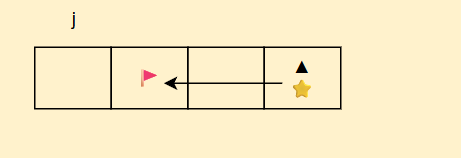
如果我们想填⭐️这个位置状态，一般来说要依赖上一行和当前行左边的值，但是上一行的状态就在我们当前行存着

这样，如果我们从左往右填表，当我们去取🚩这个状态的时候，并不是最开始的值，因为从左往右填表过程中会把🚩这个位置状态更新，因此我们要从右往左填表，保证我们⭐️去取得🚩状态的时候，是最开始的状态

同时，我们在第二层循环j判断的时候，顺便把j >= v[i]这个条件加上就好

并且我们滚动数组不用考虑不选的情况，因为已经存好了，因为我们当前位置的值就是不选当前物品时候的值

java 复制代码

import java.util.*;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    static int capacity;//背包容量
    static int count;//物品个数
    static int [] v;//体积
    static int [] w;//价值
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        count = in.nextInt();
        capacity = in.nextInt();
        v = new int[count+1];
        w = new int[count+1];
        //使用for循环精准读取count组物品数据，避免无限读取
        for(int sign = 1;sign <= count;sign++) {
            int a = in.nextInt();
            int b = in.nextInt();
            v[sign] = a;
            w[sign] = b;
        }
        //背包不满
        int ret1 = notFilled();
        //背包满
        int ret2 = filled();
        //打印结果
        System.out.println(ret1);
        System.out.println(ret2);
    }

    private static int notFilled(){
        //定义dp表，dp[j]表示从前i个物品中选取体积不超过j的最大价值，不能超过背包容量
        //滚动数组优化一：一维化
        int [] dp = new int[capacity+1];
        //填表
        for(int i = 1;i <= count;i++){
            //j表示当前考虑的背包容量（j），能否装得下第i个物品（v[i]）
            //滚动数组注意点：反向填表顺序
            //并且可以再做常数级别优化，遍历到了v[i]后就不用继续判断了，因为都不符合要求了，东西背包放不下
            for(int j = capacity;j >= v[i];j--){
                //挑选/不挑选i物品
                //滚动数组优化二：不用考虑不选的情况
                if(j >= v[i]){
                    //判断再决定是否挑选
                    dp[j] = Math.max(dp[j],dp[j-v[i]]+w[i]);
                }
            }
        }
        //滚动数组优化三：直接返回值
        return dp[capacity];
    }

    private static int filled(){
        //定义dp表，dp[i][j]表示从前i个物品中选取体积恰好为j的最大价值，同样也不能超过背包容量
        //滚动数组优化一：一维化
        int [] dp = new int[capacity+1];
        //初始化，由于不选择物品怎么样也达不到超过1的容量，初始化为-1
        for(int i = 1;i <= capacity;i++){
            dp[i] = -1;
        }
        //填表
        for(int i = 1;i <= count;i++){
            //滚动数组注意点：反向填表
            //并且可以再做常数级别优化，遍历到了v[i]后就不用继续判断了，因为都不符合要求了，东西背包放不下
            for(int j = capacity;j >= v[i];j--){
                //滚动数组优化二：不用考虑不选的情况
                //如果选择i物品，要确保选i之前的空间里存在最大价值（不能为-1）
                //并且还要确保有足够位置
                if(j >= v[i] && dp[j-v[i]] != -1){
                    dp[j] = Math.max(dp[j],dp[j-v[i]]+w[i]);
                }
            }
        }
        //判断下是不是-1的情况
        //滚动数组优化三：直接返回值
        return dp[capacity] == -1 ? 0 : dp[capacity];
    }
}

2. 分割等和子集

题目链接

我们用sum表示数组整体的和，那么其中一个子集的和必然是sum/2，因此我们要从原数组中找出一些数字，让这些数字的和满足sum/2

转换成01背包问题，有一个容量为sum/2的背包，现在你要选择一些数字（值代表体积），每个数字你都可以选或者是不选，你要看看能不能刚好装满你的背包

因此我们这样定义状态表示，dp[i][j]表示从前i个数中选，在所有的选择方法中看看其和能否恰好等于j

因此我们根据最后一个位置划分情况，即选货不选

不选i元素，则为dp[i-1][j]
选i元素，我们要判断j-nums[i]存不存在，因此要保证我们背包剩余空间j >= nums[i]
这两种状态只要有一种成立就好

我们再来看初始化，引入虚拟边界

我们从上往下填表就好了，最后返回dp表dp[原数组长度][sum/2]

注意，如果我们sum/2结果是一个奇数，则代表我们无法平分两半

java 复制代码

class Solution {
    public boolean canPartition(int[] nums) {
        //这一题就是转换为01背包问题，将数组按照和等分为两份，仅需看nums中的子集能否凑成sum/2计科
        int sum = 0;
        for(int num : nums){
            sum += num;
        }
        //如果是奇数直接返回false
        if(sum%2 == 1){
            return false;
        }
        int length = nums.length;
        //dp[i][j]表示从前i个数中的所有选法中能否凑成j
        boolean [][] dp = new boolean[length+1][sum];
        //初始化第一列
        for(int i = 0;i <= length;i++){
            dp[i][0] = true;
        }
        //填表
        for(int i = 1;i <= length;i++){
            for(int j = 1;j <= sum/2;j++){
                dp[i][j] = dp[i-1][j];//不选i位置数字
                //选择i位置数字，但是前提要保证选择i位置数字前要存在
                if(j >= nums[i-1]){
                    dp[i][j] = dp[i][j] || dp[i-1][j-nums[i-1]];
                }
            }
        }
        //返回值
        return dp[length][sum/2];
    }
}

空间优化版

java 复制代码

class Solution {
    public boolean canPartition(int[] nums) {
        //这一题就是转换为01背包问题，将数组按照和等分为两份，仅需看nums中的子集能否凑成sum/2计科
        int sum = 0;
        for(int num : nums){
            sum += num;
        }
        //如果是奇数直接返回false
        if(sum%2 == 1){
            return false;
        }
        int length = nums.length;
        //dp[i][j]表示从前i个数中的所有选法中能否凑成j
        boolean [] dp = new boolean[sum/2+1];
        //初始化第一列
        dp[0] = true;
        //填表
        for(int i = 1;i <= length;i++){
            for(int j = sum/2;j >= nums[i-1];j--){
                //选择i位置数字，但是前提要保证选择i位置数字前要存在，已经改到循环条件判断中了
                dp[j] = dp[j] || dp[j-nums[i-1]];
            }
        }
        //返回值
        return dp[sum/2];
    }
}

3. 目标和

题目链接

这一题就是让我们在数组中添加上正负号凑成target

那我们可以把这些数分成两部分
A部分：没有添加负号的数字，其和为a
B部分：添加了负号的数字，其绝对值的和为b

并且我们原数组的和为sum，那么就满足a+b == sum

那我们再来看，此时还满足a-b == target，因为b是我们添加了负号的数字，比如题目中的nums= 1,1,1,1,1 target=3，此时我们A部分就是1,1,1,1，B部分就是,-1
A部分和是4，B部分绝对值的和是1，此时4-1=3成立

因此对这两个式子进行联立

{ a + b = s u m a − b = t a r g e t \begin{cases} a + b = sum \\ a - b = target \end{cases} {a+b=suma−b=target

最后求的我们要选的数的和 a = ( t a r g e t + s u m ) / 2 a=(target+sum)/2 a=(target+sum)/2

转换成01背包就是，选出几个数，让它们和是 a = ( t a r g e t + s u m ) / 2 a=(target+sum)/2 a=(target+sum)/2就可以了

dp[i][j]表示从前i个数中选，总和恰好为j的选择方法数

因此我们可以推导状态转移方程，还是根据最后一个位置情况来划分

若不选择i数字，则为dp[i-1][j]
若选择i数字，前提是要保证j-nums[i]这个和要存在，再为dp[i-1][j-nums[i]]
我们只需要把以上两种情况相加就好

对于初始化，我们还是引入虚拟边界

我们从上往下填表，最后返回dp[原数组长度][(target+sum)/2]就好

java 复制代码

class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        //这一题我们转化为01背包问题
        //根据数学原理，我们设数组总和为sum
        //此时我们可以把数组的元素分成两份，一份全是正数记为a，另一份全是负数记为b
        //a+|b| = sum 且 a-|b| = target ==> a = (sum+target)/2\
        int sum = 0;
        for(int num : nums){
            sum += num;
        }
        int aim = (sum+target)/2;
        //处理边界
        if(aim < 0 || (sum+target) % 2 == 1){
            //如果是负数或者是奇数，凑不出来
            return 0;
        }
        int length = nums.length;
        //动态规划，dp[i][j]表示从前i个数中选出目标和恰好为j的选法个数
        int [][] dp = new int[length+1][aim+1];
        //初始化
        dp[0][0] = 1;
        //填表
        for(int i = 1;i <= length;i++){
            for(int j = 0;j <= aim;j++){
                dp[i][j] = dp[i-1][j];
                if(j >= nums[i-1]){
                    dp[i][j] += dp[i-1][j-nums[i-1]];
                }
            }
        }
        return dp[length][aim];
    }
}

空间优化版本

java 复制代码

class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        //这一题我们转化为01背包问题
        //根据数学原理，我们设数组总和为sum
        //此时我们可以把数组的元素分成两份，一份全是正数记为a，另一份全是负数记为b
        //a+|b| = sum 且 a-|b| = target ==> a = (sum+target)/2\
        int sum = 0;
        for(int num : nums){
            sum += num;
        }
        int aim = (sum+target)/2;
        //处理边界
        if(aim < 0 || (sum+target) % 2 == 1){
            //如果是负数或者是奇数，凑不出来
            return 0;
        }
        int length = nums.length;
        //动态规划，dp[i][j]表示从前i个数中选出目标和恰好为j的选法个数
        int [] dp = new int[aim+1];
        //初始化
        dp[0] = 1;
        //填表
        for(int i = 1;i <= length;i++){
            for(int j = aim;j >= nums[i-1];j--){
                dp[j] += dp[j-nums[i-1]];
            }
        }
        return dp[aim];
    }
}

当然这一题还有递归解法，两种递归解法

java 复制代码

class Solution {
    int targets;
    int count;
    public int findTargetSumWays(int[] nums, int target) {
        targets = target;
        //解法一：path作为参数传递
        dfs(nums,0,0);
        return count;
    }

    private void dfs(int [] array,int path,int pos){
        if(pos == array.length){
            if(path == targets){
                count++;
            }
            return;
        }
        dfs(array,path+array[pos],pos+1);
        dfs(array,path-array[pos],pos+1);
    }
}

java 复制代码

class Solution {
    int path;
    int targets;
    int count;
    public int findTargetSumWays(int[] nums, int target) {
        //path作为全局变量传递
        targets = target;
        dfs(nums,0);
        return count;
    }

    private void dfs(int [] array,int pos){
        if(pos == array.length){
            if(path == targets){
                count++;
            }
            return;
        }
        //加法
        path += array[pos];
        dfs(array,pos+1);
        path -= array[pos];

        //减法
        path -= array[pos];
        dfs(array,pos+1);
        path += array[pos];
    }
}

4. 最后一块石头重量II

题目链接

这一题我们任意石头碰撞，过程如下，石头重量都是随机的
[a,b,c,d,e] => [a,b-d,c,e] => [b-d,c-a,e] => [b-d-c+a,e] => [e-b+d+c-a]

熟悉吗，不就是目标和那道题吗，给数字加负号

因此按照那一体思想，我们把数字分成两个部分，原数组的和为sum
A部分都是正数，和为a
B部分都是负数，绝对值的和为b

题目在问的就是|a-b|最下值，假设a>b，那么就是a-b最小

要想使得a-b尽可能小，是不是要保证|a|,|b|这两个数字要非常接近，相当于各自平分原数组

因此问题就转变为，在原数组中挑出一些数，可以选或不选，目的就是让这些挑出来的数字和尽量接近sum/2

最后我们我们会得到dp[原数组长度][sum/2]，就表示a这个数，那我们b这个数就是sum-a

那我们要求的是最后剩下的一个数，我们就是让最后这两个数再次碰撞，留下最后的数，也就是|a-(sum-a)|== sum-2a == sum-2*dp[原数组长度][sum/2]

java 复制代码

class Solution {
    public int lastStoneWeightII(int[] stones) {
        //这一题可以转换成01背包问题
        //我们可以给每个数加上正号或者是负号，分成两个部分
        //要让正数部分值-负数部分绝对值尽可能的小
        //也就是在数组中选一些数，让其值尽可能接近sum/2
        int sum = 0;
        for(int num : stones){
            sum += num;
        }
        int target = sum/2;
        int length = stones.length;
        //dp[i][j]表示从前i个数组选，总和不超过j的最大和
        int [][] dp = new int[length+1][target+1];
        for(int i = 1;i <= length;i++){
            for(int j = 0;j <= target;j++){
                dp[i][j] = dp[i-1][j];
                if(j >= stones[i-1]){
                    dp[i][j] = Math.max(dp[i][j],dp[i-1][j-stones[i-1]]+stones[i-1]);
                }
            }
        }
        return sum-2*dp[length][target];
    }
}

空间优化版本

java 复制代码

class Solution {
    public int lastStoneWeightII(int[] stones) {
        //这一题可以转换成01背包问题
        //我们可以给每个数加上正号或者是负号，分成两个部分
        //要让正数部分值-负数部分绝对值尽可能的小
        //也就是在数组中选一些数，让其值尽可能接近sum/2
        int sum = 0;
        for(int num : stones){
            sum += num;
        }
        int target = sum/2;
        int length = stones.length;
        //dp[i][j]表示从前i个数组选，总和不超过j的最大和
        int [] dp = new int[target+1];
        for(int i = 1;i <= length;i++){
            for(int j = target;j >= stones[i-1];j--){
                dp[j] = Math.max(dp[j],dp[j-stones[i-1]]+stones[i-1]);
            }
        }
        return sum-2*dp[target];
    }
}

II. 完全背包

1. 模板题

题目链接

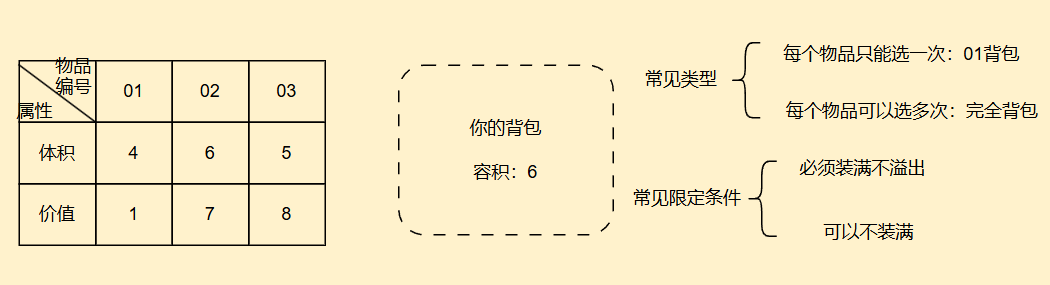
完全背包比01背包唯一的不同就是一个物品可以选择多次

我们先来看不装满的情况
dp[i][j]表示从前i个物品中挑选，总体积不超过j的所有选择方法中，获得的最大价值

因此我们状态转移方程推导就是根据最后一个位置情况划分为提，即不选或者是选几个

如果不选，则是dp[i-1][j]
如果选一个，则是dp[i-1][j-v[i]]+w[i]
如果选两个，则是dp[i-1][j-2*v[i]]+2*w[i]
如果选三个，则是dp[i-1][j-3*v[i]]+3*w[i]

发现了吗，这和我们通配符匹配那道题一样，是无限的状态，因此我们要进行有限的表示，这里就不重复推到了，我们直接得出
dp[i][j] = Math.max(dp[i-1][j],dp[i][j-v[i]])+w[i]，并且要判断j-v[i]这个状态存不存在

初始化方面，我们引入虚拟边界

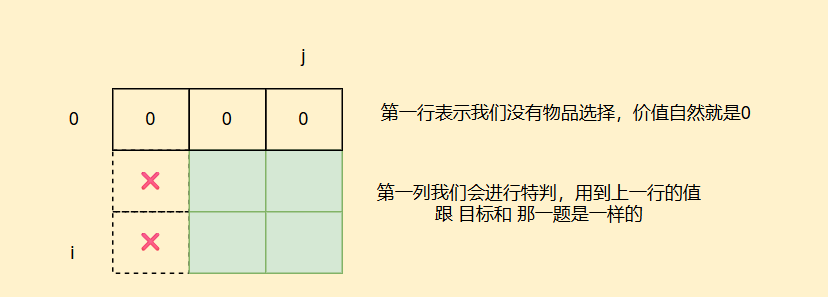
我们每一次都是需要上一行和当前行左边状态，因此是从上往下，从左右往右填表，最后返回dp表右下角值就好

我们再来看看恰好装满的情况
dp[i][j]表示从前i个物品中挑选总体积恰好为j的所有选择方法中，最大的价值

我们还是规定如果状态不存在用-1表示，区分0

我们依然可以不选或选多个

如果不选，那就是dp[i-1][j]
如果选多个，根据之前的状态总结，为dp[i][j-v[i]]+w[i]，但是前提要保证j-v[i]存在，因此要特判

初始化方面，我们引入虚拟边界

因为我们每次都要用上一行的值还有当前行左边的值，因此是从上到下，从左到右填表

最后返回的时候看看是不是-1，如果是则返回0，否则就返回我们的值

java 复制代码

import java.util.*;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    static int capacity;//背包容量
    static int count;//物品个数
    static int [] v;//物品体积
    static int [] w;//物品价值
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        count = in.nextInt();
        capacity = in.nextInt();
        v = new int[count+1];
        w = new int[count+1];
        //读取物品体积和价值，从1开始
        for(int i = 1;i <= count;i++){
            v[i] = in.nextInt();
            w[i] = in.nextInt();
        }
        //背包不装满情况
        int ret1 = notFilled();
        //背包装满情况
        int ret2 = filled();
        //打印结果
        System.out.println(ret1);
        System.out.println(ret2);
    }

    private static int notFilled(){
        //初始化dp表，dp[i][j]表示从前i个物品中的所有选法中体积不超过j的最大价值
        int [][] dp = new int[count+1][capacity+1];
        //我们无需初始化，因为对于边界情况，比如第一列，我们填表的时候会进行特殊判断
        //同时对于第一行，没有选择物品最大价值肯定是0嘛
        //------------------------------------------状态转移方程推导---------------------------------------------------------
        //如果我们不选当前i物品，那我们直接dp[i-1][j]
        //如果我们选择一个i物品，则为dp[i-1][j-v[i]]+w[i]
        //如果我们选择两个i物品，则为dp[i-1][j-2v[i]]+2w[i]
        //.........
        //如果我们选择k个i物品（不超过背包容量），则为dp[i-1][j-kv[i]]+kw[i]
        //---------------------------------------------------------------------------------------------------------------------------------------------------
        //如果我们进行等价替换，把dp[i][j]中j-->j-v[i]，则方程变为
        //dp[i-1][j-v[i]]  dp[i-1][j-2v[i]]+w[i] ......... dp[i-1][j-kv[i]]+(k-1)w[i]
        //发现没有，我们如果进行等价替换，dp[i][j-v[i]]就包括了dp[i][j]从dp[i][j-v[i]]+w[i]开始后面的值
        //并且只相差一个w[i]，我们直接加上就好了
        //因此我们最终的状态转移方程是Math.max(dp[i-1][j],dp[i][j-v[i]]+w[i])
        for(int i = 1;i <= count;i++){
            for(int j = 0;j <= capacity;j++){
                dp[i][j] = dp[i-1][j];
                //判断背包剩余空间是否符合要求
                if(j >= v[i]){
                    dp[i][j] = Math.max(dp[i][j],dp[i][j-v[i]]+w[i]);
                }
            }
        }
        return dp[count][capacity];
    }

    private static int filled(){
        int [][] dp = new int[count+1][capacity+1];
        //初始化，对于第一列我们不用管，因为我们填表会进行判断
        //但是对于第一行，第一个位置是0，因为我们没有选物品体积为0就是0
        //但是从下一个开始，我们为了区分究竟是不存在状态还是初始化状态
        //-1表示这个状态不存在，0就表示默认
        for(int i = 1;i <= capacity;i++){
            dp[0][i] = -1;
        }
        for(int i = 1;i <= count;i++){
            for(int j = 0;j <= capacity;j++){
                dp[i][j] = dp[i-1][j];
                if(j >= v[i] && dp[i][j-v[i]] != -1){
                    dp[i][j] = Math.max(dp[i][j],dp[i][j-v[i]]+w[i]);
                }
            }
        }
        return dp[count][capacity] == -1 ? 0 : dp[count][capacity];
    }
}

我们再来说说这一题使用滚动数组优化

我们直接优化为一维数组，注意我们完全背包问题要的是新的值，我们的数学归纳法总结的就是所有状态的集合，即已经更新过的dp值，和我们01背包问题要的旧值不一样，因此我们是从左往右填表

对于恰好装满问题中

注意，如果我们把dp表值全变成-0x3f3f3f3f，为什么我们第二段循环中不用判断dp[i][j-v[i]] != -1了？

它是一个足够小的伪无穷小，即使加上物品的价值w[i]，结果依然是一个极小的负数，不会变成有效状态的正数，因此最后取最大值的时候自然就不会取到这个无效的数

java 复制代码

import java.util.*;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    static int capacity;//背包容量
    static int count;//物品个数
    static int [] v;//物品体积
    static int [] w;//物品价值
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        count = in.nextInt();
        capacity = in.nextInt();
        v = new int[count+1];
        w = new int[count+1];
        //读取物品体积和价值，从1开始
        for(int i = 1;i <= count;i++){
            v[i] = in.nextInt();
            w[i] = in.nextInt();
        }
        //背包不装满情况
        int ret1 = notFilled();
        //背包装满情况
        int ret2 = filled();
        //打印结果
        System.out.println(ret1);
        System.out.println(ret2);
    }

    private static int notFilled(){
        //初始化dp表，dp[i][j]表示从前i个物品中的所有选法中体积不超过j的最大价值
        //空间优化一：一维数组
        int [] dp = new int[capacity+1];
        //我们无需初始化，因为对于边界情况，比如第一列，我们填表的时候会进行特殊判断
        //同时对于第一行，没有选择物品最大价值肯定是0嘛
        //------------------------------------------状态转移方程推导---------------------------------------------------------
        //如果我们不选当前i物品，那我们直接dp[i-1][j]
        //如果我们选择一个i物品，则为dp[i-1][j-v[i]]+w[i]
        //如果我们选择两个i物品，则为dp[i-1][j-2v[i]]+2w[i]
        //.........
        //如果我们选择k个i物品（不超过背包容量），则为dp[i-1][j-kv[i]]+kw[i]
        //---------------------------------------------------------------------------------------------------------------------------------------------------
        //如果我们进行等价替换，把dp[i][j]中j-->j-v[i]，则方程变为
        //dp[i-1][j-v[i]]  dp[i-1][j-2v[i]]+w[i] ......... dp[i-1][j-kv[i]]+(k-1)w[i]
        //发现没有，我们如果进行等价替换，dp[i][j-v[i]]就包括了dp[i][j]从dp[i][j-v[i]]+w[i]开始后面的值
        //并且只相差一个w[i]，我们直接加上就好了
        //因此我们最终的状态转移方程是Math.max(dp[i-1][j],dp[i][j-v[i]]+w[i])
        for(int i = 1;i <= count;i++){
            //常数时间优化：从左向右填表，并且不从0开始填表
            for(int j = v[i];j <= capacity;j++){
                dp[j] = Math.max(dp[j],dp[j-v[i]]+w[i]);
            }
        }
        return dp[capacity];
    }

    private static int filled(){
        int [] dp = new int[capacity+1];
        //初始化，对于第一列我们不用管，因为我们填表会进行判断
        //但是对于第一行，第一个位置是0，因为我们没有选物品体积为0就是0
        //但是从下一个开始，我们为了区分究竟是不存在状态还是初始化状态
        //-1表示这个状态不存在，0就表示默认
        for(int i = 1;i <= capacity;i++){
            //常数时间优化：配合填表形成无限小的数
            dp[i] = -0x3f3f3f3f;
        }
        for(int i = 1;i <= count;i++){
            for(int j = v[i];j <= capacity;j++){
                //为什么可以简化if判断？因为如果dp[j-v[i]]+w[i]结果足够小，比-1还小，最终结果还是dp[j]
                dp[j] = Math.max(dp[j],dp[j-v[i]]+w[i]);
            }
        }
        return dp[capacity] < 0 ? 0 : dp[capacity];
    }
}

2. 零钱兑换

题目链接

这一题我们可以非常明显的看出是一个完全背包问题
dp[i][j]表示从前i个硬币中挑选，总和恰好为j，所有的选择方法中，最少的硬币个数

因此我们这样定义状态转移方程，还是分为不选或选多个的情况，过程和模板题相同，不重复赘述
dp[i][j] = Math.max(dp[i-1][j],dp[i][j-coins[i]]+1);

当然前提还是要判断j-coins[i]要存在

对于初始化问题，我们引入虚拟边界

我们从上往下，从左往右填表就好

最后我们要判断能不能凑到，如果他是我们的0x3f3f3f3f，则代表无法凑够

否则低于这个值，就说明是能够推导出这个状态的，这跟我们表示不存在为-1是同一个道理

java 复制代码

class Solution {
    public int coinChange(int[] coins, int amount) {
        //dp[i][j]表示从前i个硬币中选，总和不超过j的最少的硬币个数
        int count = coins.length;
        int [][] dp = new int[count+1][amount+1];
        //初始化，从第一行第二个开始，要保证不参与后续计算
        for(int i = 1;i <= amount;i++){
            dp[0][i] = 0x3f3f3f3f;
        }
        //填表
        for(int i = 1;i <= count;i++){
            for(int j = 0;j <= amount;j++){
                dp[i][j] = dp[i-1][j];
                if(j >= coins[i-1]){
                    dp[i][j] = Math.min(dp[i][j],dp[i][j-coins[i-1]]+1);
                }
            }
        }
        return dp[count][amount] >= 0x3f3f3f3f ? -1 : dp[count][amount];
    }
}

空间优化版本

java 复制代码

class Solution {
    public int coinChange(int[] coins, int amount) {
        //dp[i][j]表示从前i个硬币中选，总和不超过j的最少的硬币个数
        int count = coins.length;
        int [] dp = new int[amount+1];
        //初始化，从第一行第二个开始，要保证不参与后续计算
        for(int i = 1;i <= amount;i++){
            dp[i] = 0x3f3f3f3f;
        }
        //填表
        for(int i = 1;i <= count;i++){
            for(int j = coins[i-1];j <= amount;j++){
                dp[j] = Math.min(dp[j],dp[j-coins[i-1]]+1);
            }
        }
        return dp[amount] >= 0x3f3f3f3f ? -1 : dp[amount];
    }
}

递归融合记忆化搜索版本

java 复制代码

class Solution {
    public int coinChange(int[] coins, int amount) {
        if(amount < 1){
            return 0;
        }
        int [] memory = new int[amount+1];
        int result = dfs(coins,amount,memory);
        return result == Integer.MAX_VALUE ? -1 : result;
    }

    private int dfs(int [] coins,int amount,int [] memory){
        if(amount < 0){
            return -1;
        }
        if(amount == 0){
            return 0;
        }
        //如果当前amount情况已经在记忆数组中出现过了，直接返回
        if(memory[amount] != 0){
            return memory[amount];
        }
        //选取当前amount情况中，满足要求的最少硬币个数
        int min = Integer.MAX_VALUE;
        for(int tmp : coins){
            int result = dfs(coins,amount-tmp,memory);
            if(result >= 0 && result < min){
                //加1是表示加上当前amount情况的硬币个数
                min = result+1;
            }
        }
        //记忆化数组赋值
        if(min == Integer.MAX_VALUE){
            memory[amount] = -1;
        }else{
            memory[amount] = min;
        }
        return min;
    }
}

3. 零钱兑换II

题目链接

这一题本质上就是和上一题一样，但是要注意溢出，当然Java还是不会报溢出的

java 复制代码

class Solution {
    public int change(int amount, int[] coins) {
        int count = coins.length;
        //dp[i][j]表示从前i个硬币中选择，总和恰好为j，所有的选择情况
        int [][] dp = new int[count+1][amount+1];
        dp[0][0] = 1;
        for(int i = 1;i <= count;i++){
            for(int j = 0;j <= amount;j++){
                dp[i][j] = dp[i-1][j];
                if(j >= coins[i-1]){
                    dp[i][j] += dp[i][j-coins[i-1]];
                }
            }
        }
        return dp[count][amount];
    }
}

空间优化版

java 复制代码

class Solution {
    public int change(int amount, int[] coins) {
        int count = coins.length;
        //dp[i][j]表示从前i个硬币中选择，总和恰好为j，所有的选择情况
        int [] dp = new int[amount+1];
        dp[0] = 1;
        for(int i = 1;i <= count;i++){
            for(int j = coins[i-1];j <= amount;j++){
                dp[j] += dp[j-coins[i-1]];
            }
        }
        return dp[amount];
    }
}

4. 完全平方数

题目链接

这一题说白了就是，在所有的完全平方数1,4,9,16......中挑出几个数，让其结果恰好为n，问最少挑出多少个就好

因此这一题就可以转化成完全背包问题
dp[i][j]表示从前i个完全平方数中挑选总和为j，所有的选择方法中挑选数字个数最少的情况

因此我们这么来分析我们状态转移方程，我们用i表示第1,2,3.....，其平方后就是我们的完全平方数1,4,9......

不选i²这个数，则就是dp[i-1][j]
选一个i²这个数，则就是dp[i-1][j-i²]+1
选两个i²这个数，则就是dp[i-1][j-i²*2]+2
根据之前的归纳经验，因此就是dp[i][j] = Math.min(dp[i-1][j],dp[i][j-i²]+1)，注意也是前提要保证j >= i*i

对于初始化，我们为了区分不存在和0，因此引入0x3f3f3f3f初始化边界

我们从上到下，从左到右填表，最后要注意我们返回值

比如n=13，其最大的完全平方数就是9，不可能超过13，对应9 = 3²

也就是从前三个完全平方数数选，因此返回dp[Math.sqrt(n)][n]

java 复制代码

class Solution {
    public int numSquares(int n) {
        //dp[i][j]表示从前i个完全平方数中选取，总和恰好为j，最少的数字选择个数
        int numCount = (int)Math.sqrt(n);
        int [][] dp = new int[numCount+1][n+1];
        //初始化，要保证第一行除了第一个以外的值不能参与比较，因此初始化为无穷大
        for(int i = 1;i <= n;i++){
            dp[0][i] = 0x3f3f3f3f;
        }
        for(int i = 1;i <= numCount;i++){
            for(int j = 0;j <= n;j++){
                dp[i][j] = dp[i-1][j];
                if(j >= i*i){
                    dp[i][j] = Math.min(dp[i][j],dp[i][j-i*i]+1);
                }
            }
        }
        return dp[numCount][n];
    }
}

空间优化版本

java 复制代码

class Solution {
    public int numSquares(int n) {
        //dp[i][j]表示从前i个完全平方数中选取，总和恰好为j，最少的数字选择个数
        int numCount = (int)Math.sqrt(n);
        int [] dp = new int[n+1];
        //初始化，要保证第一行除了第一个以外的值不能参与比较，因此初始化为无穷大
        for(int i = 1;i <= n;i++){
            dp[i] = 0x3f3f3f3f;
        }
        for(int i = 1;i <= numCount;i++){
            for(int j = i*i;j <= n;j++){
                dp[j] = Math.min(dp[j],dp[j-i*i]+1);
            }
        }
        return dp[n];
    }
}

III. 二维费用的背包问题

这种问题就是我们最开始在介绍背包问题时候，要考虑到体积和价值，也就是多种限制条件

我们这里列举的都是01背包类型

1. 一和零

题目链接

这道题说白了就是给定一个集合，选出一些子集，要求每个子集0不超过m个，1不超过n个，返回这些子集组合形成的更大的子集的长度（也就是个数）

dp[i][j][k]表示我从前i个字符串中挑选，字符0的个数不超过j，字符1的个数不超过k个，所有选择方法中组成更大的子集的长度（个数）

我们来分析状态转移方程，还是根据最后一个位置情况划分

若不选i位置字符串，则为dp[i-1][j][k]
如果选i位置字符串，则前提要保证j >= count0(当前字符串字符0个数) && k >= count1(当前字符串字符1个数)，则为dp[i-1][j-count0][k-count1]

对于初始化方面，我们还是引入虚拟边界

若i== 0，表示原始集合没有任何字符串，肯定凑不出来啊，为0

若j== 0 || k == 0情况会进行特判，不会使用到这种状态

我们填表的时候只需要保证i从小到大填就好，最后返回dp表dp[原数组长度][m][n]

java 复制代码

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        //使用三维dp表，dp[i][j][k]表示从前i个字符串中挑选
        //0的个数不超过j，1的个数不超过k，所有选法中，长度最长的子集
        int length = strs.length;
        int [][][] dp = new int[length+1][m+1][n+1];
        for(int i = 1;i <= length;i++){
            //统计当前字符串的0和1个数
            int count0 = 0;
            int count1 = 0;
            for(char ch : strs[i-1].toCharArray()){
                if(ch == '0'){
                    count0++;
                    continue;
                }
                count1++;
            }
            //填表
            for(int j = 0;j <= m;j++){
                for(int k = 0;k <= n;k++){
                    dp[i][j][k] = dp[i-1][j][k];
                    if(j >= count0 && k >= count1){
                        //这里+1表示长度+1
                        dp[i][j][k] = Math.max(dp[i][j][k],dp[i-1][j-count0][k-count1]+1);
                    }
                }
            }
        }
        return dp[length][m][n];
    }
}

空间优化版本

java 复制代码

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        //使用三维dp表，dp[i][j][k]表示从前i个字符串中挑选
        //0的个数不超过j，1的个数不超过k，所有选法中，长度最长的子集
        int length = strs.length;
        int [][] dp = new int[m+1][n+1];
        for(int i = 1;i <= length;i++){
            //统计当前字符串的0和1个数
            int count0 = 0;
            int count1 = 0;
            for(char ch : strs[i-1].toCharArray()){
                if(ch == '0'){
                    count0++;
                    continue;
                }
                count1++;
            }
            //填表，优化后记得改变顺序，为什么是从大到小
            //因为我们填数字的时候，是依赖i-1的数字，是更小的数字，我们要保证更小的j和k的值不能被改变
            for(int j = m;j >= count0;j--){
                for(int k = n;k >= count1;k--){
                    //这里+1表示长度+1
                    dp[j][k] = Math.max(dp[j][k],dp[j-count0][k-count1]+1);
                }
            }
        }
        return dp[m][n];
    }
}

2. 盈利计划

题目链接

这道题叽里咕噜说了那么多，就是在说每一项工作都有不同的利润，也需要不同的人数去完成，并且每个人只能参与一项工作

从所有工作中挑出一些子工作形成一个子集，要保证这个子集内所有工作总人数<=n，总利润>=m

dp[i][j][k]表示从前i个工作中挑选，总人数小于等于j，总利润大于等于k，一共有多少种选择方法

因此我们来推导状态转移方程，还是以最后一个位置状态划分

不选择第i个工作，则为dp[i-1][j][k]
选择第i个工作。对于人数，要提前预留好"空间"，则去j-g[i]寻找，如果j < g[i]，则代表这个工作要的人很多，我们现有的人数达不到要求，因此要j >= g[i]。对于利润，我们要去k-p[i]寻找，但是注意如果这个工作利润很大，导致k-p[i] < 0，虽然符合我们实际需求，但是这就导致越界了，因此我们为了不越界，结合状态表示，这种情况我们直接等于0，表示第就是这个工作利润太大了，我们前面工作利润为0也没问题
我们要的是这两种情况的和，毕竟我们求的是种类
注意我们每一次求完这两个状态后要取模1e9+7

再来看我们初始化，我们仅需处理i==0情况，即没有工作时候，其他都已经特判过了不会使用到

若i==0且k>0时，dp[0][j][k] = 0 ，因为没有工作，不可能产生≥k（k>0）的利润，因此方案数为0

此时如果i == 0 && k == 0，表示没有工作也没有利润，此时我们依然可以选一种，因为空集也是一种选法，这样我们选了也没有利润，即dp[0][j][0] = 1 (0<=j<=n)

我们保证i从小到大（工作从前往后选）填表，最后返回dp[原始数组长度][n][m]

java 复制代码

class Solution {
    public int profitableSchemes(int n, int minProfit, int[] group, int[] profit) {
        //这道题说人话就是从所有计划中挑几个计划，让其构成的子集中利润至少为minProfit，人数不能超过n
        //定义dp[i][j][k]表示从前i个计划中调出几个计划，让其总人数不超过j个人，利润至少为k，所有可能的选法
        int length = group.length;
        int [][][] dp = new int[length+1][n+1][minProfit+1];
        //初始化，当没有计划的时候，我们利润也是0，只有一种选法，即空集选法，这时候无论你多少个人都没用
        for(int i = 0;i <= n;i++){
            dp[0][i][0] = 1;
        }
        //填表
        for(int i = 1;i <= length;i++){
            for(int j = 0;j <= n;j++){
                for(int k = 0;k <= minProfit;k++){
                    dp[i][j][k] = dp[i-1][j][k];
                    //我们要保证这个计划的需求人数不能超过我们此时的人数
                    //注意我们的利润不作要求，即使当前计划利润很大，我们也是要接受的，利润越多越好
                    //但是为了避免k-p[i]越界，因此当k-p[i]<0时候，我们认为当前计划利润更大，此时k-p[i]=0
                    if(group[i-1] <= j){
                        dp[i][j][k] += dp[i-1][j-group[i-1]][Math.max(0,k-profit[i-1])];
                    }
                    //记得要取模
                    dp[i][j][k] %= (int)1e9+7;
                }
            }
        }
        return dp[length][n][minProfit];
    }
}

空间优化版

java 复制代码

class Solution {
    public int profitableSchemes(int n, int minProfit, int[] group, int[] profit) {
        //这道题说人话就是从所有计划中挑几个计划，让其构成的子集中利润至少为minProfit，人数不能超过n
        //定义dp[i][j][k]表示从前i个计划中调出几个计划，让其总人数不超过j个人，利润至少为k，所有可能的选法
        int length = group.length;
        int [][] dp = new int[n+1][minProfit+1];
        //初始化，当没有计划的时候，我们利润也是0，只有一种选法，即空集选法，这时候无论你多少个人都没用
        for(int i = 0;i <= n;i++){
            dp[i][0] = 1;
        }
        //填表
        for(int i = 1;i <= length;i++){
            for(int j = n;j >= group[i-1];j--){
                for(int k = minProfit;k >= 0;k--){
                    //我们要保证这个计划的需求人数不能超过我们此时的人数
                    //注意我们的利润不作要求，即使当前计划利润很大，我们也是要接受的，利润越多越好
                    //但是为了避免k-p[i]越界，因此当k-p[i]<0时候，我们认为当前计划利润更大，此时k-p[i]=0
                        dp[j][k] += dp[j-group[i-1]][Math.max(0,k-profit[i-1])];
                    //记得要取模
                    dp[j][k] %= (int)1e9+7;
                }
            }
        }
        return dp[n][minProfit];
    }
}

三、看起来是背包其实不是---组合总数IV

题目链接

这一题你看题目乍看，每个数可以重复使用，还有一个目标和，你觉得是一个完全背包

但是你仔细看题目发现，并不是求的组合个数，而是求的排列个数，因为我们发现
nums[1,2,3] target=4，此时有这几种情况1+1+2=4,1+2+1=4,2+1+1=4，如果是组合，因为数字都是无序的，因此这三种情况本质是相同选法，但是题目中说是三种不同选法，则说明这每个数字是有序的

我们背包问题解决的是无序的情况，本质上求的是组合个数，因为我们背包问题求的是所有选择方法，其内部并未按照规定要求排序

换句话来说，背包问题对于每个物品，我们是 "批量" 处理它的所有选择次数，不会出现 "先选 A 再选 B" 和 "先选 B 再选 A" 的两种顺序

因此这一题就按照常规的动态规划方法去做，这一题我们根据其重复子问题抽象出状态表示
dp[i]表示凑成总和为i一共有多少种排列个数

因此我们来推导状态转移方程

我们求的是有多少种排列，那我们要想让这个排列凑成i，那么我们要去看看凑成i-数组中的值有多少种排列，我们当前i位置元素再添加到这个数组中值末尾就好

但是要保证，i >= 数组中值，因为如果数组中值很大，本身就已经超过了i，此时i-这个数字中值 = 负数，但是我们题目数组中值都是>0的

我们再来看初始化方面，dp[0]表示凑成0有多少种方案，我们只需要选一个空集就好，同时也可以理解为为后续填表正确，因此dp[0] = 1

我们从左往右填表，最后返回dp[target]就好

java 复制代码

class Solution {
    public int combinationSum4(int[] nums, int target) {
        //这道题就是有误导人的地方，说是组合个数，其实是排列个数（顺序有关）
        //dp[i]表示凑成i一共有多少种排列数
        int [] dp = new int[target+1];
        //为了保证好后续填表正确，并且凑成0仅仅需要选一个空集就好
        dp[0] = 1;
        for(int i = 1;i <= target;i++){
            //枚举所有的数
            for(int num : nums){
                //要保证这个数字要比我们想要凑出的数字小，不然凑不出来
                if(num <= i){
                    dp[i] += dp[i-num];
                }
            }
        }
        return dp[target];
    }
}

四、卡特兰数------不同的二叉搜索树

题目链接

这一题我们通过抽象发现了重复子问题
dp[i]表示节点个数为i的时候一共有多少种二叉搜索树

因此我们这样推导状态转移方程，假设有1~i这些数，我们任意悬疑个数j作为根节点，此时左子树有j-1个节点，右子树有i-j-1+1个节点

因此我们统计左右子树有多少个二叉搜索树就好，此时左右子树再互相组合，因此就为dp[i] += dp[j-1]*dp[i-j]

为什么是*，因为左右子树可以任意互相组合，就是在求笛卡尔积

对于初始化，dp[0]表示初始是空树，空树也是一种二叉搜索树，dp[0] = 1

我们从左往右填表，最后返回dp[n]

java 复制代码

class Solution {
    public int numTrees(int n) {
        //dp[i]表示以节点个数为i个的时候有多少种二叉搜索树
        int [] dp = new int[n+1];
        //初始化，空树也是一种二叉搜索树
        dp[0] = 1;
        //填表，枚举节点个数
        for(int i = 1;i <= n;i++){
            //枚举每一个节点为根节点情况
            for(int j = 1;j <= i;j++){
                dp[i] += dp[j-1]*dp[i-j];
            }
        }
        return dp[n];
    }
}

感谢你的阅读，祝你每道题都完美AC

动态规划系列到此结束了QAQ

END

硅基计划4.0 算法 动态规划高阶

文章目录

一、双数组DP

1. 最长公共子序列

2. 不相交的线

3. 不同的子序列

4. 通配符匹配

5. 正则表达式匹配

6. 交错字符串

7. 两个字符串最小ASCII删除和

8. 最长重复子数组

二、背包问题

I. 01背包问题

1. 模板题

2. 分割等和子集

3. 目标和

4. 最后一块石头重量II

II. 完全背包

1. 模板题

2. 零钱兑换

3. 零钱兑换II

4. 完全平方数

III. 二维费用的背包问题

1. 一和零

2. 盈利计划

三、看起来是背包其实不是---组合总数IV

四、卡特兰数------不同的二叉搜索树

硅基计划4.0 算法动态规划高阶