

💗博主介绍:计算机专业的一枚大学生 来自重庆 @燃于AC之乐✌专注于C++技术栈,算法,竞赛领域,技术学习和项目实战✌💗
💗根据博主的学习进度更新(可能不及时)
💗后续更新主要内容:C语言,数据结构,C++、linux(系统编程和网络编程)、MySQL、Redis、QT、Python、Git、爬虫、数据可视化、小程序、AI大模型接入,C++实战项目与学习分享。
👇🏻 精彩专栏 推荐订阅👇🏻
🌟算法相关题目点击即可进入实操🌟
感兴趣的可以先收藏起来,请多多支持,还有大家有相关问题都可以给我留言咨询,希望希望共同交流心得,一起进步,你我陪伴,学习路上不孤单!
文章目录
前言
这些题目摘录于洛谷,好题,典型的题,考察各类算法运用,可用于蓝桥杯及各类算法比赛备战,算法题目练习,提高算法能力,补充知识,提升思维。
锻炼解题思路,从学会算法模板后,会分析,用到具体的题目上。
对应题目点链接即可做。
本期涉及算法:动态规划--多重背包,贪心 + 差分,贪心算法,dfs暴搜,数学(解决应用题),动态规划--路径dp(方格取数问题)。
题目清单
1.Tallest Cow S (最高的奶牛)

题目: P2879 [USACO07JAN] Tallest Cow S


解法:贪心 + 差分
题目要求右端点大于等于左端点,且中间更小,满足要求的最大安排,我们开始可以贪心地构造,开始让所有的奶牛一样最高(因为最高值这里给出了),左可以等于右,中间的小于两边的端点,让中间的只少1,那么就是每给一段区间,让中间的区间全部-1,想到用差分数组进行处理。最后的值:起始最高的高度 + 前缀和处理后的差分数组对应值(处理后的变化量)。
特殊处理:1.这道题会有重复数据 ,不用再处理,因为此时以满足要求,要最高,每处理一次高度会减小,要用set<pair<int, int>> mp ; 来存,帮助去重 ,同时可以用mp.count({a, b})标记当前数据是否存过 ,结束,优化; 2.a > b, 要swap(a, b)。
代码:
cpp
#include <iostream>
#include <set>
using namespace std;
const int N = 1e4 + 10;
int n, id, h, r;
int f[N]; //差分数组
int main()
{
cin >> n >> id >> h >> r;
set<pair<int, int>> mp; //会有重复的修改区间,去重
while(r--)
{
int a, b; cin >> a >> b;
if(a > b) swap(a, b);
//[a + 1, b - 1]
if(mp.count({a, b})) continue; //重复的不再进行修改
f[a + 1]--;
f[b]++;
mp.insert({a, b});
}
for(int i = 1; i <= n; i++)
{
f[i] += f[i - 1];
cout << h + f[i] << endl; //开始默认都为最大高度h,然后按题目输入条件修改, h + 变化量
}
return 0;
}2.英雄联盟


解法:动态规划--多重背包
从前往后挑选皮肤(物品),搭配的展示方案数 >= M的最小花费,且物品数有限制,可以想到多重背包问题。
1.状态表示:
这道题的精彩之处,可以有两种状态表示,其中一种不行。
这里有两种状态表示都能解决问题:
a. f[i] [j] 表示从前 i 个英雄中挑选,总⽅案数不低于 j 时,此时的最小花费;
b. f[i] [j] 表示从前 i 个英雄中挑选,总花费为 j 时,此时的最大方案数。
如果选第⼀种,时间和空间都会超,因为第⼆维的最大值是1e17 。因此,我们选择第⼆种状态
表示。在打表结束之后,从前往后扫描最后一行,从f[n] [1] 开始找出第⼀个方案数超过m的花费为最小,即为结果。
2.状态转移方程:
根据第i个英雄选择皮肤数量分类讨论,假设选了p 个皮肤,其中0 <= p <=k[i] ,并且 p * c[i] <= j , 此时的最大方案数为f[i - 1] [j - p * c[i]] * p 。也就是前i - 1个英雄中挑选,总价值为**j - p * c[i]**时最大方案数再乘上此时的选择数量。
因为要的是最大值,所以状态转移⽅程就是所有合法 k 情况下的最⼤值。
3.初始化:
f[0] [0] = 1 ,因为后续方案数是累乘,所以这⾥初始化为 1 就能保证后续
填表是正确的。
代码:
cpp
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 300, M = 1e6 + 10;
LL n, m;
LL cnt[N], v[N];
LL f[M];
LL sum; //最大花费
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> cnt[i];
for(int i = 1; i <= n; i++)
{
cin >> v[i];
sum += v[i] * cnt[i];
}
f[0] = 1;
for(int i = 1; i <= n; i++)
{
for(int j = sum; j >= 0; j--)
{
for(int k = 0; k <= cnt[i] && k * v[i] <= j; k++)
{
f[j] = max(f[j], f[j - k * v[i]] * k);
}
}
}
for(int j = 1; j <= sum; j++)
{ //从花费最小的开始找第一个满足要求的
if(f[j] > m)
{
cout << j << endl;
break;
}
}
return 0;
}3.小A的糖果
题目: P3817 小A的糖果

解法:贪心
从前往后考虑每个盒子糖果数,如果第i个盒子,a[i] + a[i - 1] > x, 拿走糖果。
怎么拿?
贪心1: 想到拿尽量少 且满足要求,即为d = a[i] + a[i - 1] -x。拿前面一个会对与后面的数量和产生影响;
贪心2: 从第二个开始 ,把开始前面一个看成0个处理 ,因为如果只有三个 2 2 2,要求不超过3,拿掉中间2一个即可。 从头开始看前一个与当前这个i的和可以合理更新。为了让后⾯相邻元素累加尽可能小,应该从 i 位置拿⾛ d 的糖果,此时 a[i] =a[i] - d ,化简完之后为 a[i] = x - a[i - 1] 。
代码:
cpp
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
LL n, x;
LL a[N];
int main()
{
cin >> n >> x;
LL sum = 0;
for(int i = 1; i <= n; i++)
{
cin >> a[i];
LL d = a[i] + a[i - 1] - x;
if(d > 0)
{
sum += d;
a[i] = x - a[i - 1];
}
}
cout << sum << endl;
return 0;
}4.Cow Picnic S(奶牛野餐)
题目: P2853 [USACO06DEC] Cow Picnic S
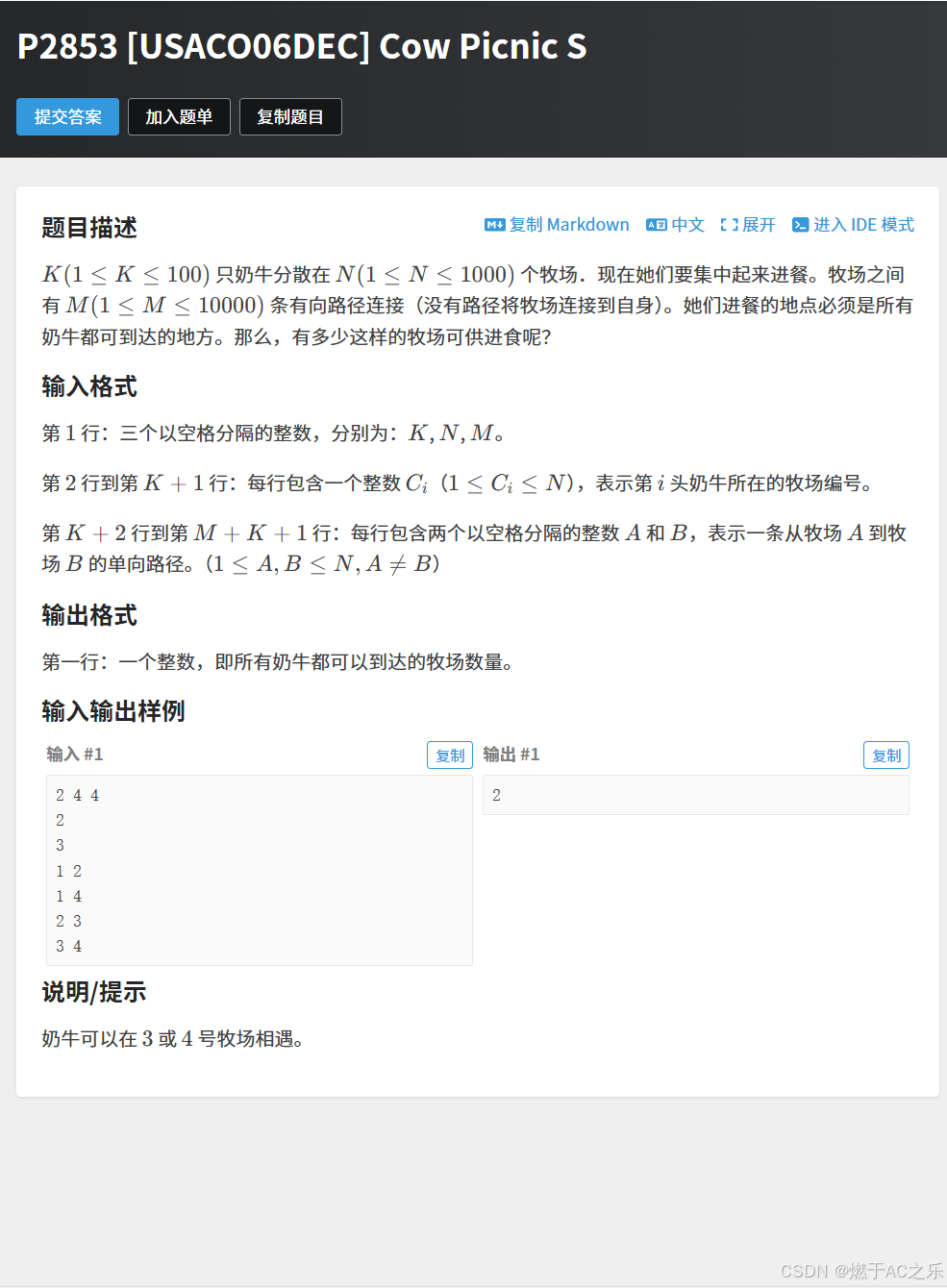
解法:dfs/bfs暴搜
要想每个奶牛都能到达牧场 ,以(k个奶牛)每个奶牛的位置为起点 做一次dfs/bfs ,标记可以到达的点,哪些结点被标记了k次,即为所求结果。
代码:
cpp
#include <iostream>
#include <cstring>
#include <vector>
using namespace std;
const int N = 1010;
int k, n, m;
int a[N]; //k头奶牛的编号
vector<int> edges[N];
int cnt[N];
bool st[N];
void dfs(int u)
{
st[u] = true;
cnt[u]++;
for(int v : edges[u])
{
if(!st[v]) dfs(v);
}
}
int main()
{
cin >> k >> n >> m;
for(int i = 1; i <= k; i++) cin >> a[i];
for(int i = 1; i <= m; i++)
{
int x, y; cin >> x >> y;
edges[x].push_back(y);
}
for(int i = 1; i <= k; i++)
{
memset(st, 0, sizeof st); //重置更新为0
dfs(a[i]);
}
int ret = 0;
for(int i = 1; i <= n; i++)
{
if(cnt[i] == k) ret++;
}
cout << ret << endl;
return 0;
}5.税收与补贴问题

题目: P1023 [NOIP 2000 普及组] 税收与补贴问题

解法:数学
设政府干预x元。
可列式子:
d = (130 - 120) / (30 - 28) = 5。
(28 - 28 + x)* 130
(29 - 28 + x)* 125,
(30 - 28 + x)* 120
(31 - 28 + x) 110*
d = 15。
(32 - 28 + x) * 95
(33 - 28 + x) * 80
......
(38 - 28 + x ) * 5
(31 - 28 + x) * 110 > =(28 - 28 + x)* 130, (29 - 28 + x)* 125, (30 - 28 + x)* 120
分别化为 x <= p1, x <= p2, x <= p3.要想全部都满足,则:
x <= (p1, p2, p3)min
(31 - 28 + x) * 110 >= (32 - 28 + x) * 95, (33 - 28 + x) * 80......(38 - 28 + x ) * 5
分别化为 x >= p4, x >= p5, x >= p6......要想全部都满足,则:
x >= (p3, p4, p5 ......)max
政府规定价格aim,成本:a,销量:c[i],表示售价为i时的对应销量。
(aim - a + x) * c[aim] >= (i - a + x) * c[i],
(aim - a) * c[aim] + x * c[aim] >= (i - a) + c[i] + x * c[i]
x * (c[aim] _ c[i]) >= (i - a) * c[i] - (aim - a) * c[aim]
1.c[aim] > c[i] , x >= ((i - a) * c[i] - (aim - a) * c[aim]) / (c[aim] _ c[i])
2.c[aim] < c[i] , x <= ((i - a) * c[i] - (aim - a) * c[aim]) / (c[aim] _ c[i])
细节处理:
left < x < right。
1.left > right,x无解;
2.right < 0, left < 0,x取绝对值较小,值较大的,就是舍 (向下取整),用floor(right);
3.right > 0, left > 0,x取绝对值较小,值较小的,就是入 (向上取整),用ceil(left);
4.left < 0, right >0,x取绝对值较小,取0。
代码:
cpp
#include <iostream>
#include <cmath>
using namespace std;
const int N = 1e5 + 10;
int aim, a;
int c[N]; //售价为 i 时,销量为 c[i]
int main()
{
cin >> aim;
int x, y; cin >> x >> y;
a = x; c[x] = y;
int prev = x; //存前一个的定价
while(cin >> x >> y, x != -1 && y != -1)
{
int d = (c[prev] - y) / (x - prev);
for(int i = prev + 1, j = c[prev] - d; i <= x; i++, j -= d)
{
c[i] = j;
}
prev = x; //还原
}
int d; cin >> d;
for(int i = prev + 1, j = c[prev] - d; j >= 0; i++, j -= d)
{
c[i] = j;
prev = i;
}
double left = -1e9, right = 1e9;
for(int i = a; i <= prev; i++)
{
double x = 1.0 * ((i - a) * c[i] - (aim - a) * c[aim]) / (c[aim] - c[i]);
if(c[aim] > c[i]) left = max(left, x);
else if(c[aim] < c[i]) right = min(right, x);
}
if(left > right) cout << "NO SOLUTION" << endl;
else if(right < 0) cout << (int)floor(right) << endl;
else if(right > 0) cout << (int)ceil(left) << endl;
else cout << 0 << endl;
return 0;
}6. 传纸条

解法:动态规划--路径类dp
类似方格取数,但与方格取数的不同点在于处理相遇点的策略,这里不能有相遇点。
1.状态表示:
f [st] [i1] [i2] 表示:第⼀条路在 [i1 , st − i1 ] ,第⼆条路在 [i2 , st − i2] 时,两者的路径最⼤和。
那我们的最终结果就是 f[n + m] [m] [m]。
2.状态转移方程:
第⼀条路可以从上[i1 - 1, st - i1]或者左[i1, st - i1 - 1]走到[i1, st - i1]位置;第⼆条路可以从上[i2 - 1, st - i2] 或者左[i2, st - i2 -1]走到[i2, st - i2] 位置。排列组合⼀下⼀共种情况,分别是:
1.上 + 上,此时的最⼤和为: f[st - 1] [i1 - 1] [i2 - 1] ;
上 + 左,此时的最⼤和为:f[st - 1] [i1 -1] [i2];
左 + 上,此时的最⼤和为:f[st - 1] [i1] [i2 - 1] ;
左 + 左,此时的最⼤和为:f[st - 1] [i1] [i2] ;
取上面四种情况的最大值,然后再加上a[i1] [j1] 和 a[i2] [j2]。
但是要注意,如果两个路径当前在同⼀位置时,直接continue,因为两条路不能走在相同的位
置。不过,如果是最后⼀个格子的话,还是要计算的。
3.初始化: 算的是路径和, 0 不会影响最终结果,直接填表。
4.填表顺序: 先从小到大循环横纵坐标之和,然后依次从小到大循环两者的横坐标。
代码:
cpp
#include <iostream>
using namespace std;
const int N = 55;
int m, n;
int a[N][N];
int f[N + N][N][N];
int main()
{
cin >> m >> n;
for(int i = 1; i <= m; i++)
for(int j = 1; j <= n; j++)
cin >> a[i][j];
for(int s = 2; s <= n + m; s++)
{
for(int i1 = 1; i1 <= m; i1++)
{
for(int i2 = 1; i2 <= m; i2++)
{
if(i1 == i2 && s != n + m) continue;
int j1 = s - i1, j2 = s - i2;
if(j1 < 1 || j1 > n || j2 < 1 ||j2 > n) continue;
f[s][i1][i2] = max(f[s][i1][i2], f[s - 1][i1 - 1][i2 - 1]);
f[s][i1][i2] = max(f[s][i1][i2], f[s - 1][i1 - 1][i2]);
f[s][i1][i2] = max(f[s][i1][i2], f[s - 1][i1][i2 - 1]);
f[s][i1][i2] = max(f[s][i1][i2], f[s - 1][i1][i2]);
f[s][i1][i2] += a[i1][j1] + a[i2][j2];
}
}
}
cout << f[n + m][m][m] << endl;
return 0;
}

加油!志同道合的人会看到同一片风景。
看到这里请点个赞 ,关注 ,如果觉得有用就收藏一下吧。后续还会持续更新的。 创作不易,还请多多支持!