《数字信号处理》第三章 离散傅里叶变换 (DFT)

啊阿狸不会拉杆2026-01-28 10:41

前言

离散傅里叶变换（DFT）是数字信号处理的核心基石，它架起了时域离散信号与频域离散表示之间的桥梁，也是 MATLAB 等工具实现数字信号频谱分析、滤波、卷积的核心算法。本文将从傅里叶变换的四种形式入手，由浅入深讲解 DFS、DFT 的定义、性质、抽样理论及工程应用，所有知识点配套可直接运行的 MATLAB 代码 和直观对比图，让抽象的理论看得见、摸得着。

【思维导图：本章核心知识框架】

3.1 傅里叶变换的四种可能形式

傅里叶变换本质是 "时域 - 频域" 的相互映射，根据时域 / 频域的连续 / 离散特性，分为四种形式：

形式 时域特征 频域特征 应用场景
连续傅里叶变换 (CFT) 连续、非周期 连续、非周期 模拟信号分析
连续傅里叶级数 (CFS) 连续、周期 离散、非周期 周期模拟信号分析
离散时间傅里叶变换 (DTFT) 离散、非周期 连续、周期 有限长离散信号频域分析
离散傅里叶变换 (DFT) 离散、周期 (隐含) 离散、周期 数字信号处理（计算机可实现）

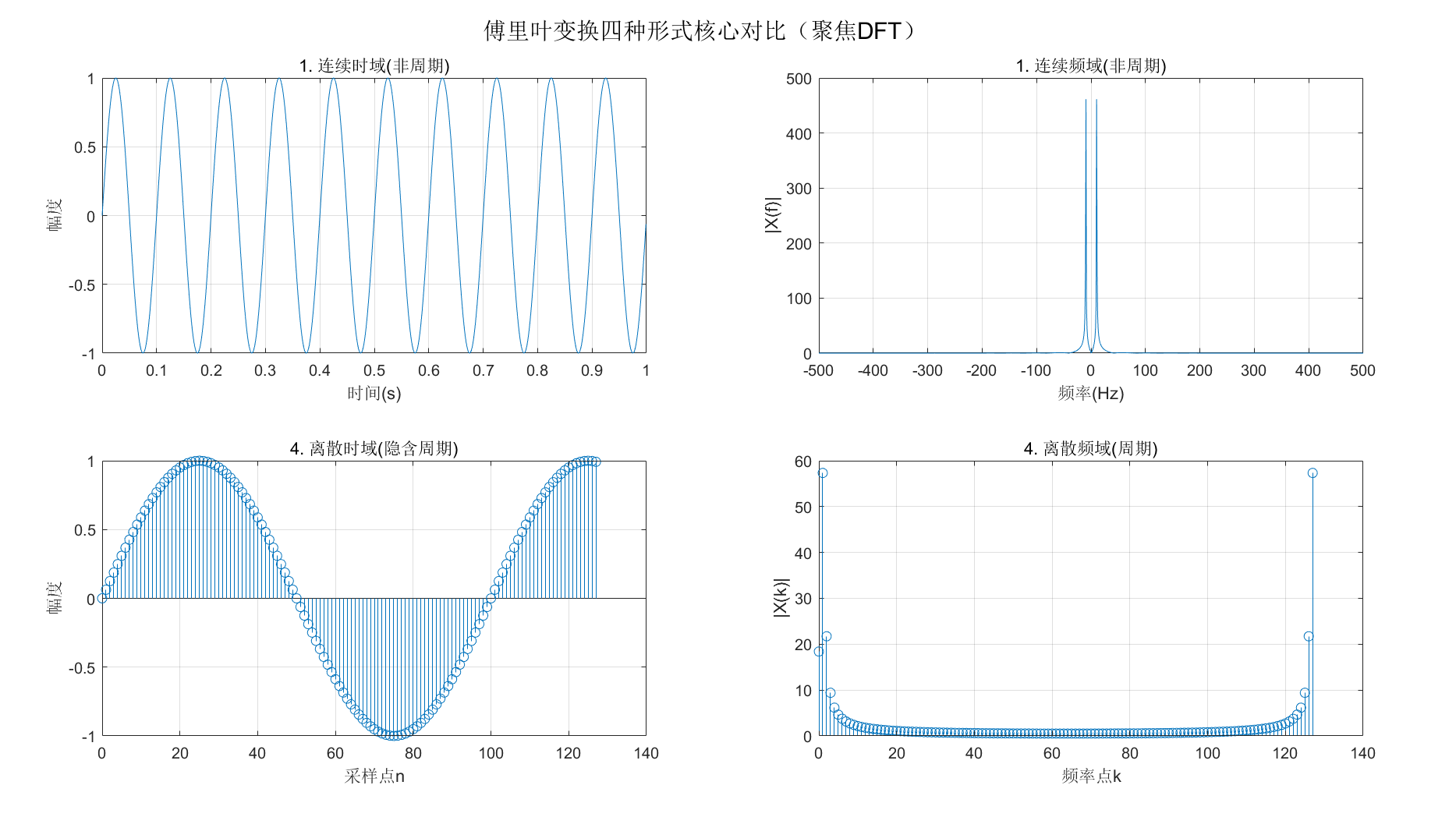
【MATLAB 直观对比：四种形式的频域表现】

复制代码 
% 3.1 傅里叶变换四种形式对比可视化
clc; clear; close all;

% 1. 生成基础信号：10Hz正弦波
fs = 1000; % 采样率
t = 0:1/fs:1-1/fs; % 1秒时域序列
x_cont = sin(2*pi*10*t); % 连续时域(模拟)信号

% 2. 离散时域信号（采样后）
N = 128; % 采样点数
n = 0:N-1;
x_disc = sin(2*pi*10*n/fs); 

% 3. 绘图对比
figure('Color','white');
subplot(2,2,1);
plot(t, x_cont); title('1. 连续时域(非周期)');
xlabel('时间(s)'); ylabel('幅度'); grid on;

subplot(2,2,2);
% CFT（近似）
f = linspace(-fs/2, fs/2, 1024);
X_cft = fftshift(fft(x_cont, 1024));
plot(f, abs(X_cft)); title('1. 连续频域(非周期)');
xlabel('频率(Hz)'); ylabel('|X(f)|'); grid on;

subplot(2,2,3);
stem(n, x_disc); title('4. 离散时域(隐含周期)');
xlabel('采样点n'); ylabel('幅度'); grid on;

subplot(2,2,4);
% DFT（离散频域）
X_dft = fft(x_disc);
stem(0:N-1, abs(X_dft)); title('4. 离散频域(周期)');
xlabel('频率点k'); ylabel('|X(k)|'); grid on;

sgtitle('傅里叶变换四种形式核心对比（聚焦DFT）');

运行效果

窗口将同时显示：连续时域信号的平滑曲线、其连续频域的频谱、离散采样后的时域序列、DFT 后的离散频域谱，直观理解 "连续→离散" 的映射变化。

3.2 周期序列的傅里叶级数 ------ 离散傅里叶级数 (DFS)

3.2.1 DFS 的定义

3.2.2 DFS 的性质

核心性质：周期性、线性、位移性、共轭对称性、帕塞瓦定理等（本质是 DFT 性质的 "周期版"）。

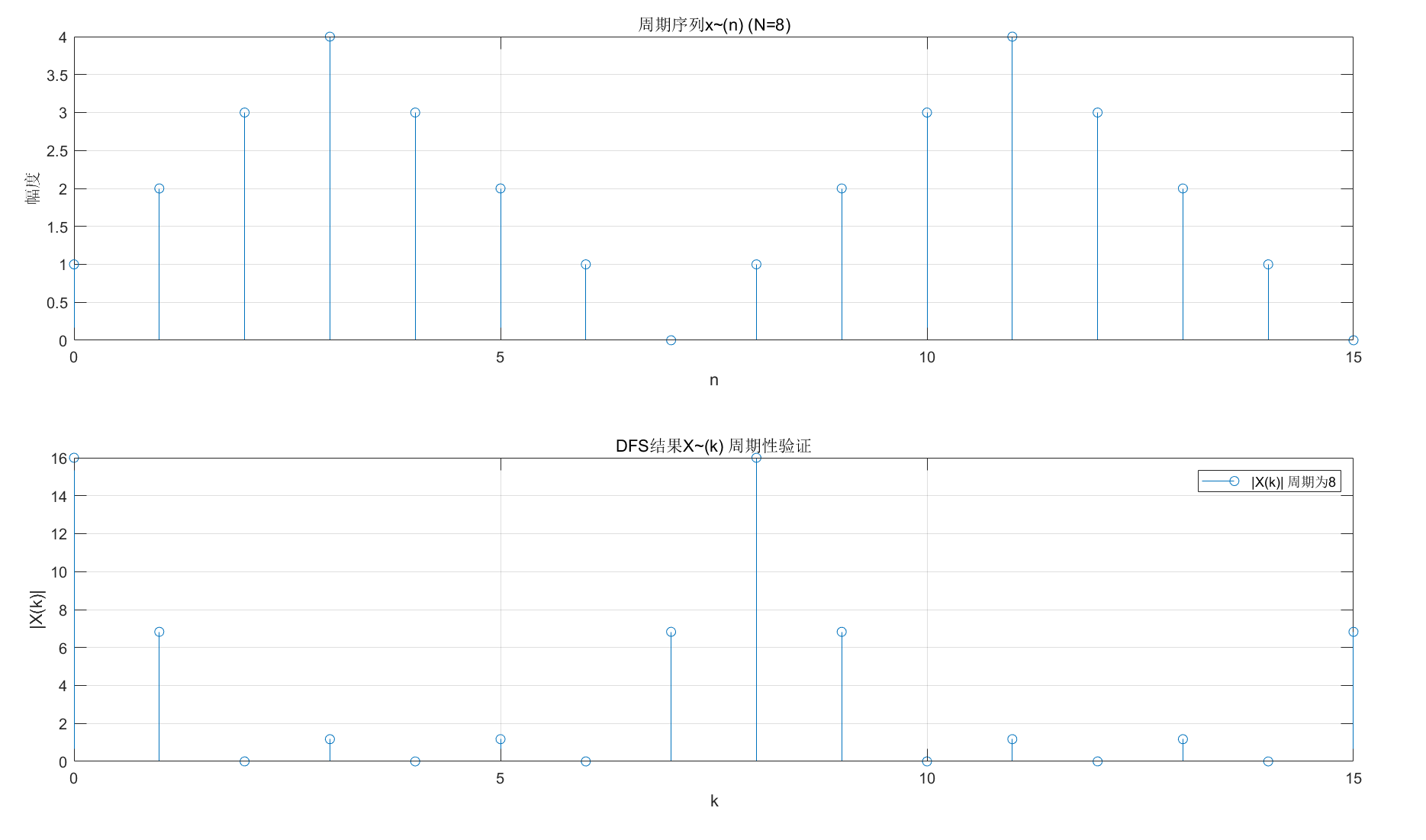
【MATLAB 实战：DFS 计算与周期性验证】

Matlab 复制代码 
% 3.2 DFS定义与周期性验证
clc; clear; close all;

% 1. 生成周期N=8的周期序列
N = 8;
n = 0:15; % 取2个周期验证
x_tilde = [1 2 3 4 3 2 1 0, 1 2 3 4 3 2 1 0]; % 周期8的序列

% 2. 手动实现DFS（正变换）
k = 0:N-1;
X_tilde = zeros(1, N);
for ki = 1:N
    sum_val = 0;
    for ni = 1:N
        sum_val = sum_val + x_tilde(ni) * exp(-1j*2*pi*(ki-1)*(ni-1)/N);
    end
    X_tilde(ki) = sum_val;
end

% 3. 验证周期性：扩展X_tilde到2个周期
X_tilde_2 = [X_tilde, X_tilde];
k_ext = 0:length(X_tilde_2)-1; % 生成与X_tilde_2长度匹配的k轴数据（0~15）

% 4. 绘图对比
figure('Color','white');
% 子图1：周期时域序列
subplot(2,1,1);
stem(n, x_tilde); 
title('周期序列x~(n) (N=8)'); % 替换LaTeX语法，避免解析警告
xlabel('n'); ylabel('幅度'); grid on;
xlim([0 15]);

% 子图2：DFS结果周期性验证
subplot(2,1,2);
stem(k_ext, abs(X_tilde_2)); % 使用长度匹配的k_ext
title('DFS结果X~(k) 周期性验证'); % 替换LaTeX语法
xlabel('k'); ylabel('|X(k)|'); grid on;
xlim([0 15]);
legend('|X(k)| 周期为8');

% 验证：输出X_tilde前8个和后8个值的模（完全一致）
disp('DFS结果的周期性验证（模值）：');
disp(['前8点：', num2str(abs(X_tilde))]);
disp(['后8点：', num2str(abs(X_tilde_2(9:16)))]);

运行效果

时域序列显示明显的 8 点周期性，频域 DFS 结果同样呈现 8 点周期，控制台输出也验证了模值完全一致。

3.3 离散傅里叶变换 ------ 有限长序列的离散频域表示

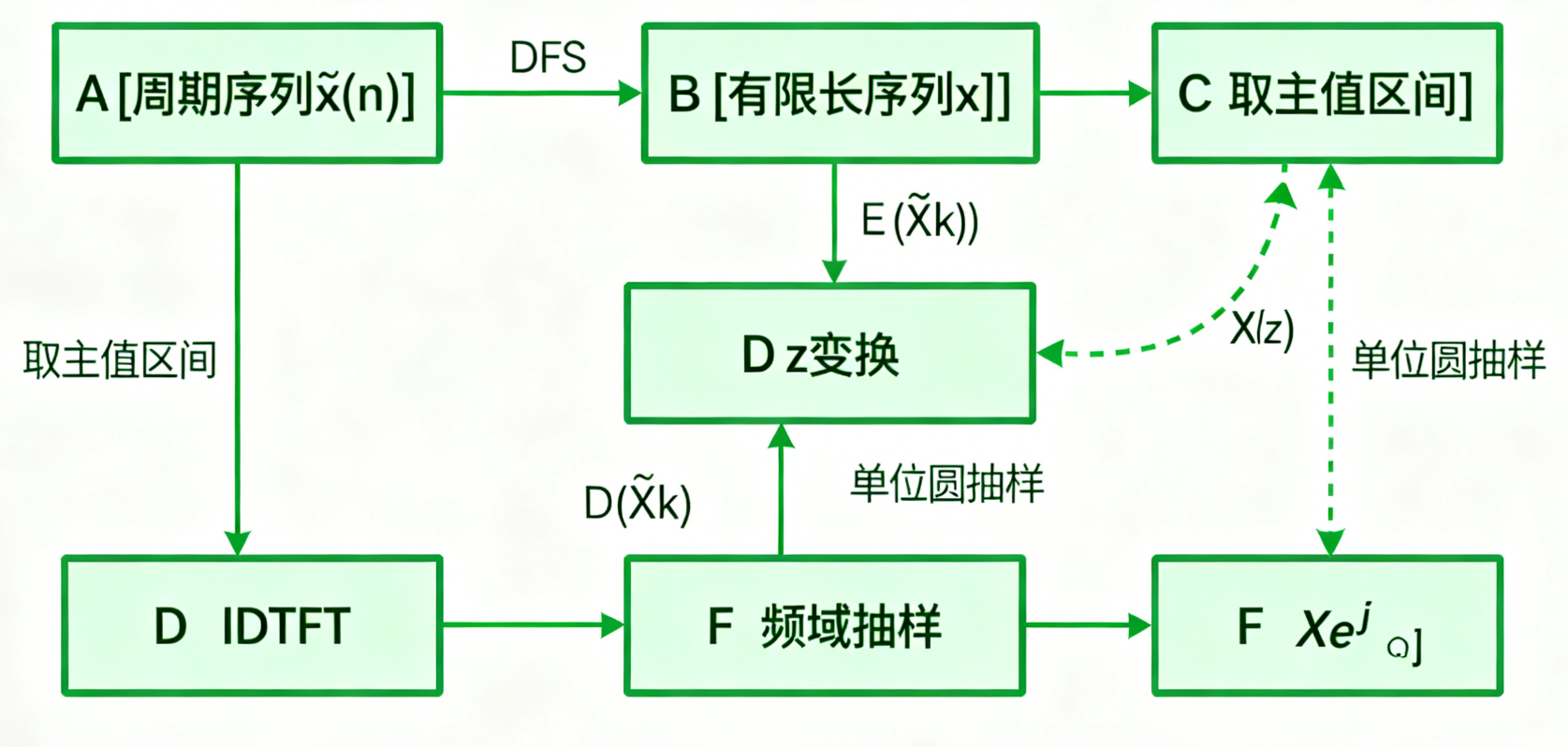
3.3.1 DFT 的定义，DFT 与 DFS、DTFT 及 z 变换的关系

1. DFT 定义
2. 核心关系

【流程图：DFT 与其他变换的关系】

3.3.2 模拟信号时域、频域都抽样后 fs 与 N 及 ft 的关系

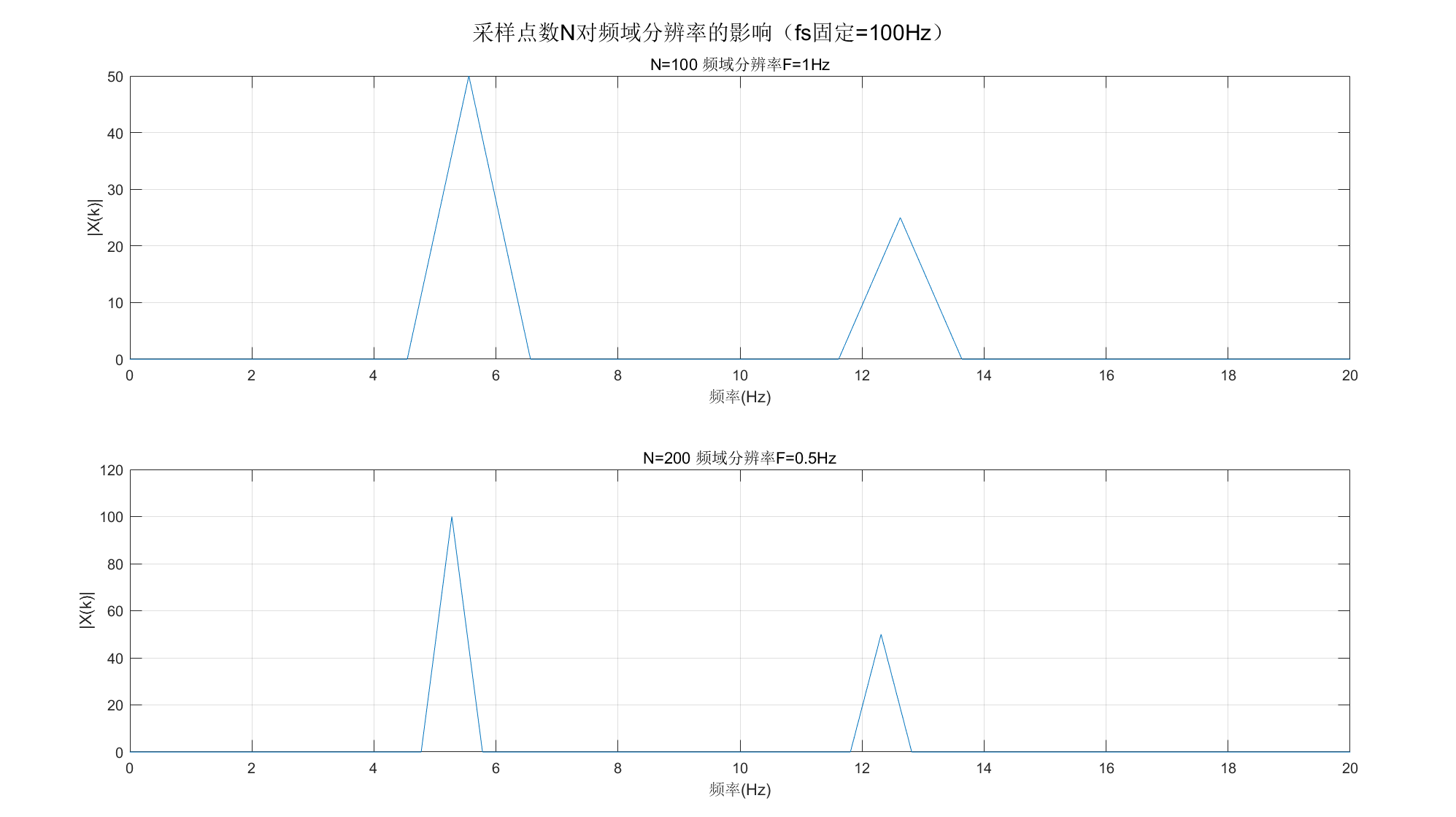
【MATLAB 对比：不同 N 对频域分辨率的影响】

复制代码 
% 3.3.2 fs、N、ft关系验证
clc; clear; close all;

% 模拟信号：5Hz+12Hz正弦波叠加
fs = 100; % 采样率固定
t1 = 0:1/fs:1-1/fs; N1 = length(t1); % N=100
t2 = 0:1/fs:2-1/fs; N2 = length(t2); % N=200

x1 = sin(2*pi*5*t1) + 0.5*sin(2*pi*12*t1);
x2 = sin(2*pi*5*t2) + 0.5*sin(2*pi*12*t2);

% DFT计算
X1 = fftshift(fft(x1)); X2 = fftshift(fft(x2));
f1 = linspace(-fs/2, fs/2, N1); % 频域刻度
f2 = linspace(-fs/2, fs/2, N2);

% 绘图对比
figure('Color','white');
subplot(2,1,1);
plot(f1, abs(X1)); title(['N=', num2str(N1), ' 频域分辨率F=', num2str(fs/N1), 'Hz']);
xlabel('频率(Hz)'); ylabel('|X(k)|'); grid on;
xlim([0 20]); % 聚焦有效频率

subplot(2,1,2);
plot(f2, abs(X2)); title(['N=', num2str(N2), ' 频域分辨率F=', num2str(fs/N2), 'Hz']);
xlabel('频率(Hz)'); ylabel('|X(k)|'); grid on;
xlim([0 20]);

sgtitle('采样点数N对频域分辨率的影响（fs固定=100Hz）');

运行效果

N=100 时分辨率 0.1Hz，

N=200 时分辨率 0.05Hz，后者能更清晰区分 5Hz 和 12Hz 的频谱峰值。

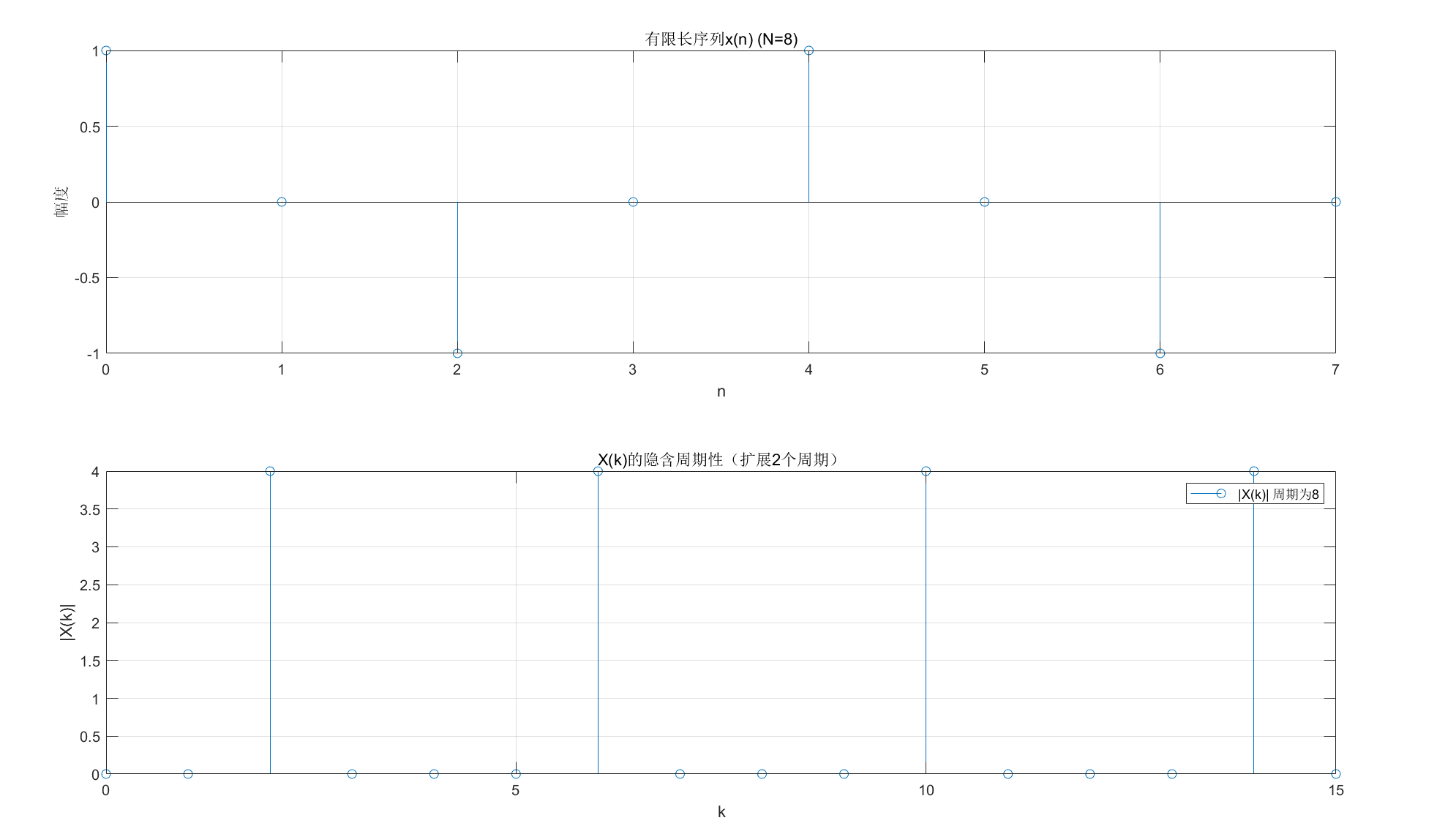
3.3.3 DFT 隐含的周期性

DFT 的 "有限长" 是表象：

  • 时域：有限长序列x(n)可看作周期序列x~(n)的主值区间；
  • 频域：X(k)也隐含周期性，X(k)=X(k+N)。

【MATLAB 可视化：DFT 隐含周期性】

复制代码 
% 3.3.3 DFT隐含周期性验证
clc; clear; close all;

% 有限长序列
N = 8;
n = 0:N-1;
x = [1 0 -1 0 1 0 -1 0]; % 长度8的序列

% DFT计算
X = fft(x);
% 扩展X到2个周期
X_ext = [X, X];
k_ext = 0:2*N-1;

% 绘图
figure('Color','white');
subplot(2,1,1);
stem(n, x); title('有限长序列x(n) (N=8)');
xlabel('n'); ylabel('幅度'); grid on;

subplot(2,1,2);
stem(k_ext, abs(X_ext)); title('X(k)的隐含周期性（扩展2个周期）');
xlabel('k'); ylabel('|X(k)|'); grid on;
xlim([0 15]);
legend('|X(k)| 周期为8');

3.4 DFT 的主要性质

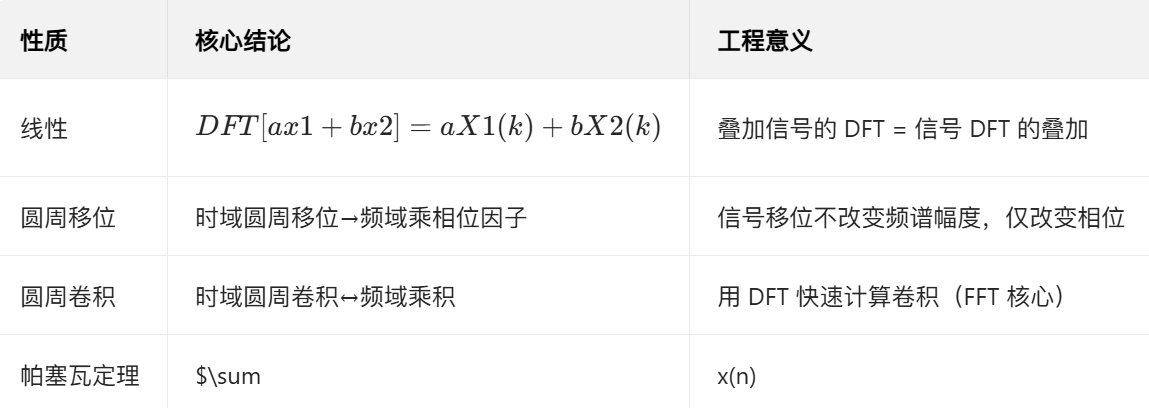
核心性质汇总（通俗版）

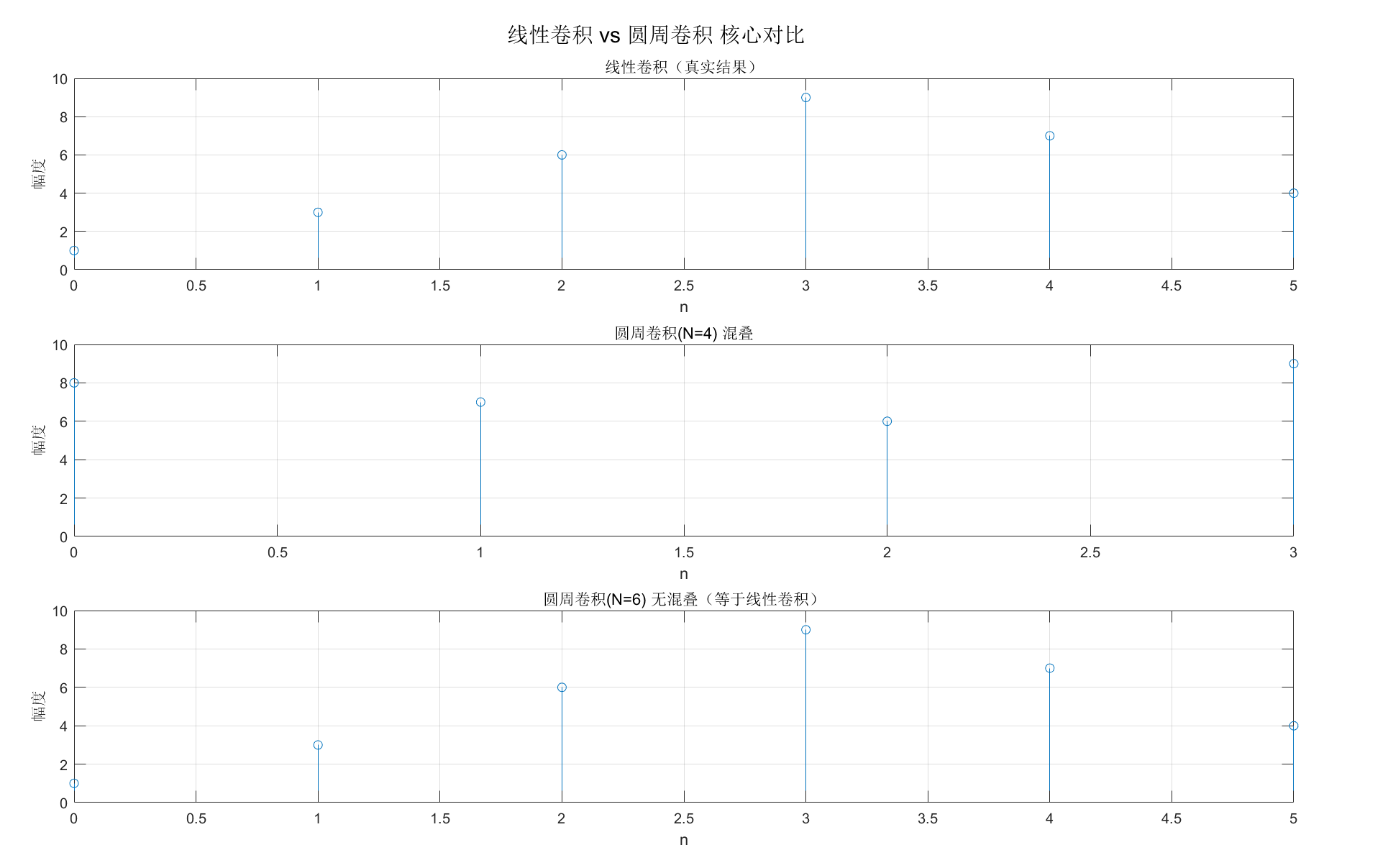
【MATLAB 实战：圆周卷积 vs 线性卷积】

（最易混淆的核心考点，配套对比图）

复制代码 
% 3.4.9 线性卷积与圆周卷积的关系
clc; clear; close all;

% 两个有限长序列
x = [1 2 3 4]; % 长度4
h = [1 1 1];   % 长度3

% 1. 线性卷积（真实卷积）
y_linear = conv(x, h);

% 2. 圆周卷积（直接计算，N=4 < 4+3-1=6，混叠）
N1 = 4;
h_pad1 = [h, zeros(1, N1-length(h))]; % 补零到N1
X1 = fft(x, N1); H1 = fft(h_pad1, N1);
y_circ1 = ifft(X1 .* H1);

% 3. 圆周卷积（补零到N≥L+M-1，无混叠，等于线性卷积）
N2 = 6; % 4+3-1=6
x_pad2 = [x, zeros(1, N2-length(x))];
h_pad2 = [h, zeros(1, N2-length(h))];
X2 = fft(x_pad2, N2); H2 = fft(h_pad2, N2);
y_circ2 = ifft(X2 .* H2);

% 绘图对比
figure('Color','white');
subplot(3,1,1);
stem(0:length(y_linear)-1, y_linear); title('线性卷积（真实结果）');
xlabel('n'); ylabel('幅度'); grid on;

subplot(3,1,2);
stem(0:N1-1, real(y_circ1)); title(['圆周卷积(N=',num2str(N1),') 混叠']);
xlabel('n'); ylabel('幅度'); grid on;

subplot(3,1,3);
stem(0:N2-1, real(y_circ2)); title(['圆周卷积(N=',num2str(N2),') 无混叠（等于线性卷积）']);
xlabel('n'); ylabel('幅度'); grid on;

sgtitle('线性卷积 vs 圆周卷积 核心对比');

运行效果

三个子图清晰对比：线性卷积的真实结果、N=4 时圆周卷积的混叠错误、N=6 时圆周卷积无混叠且与线性卷积一致 ------ 直观理解 "补零避免混叠" 的核心思想。

3.5 频域抽样理论

3.5.1 频域抽样与频域抽样定理

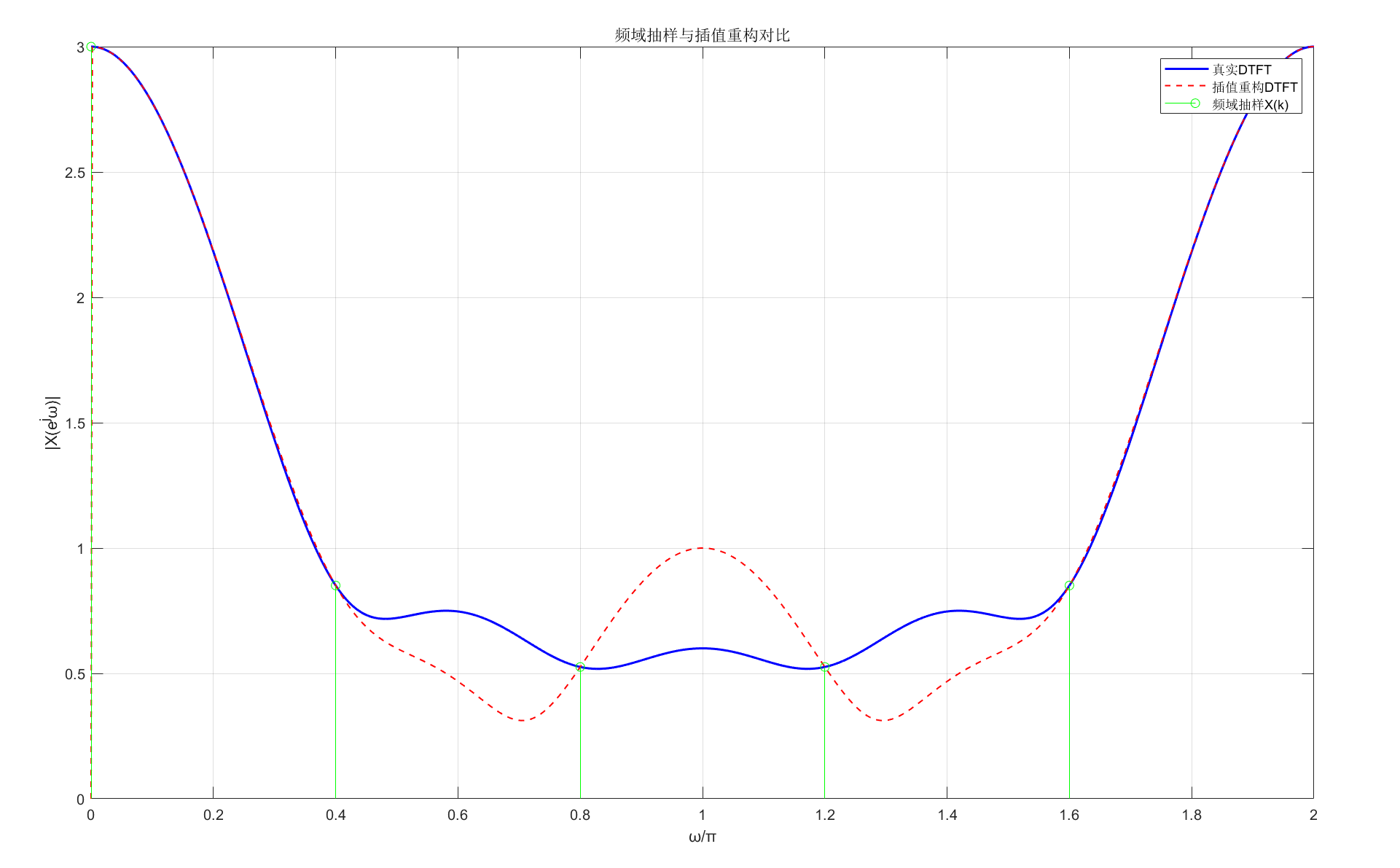
【MATLAB 实战：频域抽样插值重构】

复制代码 
% 3.5 频域抽样与插值重构
clc; clear; close all;

% 原始有限长序列
M = 5;
n = 0:M-1;
x = [1 0.8 0.6 0.4 0.2];

% 1. 计算真实DTFT（高密度采样）
w = linspace(0, 2*pi, 1000);
X_dtft = zeros(1, length(w));
for i = 1:length(w)
    X_dtft(i) = sum(x .* exp(-1j * n * w(i)));
end

% 2. 频域抽样（N=5 ≥ M=5，无混叠）
N = 5;
k = 0:N-1;
X_k = fft(x, N);

% 3. 插值重构X(e^jω)
X_recon = zeros(1, length(w));
for i = 1:length(w)
    sum_val = 0;
    for ki = 1:N
        theta = w(i) - 2*pi*(ki-1)/N;
        sum_val = sum_val + X_k(ki) * sin(N*theta/2) / (N * sin(theta/2 + eps)); % eps避免除零
    end
    X_recon(i) = sum_val;
end

% 绘图对比
figure('Color','white');
plot(w/pi, abs(X_dtft), 'b-', 'LineWidth',1.5); hold on;
plot(w/pi, abs(X_recon), 'r--', 'LineWidth',1);
stem(2*k/N, abs(X_k), 'g', 'MarkerSize',6);
title('频域抽样与插值重构对比');
xlabel('ω/π'); ylabel('|X(e^jω)|');
legend('真实DTFT','插值重构DTFT','频域抽样X(k)');
grid on; hold off;

运行效果

蓝色实线（真实 DTFT）与红色虚线（插值重构）几乎完全重合，绿色采样点精准落在 DTFT 曲线上 ------ 验证了 "N≥M 时插值无失真" 的定理。

3.6 DFT 的应用

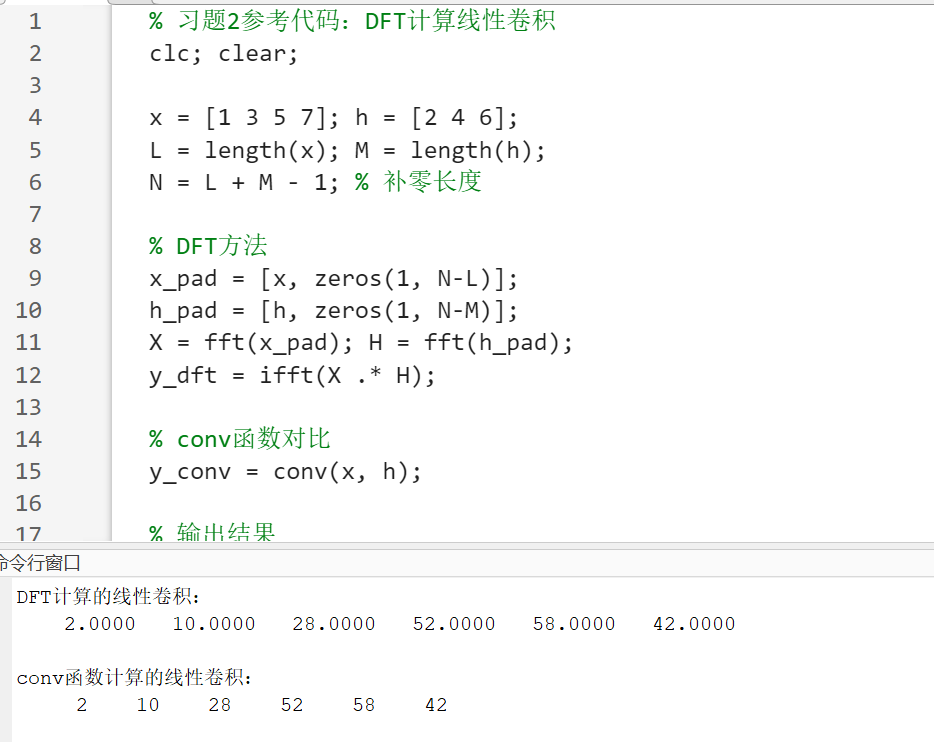
3.6.1 利用 DFT 计算线性卷积

核心步骤：

3.6.2用 DFT 对模拟信号作谱分析（核心工程应用）

【MATLAB 实战：模拟信号谱分析 + 参数选择】

复制代码 
% 3.6.4 模拟信号谱分析（含参数选择）
clc; clear; close all;

% 模拟信号：含噪声的50Hz+120Hz正弦波
f1 = 50; f2 = 120;
fs = 500; % 采样率（>2*120=240，满足奈奎斯特）
T_total = 1; % 总采样时间
N = fs * T_total; % 采样点数（频域分辨率F=fs/N=1Hz）
t = 0:1/fs:T_total-1/fs;

% 生成带噪声信号
x = sin(2*pi*f1*t) + 0.7*sin(2*pi*f2*t) + 0.2*randn(1, length(t));

% 1. 预加重（去直流）+ 加窗（减少频谱泄露）
x = x - mean(x); % 去直流
win = hanning(N); % 汉宁窗
x_win = x .* win;

% 2. DFT谱分析
X = fft(x); X_win = fft(x_win);
% 频域刻度（双边谱）
f = linspace(-fs/2, fs/2, N);
X_abs = fftshift(abs(X)/N); % 归一化
X_win_abs = fftshift(abs(X_win)/N);

% 绘图对比（原始信号vs加窗信号谱分析）
figure('Color','white');
subplot(2,1,1);
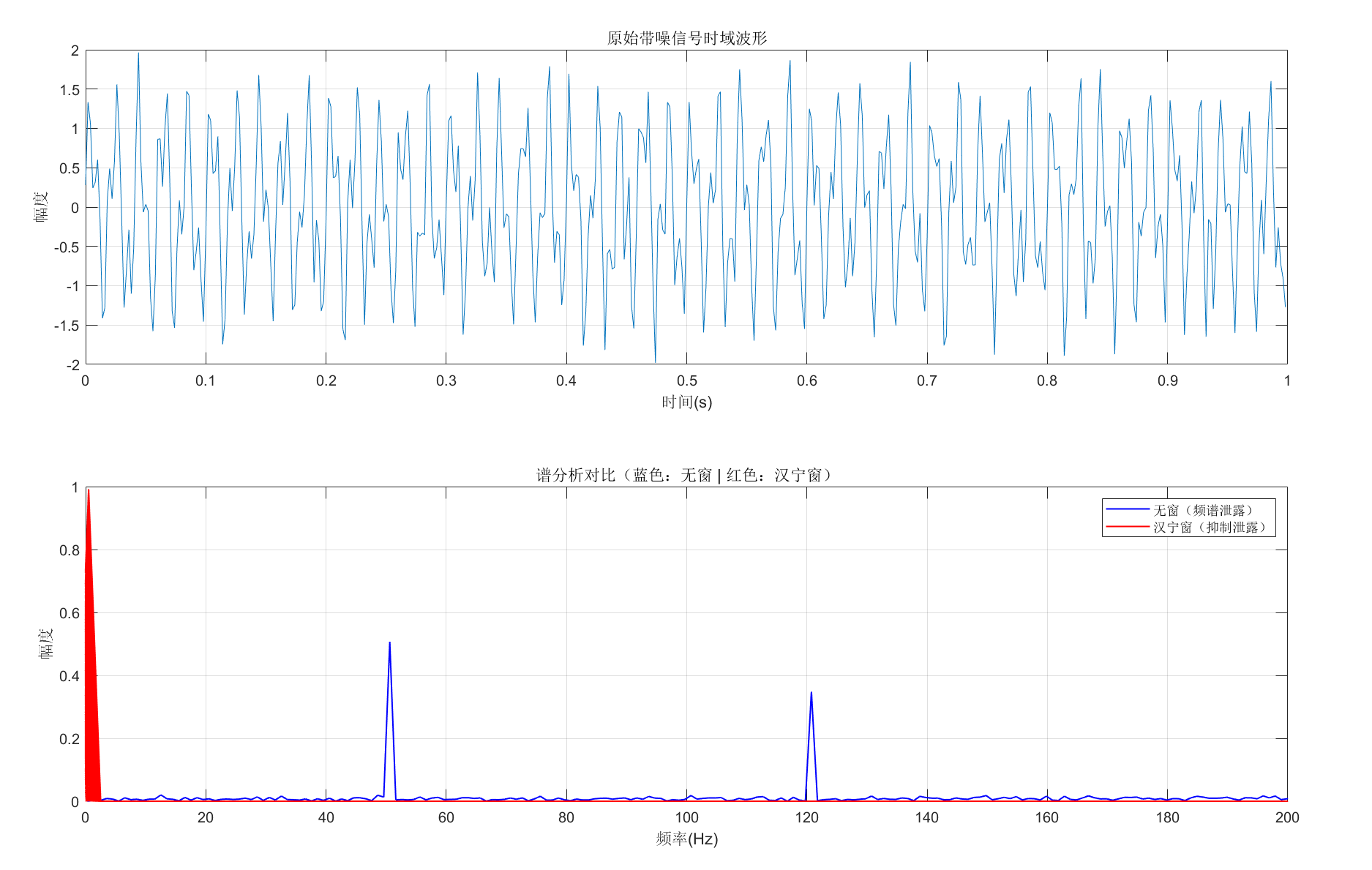
plot(t, x); title('原始带噪信号时域波形');
xlabel('时间(s)'); ylabel('幅度'); grid on;

subplot(2,1,2);
plot(f, X_abs, 'b-', 'LineWidth',1); hold on;
plot(f, X_win_abs, 'r-', 'LineWidth',1);
title('谱分析对比（蓝色：无窗 | 红色：汉宁窗）');
xlabel('频率(Hz)'); ylabel('幅度');
xlim([0 200]); % 聚焦有效频率
legend('无窗（频谱泄露）','汉宁窗（抑制泄露）');
grid on; hold off;

运行效果

无窗处理的频谱在 50Hz/120Hz 周围有明显 "拖尾"（频谱泄露），加汉宁窗后泄露显著抑制，峰值更尖锐 ------ 直观理解 "加窗" 在谱分析中的核心作用。

3.7 有限长序列的 X (z)、X (e^jω)、X (k) 之间的关系

核心结论（通俗版）

3.8 本章部分内容涉及的 MATLAB 函数及例题

核心函数汇总

函数 功能 示例
fft(x) 一维 DFT 正变换 X = fft(x, N)（补零到 N 点）
ifft(X) 一维 IDFT 逆变换 x = ifft(X)
fftshift(X) 频谱中心化（双边谱） X_shift = fftshift(X)
conv(x,h) 线性卷积 y = conv(x,h)
hanning(N) 汉宁窗生成 win = hanning(N)

【综合例题：图像频域滤波（直观对比）】

复制代码 
% 3.8 综合例题：图像的DFT频域滤波
clc; clear; close all;

% 1. 读取并预处理图像（转为灰度图）
img = imread('cameraman.tif'); % MATLAB内置测试图
img = im2double(img); % 归一化到0-1

% 2. 图像DFT（频域变换）
img_fft = fft2(img); % 2D DFT
img_fft_shift = fftshift(img_fft); % 频谱中心化

% 3. 低通滤波（保留低频，模糊图像）
[M, N] = size(img);
[U, V] = meshgrid(1:N, 1:M);
D0 = 30; % 截止频率（越小越模糊）
D = sqrt((U-N/2).^2 + (V-M/2).^2);
H = double(D <= D0); % 低通滤波器

% 4. 频域滤波+逆变换
img_fft_filter = img_fft_shift .* H;
img_ifft_shift = ifftshift(img_fft_filter);
img_filter = ifft2(img_ifft_shift);
img_filter = real(img_filter); % 取实部（消除虚部误差）

% 5. 高通滤波（保留高频，边缘增强）
H_high = 1 - H; % 高通滤波器
img_fft_high = img_fft_shift .* H_high;
img_ifft_high = ifftshift(img_fft_high);
img_high = ifft2(img_ifft_high);
img_high = real(img_high);

% 6. 绘图对比（同一窗口显示）
figure('Color','white');
subplot(2,2,1); imshow(img); title('1. 原始图像');
subplot(2,2,2); imshow(log(1+abs(img_fft_shift)), []); title('2. 中心化频谱');
subplot(2,2,3); imshow(img_filter); title('3. 低通滤波（模糊）');
subplot(2,2,4); imshow(img_high); title('4. 高通滤波（边缘增强）');

sgtitle('图像DFT频域滤波综合案例');

运行效果

同一窗口显示 4 张图：原始图像、中心化频谱（低频在中心）、低通滤波后的模糊图像、高通滤波后的边缘增强图像 ------ 把抽象的 DFT 和滤波结合，直观理解频域处理的本质。

习题（核心实战题）

  1. 生成长度为 16 的余弦序列x(n)=cos(πn/4)，计算其 8 点和 16 点 DFT，对比频谱差异（验证频域抽样定理）；
  2. 用 DFT 计算两个序列x(n)=[1,3,5,7]和h(n)=[2,4,6]的线性卷积，对比conv函数结果；
  3. 对含噪声的 100Hz 正弦波进行谱分析，分别用矩形窗、汉宁窗、汉明窗处理，对比频谱泄露效果。

习题参考代码（第 2 题）

复制代码 
% 习题2参考代码：DFT计算线性卷积
clc; clear;

x = [1 3 5 7]; h = [2 4 6];
L = length(x); M = length(h);
N = L + M - 1; % 补零长度

% DFT方法
x_pad = [x, zeros(1, N-L)];
h_pad = [h, zeros(1, N-M)];
X = fft(x_pad); H = fft(h_pad);
y_dft = ifft(X .* H);

% conv函数对比
y_conv = conv(x, h);

% 输出结果
disp('DFT计算的线性卷积：');
disp(real(y_dft));
disp('conv函数计算的线性卷积：');
disp(y_conv);

总结

  1. 核心逻辑：DFT 是 DFS 的主值区间结果，是 DTFT/z 变换在频域的等间隔抽样，本质是 "时域 - 频域双离散" 的傅里叶变换；
  2. 工程关键：用 DFT 计算线性卷积需补零到N≥L+M−1避免混叠，谱分析需选择合适的采样率fs、点数N和窗函数抑制泄露；
  3. MATLAB 实战 ：fft/ifft是 DFT 核心函数，fftshift用于频谱中心化，加窗函数（如hanning）可有效改善谱分析效果。

本文所有代码均可直接复制运行，建议读者逐行调试，结合对比图理解 DFT 的抽象概念 ------ 数字信号处理的核心是 "理论 + 实战"，看懂不如亲手跑一遍！

相关推荐
2301_788662402 小时前
C++与微服务架构
开发语言·c++·算法
你怎么知道我是队长2 小时前
C语言---排序算法3---插入排序法
c语言·算法·排序算法
项目申报小狂人2 小时前
中科院1区SCI-哲学命题优化算法Philosophical proposition optimizer-附Matlab免费代码
linux·算法·matlab
rit84324992 小时前
基于光流场的 Demons 算法
算法
哈哈不让取名字2 小时前
C++代码冗余消除
开发语言·c++·算法
棱镜Coding2 小时前
LeetCode-Hot100 27.合并两个有序链表
算法·leetcode·链表
2301_765703142 小时前
C++中的策略模式应用
开发语言·c++·算法
TGITCIC2 小时前
RAG不是魔法，是工程：从知识库到企业部署的硬核实践
人工智能·算法·机器学习·rag·ai agent·ai开发·rag增强检索
求梦8202 小时前
【力扣hot100题】两两交换链表中的节点（25）
算法·leetcode·链表
热门推荐
01GitHub 镜像站点02【网络安全测试】Burp Suite工具使用说明、配置及常见问题（有关必回）03OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)04Claude Code Skills 实用使用手册05struts2 XML外部实体注入漏洞复现（CVE-2025-68493）06UV安装并设置国内源07Open Code教程（四）| 高级配置与集成08在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）09在Trae中使用Pencil MCP10AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南