
针对无人机在三维复杂环境中的自主路径规划问题,本文选取了三种具有代表性的规划方法进行对比分析,分别为 A * 算法、快速扩展随机树(Rapidly-exploring Random Tree, RRT) 算法以及 人工势场法(Artificial Potential Field, APF) 。三种算法在搜索机理、适用场景及规划性能方面各具特点,具有较强的互补性。
完整代码压缩包解压后,直接用MATLAB运行主函数即可。
文章目录
- 程序介绍
-
- [A* 算法](#A* 算法)
- [RRT 算法](#RRT 算法)
- 人工势场法(APF)
- 综合对比分析
- 代码运行结果
- MATLAB代码
程序介绍
A* 算法
A* 算法是一种基于启发式搜索的确定性路径规划方法,通常在离散化的栅格空间中工作。该算法通过构造代价函数
f ( n ) = g ( n ) + h ( n ) f(n)=g(n)+h(n) f(n)=g(n)+h(n)
在保证搜索最优性的同时提升搜索效率,其中g(n)表示从起点到当前节点的累计代价,h(n)为当前节点到目标点的启发式估计代价。
在三维路径规划问题中,A* 算法能够在已知环境下稳定地搜索到一条全局最优或次优路径,路径质量高、可重复性强,常作为路径规划算法性能评估的基准方法。但其计算复杂度随空间维度和分辨率快速增长,对环境建模和存储资源要求较高。
RRT 算法
RRT(Rapidly-exploring Random Tree)算法是一种基于随机采样的增量式路径规划方法,主要面向高维连续空间的可行路径搜索问题。该算法通过在状态空间中随机采样,并不断向采样点方向扩展搜索树,从而快速覆盖可行空间并寻找从起点到目标点的连通路径。
在三维无人机路径规划场景下,RRT 算法具有较强的全局探索能力和环境适应性,尤其适合障碍物分布复杂或空间维度较高的情况。然而,由于其随机性特征,RRT 生成的路径通常并非最优,路径平滑性较差,规划结果在不同运行中存在一定差异。
人工势场法(APF)
人工势场法是一种基于连续空间建模的实时路径规划方法,其核心思想是将目标点视为产生吸引势场的源,将障碍物视为产生斥力势场的源,无人机在合力作用下沿势场梯度方向运动。
该方法计算结构简单、实时性强,适合对计算资源和响应速度要求较高的无人机在线规划任务。但在复杂障碍环境中,人工势场法容易陷入局部极小点,缺乏全局最优性和完备性保障,通常需要与随机扰动或全局规划方法结合使用。
综合对比分析
总体而言,A* 算法在路径最优性和稳定性方面表现突出,适合已知环境下的全局规划;RRT 算法在高维复杂空间中具有良好的可行性和扩展能力,适合快速获得可行路径;人工势场法则在计算效率和实时性方面具有优势,适用于局部路径调整与在线避障。通过在统一三维仿真环境下对三种算法进行对比,可以直观地分析不同规划策略在路径质量、计算复杂度及适用场景方面的差异,为无人机路径规划算法的选择与改进提供参考依据。
代码运行结果
规划的路径对比:
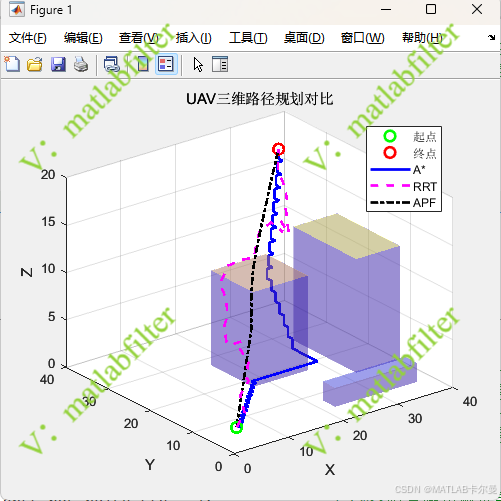
高度剖面:
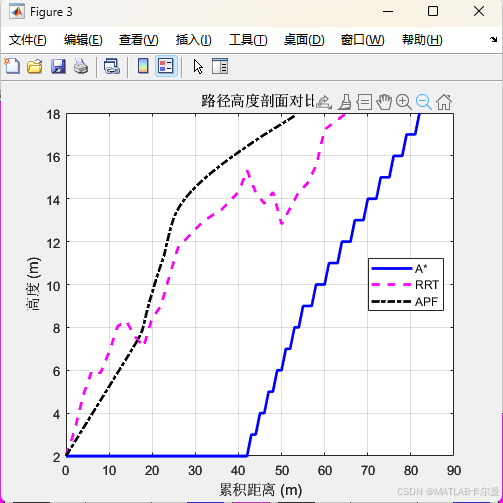
命令行截图:
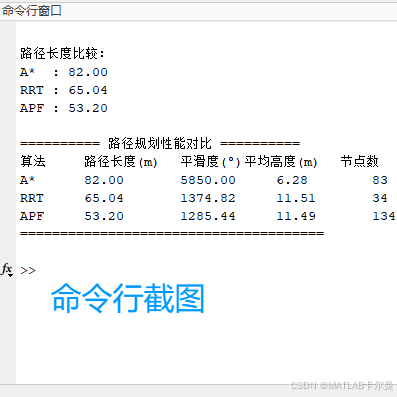
XoY投影对比:
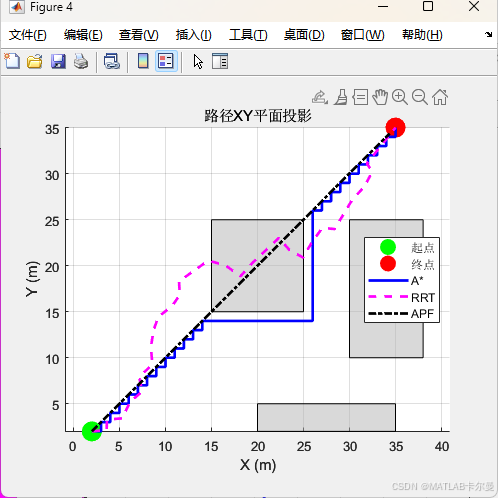
MATLAB代码
主函数:
matlab
%% 无人机三维路径规划A*, RRT, APF
% 作者:matlabfilter
% 2026-01-26/Ver1
clear; clc; close all;
rng(0);
%% ========== 环境参数 ==========
mapSize = [40, 40, 30]; % 三维空间尺寸
start = [2, 2, 2]; %起点坐标
goal = [35, 35, 18]; %终点坐标
% 障碍物位置定义 [顶点x y z,长宽高dx dy dz]
obstacles = [
15 15 1 10 10 10;
30 10 1 8 15 12;
20 2 1 15 3 2
];
%% 路径规划
%A*
[pathA, lenA] = Astar3D(start, goal, mapSize, obstacles);
%RRT
[pathR, lenR] = RRT3D(start, goal, mapSize, obstacles);
% ===APF
[pathP, lenP] = APF3D(start, goal, obstacles, mapSize);
%% ========== 统一绘图 ==========
figure; hold on; grid on;
xlabel('X'); ylabel('Y'); zlabel('Z');
title('UAV三维路径规划对比');
view(3);
% 障碍物
for i = 1:size(obstacles,1)
drawCuboid(obstacles(i,:));
end
% 起点终点
plot3(start(1),start(2),start(3),'go','MarkerSize',8,'LineWidth',2,'DisplayName','起点');
plot3(goal(1),goal(2),goal(3),'ro','MarkerSize',8,'LineWidth',2,'DisplayName','终点');
% 路径
plot3(pathA(:,1),pathA(:,2),pathA(:,3),'b-','LineWidth',2,...
'DisplayName','A*');
plot3(pathR(:,1),pathR(:,2),pathR(:,3),'m--','LineWidth',2,...
'DisplayName','RRT');
plot3(pathP(:,1),pathP(:,2),pathP(:,3),'k-.','LineWidth',2,...
'DisplayName','APF');
legend('Location','best');
% xlim([0 mapSize(1)]); ylim([0 mapSize(2)]); zlim([0 mapSize(3)]);
%% 路径长度输出
fprintf('\n路径长度比较:\n');
fprintf('A* : %.2f\n', lenA);
fprintf('RRT : %.2f\n', lenR);
fprintf('APF : %.2f\n', lenP);完整代码:
https://download.csdn.net/download/callmeup/92590826
或: