【论文阅读】多密钥低通信轮次的联邦学习安全聚合

名称	SAMK: Secure aggregation for federated learning under multiple keys with low communication rounds
期刊	IEEE Transactions on Dependable and Secure Computing
作者	Cheng Guo, Ling Li, Ximeng Liu, Kim-Kwang Raymond Choo*, Yining Liu
DOI	10.1109/TDSC.2025.3602908

SAMK: Secure aggregation for federated learning under multiple keys with low communication rounds -- 多密钥低通信轮次的联邦学习安全聚合

• TLDR
• 背景
• 预备知识
• • [BFV 加密系统](#BFV 加密系统)
  • [Paillier 加密系统](#Paillier 加密系统)
  • 多项式插值
• 实体和威胁模型
• • 威胁模型
• SAMK
• 如何实现多密钥下的客户端单独解密
• • • 建立阶段
    • 密钥生成
    • 加密
    • • 优化计算开销
    • 聚合
    • 解密
• 总结
• • 优点
  • 缺点

TLDR

本文提出了一中适用于 多密钥 环境的安全聚合联邦学习方案 SAMK，通过利用 BFV 密文的多项式结构并结合 Paillier 同态求和，实现了 单轮 、无交互 、 多密钥独立解密 且 可容忍任意客户端掉线 的聚合方案。SAMK 允许每个客户端在不参与协同解密、且无法获取他人更新的前提下独立恢复聚合结果，从而兼顾隐私性与可用性。SAMK虽然每轮只需一次交互，但是是以通信开销为代价。

背景

• 基于同态加密的安全聚合虽然可以保护隐私，但是所有客户端使用相同的密钥，在这种情况下，可能会发生内部攻击，半诚实的客户端 可能通过使用共享密钥解密其他客户端的密文来获取其模型更新；
• 当客户端使用不同密钥时，现有方案需要额外的交互，导致通信轮次的增加；
  • 当客户端掉线时，现有方案通过额外的实体间交互来协同消除掉线客户端密钥的影响，从而确保聚合过程安全且正确地完成。

预备知识

作者主要使用了多密钥 BFV 和 Paillier 同态加密，下面主要介绍一下 BFV 加密系统，Paillier 加密系统和多项式插值进行少许介绍。

BFV 加密系统

Brakerski-Fan-Vercauteren（BFV）密码系统是一种基于环上带误差学习（RLWE）的方案，支持加法和乘法同态运算。

对于 BFV，可阅读某乎文章：全同态加密方案之BFV

在BFV 中，密文空间是多项式商环 R q = Z q [ x ] / ( X N + 1 ) \mathcal{R}_q = \mathbb{Z}_q[x]/(X^N + 1) Rq=Zq[x]/(XN+1)，其中 N N N 是 2 的幂， q q q 是密文模数。明文空间是多项式商环 R t = Z t [ x ] / ( X N + 1 ) \mathcal{R}_t = \mathbb{Z}_t[x]/(X^N + 1) Rt=Zt[x]/(XN+1)，其中 t t t 是明文模数，且 t < q t < q t<q。

单密钥 BFV 由五个算法组成：

1. B F V . S e t u p ( 1 λ ) → p p \mathrm{BFV.Setup(1^{\lambda})} → pp BFV.Setup(1λ)→pp：输入安全参数 λ \lambda λ，设置 RLWE 维度 N N N、密文模数 q q q、明文模数 t t t、密钥分布 φ \varphi φ 和 RLWE 误差分布 χ \chi χ。输出公共参数 p p pp pp： p p = { N , q , t , φ , χ } pp=\{N,q,t,\varphi,\chi\} pp={N,q,t,φ,χ}
2. B F V . S e c K e y G e n ( p p ) → s k \mathrm{BFV . SecKeyGen(pp)} → sk BFV.SecKeyGen(pp)→sk：输入安全参数 λ \lambda λ，采样 s ← R 3 s ← \mathcal{R}_3 s←R3。输出秘钥 s k sk sk： s k = s sk=s sk=s
3. B F V . P u b K e y G e n ( p p , s k ) → p k \mathrm{BFV . PubKeyGen(pp, sk)} → pk BFV.PubKeyGen(pp,sk)→pk：采样 a ∈ R q a \in \mathcal{R}_q a∈Rq 和 e ← χ e ← \chi e←χ。输出公钥 p k pk pk： p k = ( p 0 , p 1 ) = ( [ − ( s ⋅ a + e ) ] q , a ) pk=(p_0,p_1)=([-(s\cdot a+e)]_q,a) pk=(p0,p1)=([−(s⋅a+e)]q,a)
4. B F V . E n c r y p t ( p p , p k , m ) → c t \mathrm{BFV.Encrypt(pp, pk, m)} → ct BFV.Encrypt(pp,pk,m)→ct：输入明文 m m m，采样 u ← R 3 u ← \mathcal{R}_3 u←R3 和 e 0 e_0 e0、 e 1 ← χ e_1 ← \chi e1←χ。计算 Δ = q / t \Delta = q/t Δ=q/t。输出密文 c t ct ct： c t = ( c 0 , c 1 ) = ( [ Δ [ m ] t + u p 0 + e 0 ] q , [ u p 1 + e 1 ] q ) ∈ R q 2 ct=(c_0,c_1)=([\Delta[m]_t+up_0+e_0]_q,[up_1+e_1]_q)\in\mathcal{R}_q^2 ct=(c0,c1)=([Δ[m]t+up0+e0]q,[up1+e1]q)∈Rq2
5. B F V . D e c r y p t ( p p , s k , c t ) → m \mathrm{BFV . Decrypt(pp, sk, ct)} → m BFV.Decrypt(pp,sk,ct)→m：解密密文 c t ct ct 得到明文 m m m： m = [ ⌊ t ⋅ [ c 0 + c 1 s ] q q ⌉ ] t m=\left[\left\lfloor\frac{t\cdot[c_0+c_1s]_q}{q}\right\rceil\right]_t m=[⌊qt⋅[c0+c1s]q⌉]t
   为了改进单密钥BFV的缺陷，多密钥BFV（MK-BFV）被提出，持在不同密钥下加密的密文。

假设有 k k k 个参与方，每个参与方都有一个索引 i i i（ 1 ≤ i ≤ k 1 ≤ i ≤ k 1≤i≤k）及其公钥和私钥。多密钥BVF由以下算法组成：

1. M K - B F V . S e t u p ( 1 λ ) → p p \mathrm{MK\text{-}BFV.Setup(1^{\lambda})} → pp MK-BFV.Setup(1λ)→pp：运行 B F V . S e t u p ( 1 λ ) \mathrm{BFV.Setup(1^{\lambda})} BFV.Setup(1λ) 并输出公共参数 p p pp pp。
2. M K - B F V . K e y G e n ( p p ) → { s k i , p k i } \mathrm{MK\text{-}BFV. KeyGen(pp)}→\{sk_i, pk_i\} MK-BFV.KeyGen(pp)→{ski,pki}：每个参与方 i i i 分别通过 s k i ← B F V . S e c K e y G e n ( p p ) sk_i ← \mathrm{BFV.SecKeyGen(pp)} ski←BFV.SecKeyGen(pp) 和 p k i ← B F V . P u b K e y G e n ( p p , s k ) pk_i ← \mathrm{BFV . PubKeyGen(pp, sk)} pki←BFV.PubKeyGen(pp,sk) 生成其私钥和公钥。
3. M K - B F V . E n c r y p t ( p p , p k i , m i ) → c t ˉ i \mathrm{MK\text{-}BFV . Encrypt(pp, pk_i, m_i)}→ \bar{ct}i MK-BFV.Encrypt(pp,pki,mi)→ctˉi：每个参与方 i i i 生成 BFV 密文，表示为 c t i = ( c i , 0 , c i , 1 ) ← B F V . E n c r y p t ( p p , p k i , m i ) ct_i = (c{i,0}, c_{i,1}) ← \mathrm{BFV.Encrypt(pp, pk_i, m_i)} cti=(ci,0,ci,1)←BFV.Encrypt(pp,pki,mi)。然后将 c t i ct_i cti 转换为密文 c t ˉ i \bar{ct}i ctˉi： c t ‾ i = ( c i , 0 , c ˉ i , 1 , ... , c ˉ i , k ) ∈ R q k + 1 \overline{ct}i=(c{i,0},\bar{c}{i,1},\ldots,\bar{c}{i,k})\in\mathcal{R}q^{k+1} cti=(ci,0,cˉi,1,...,cˉi,k)∈Rqk+1其中 c ˉ i , j = { c i , 1 i f j = i , 0 otherwise. \bar{c}{i,j}= \begin{cases} c{i,1} & \mathrm{if~}j=i, \\ 0 & \text{otherwise.} & \end{cases} cˉi,j={ci,10if j=i,otherwise.

c t ˉ i \bar{ct}i ctˉi 是这样构建的：客户端 i i i 首先把 c i , 0 c{i,0} ci,0 放置在 c t ˉ i \bar{ct}i ctˉi 的 0 索引位置，然后把 c i , 1 c{i,1} ci,1 放置在 c t ˉ i \bar{ct}_i ctˉi 的 i i i 号索引位置，其他位置置为0。

4. M K - B F V . D e c r y p t ( p p , c t ˉ i , s k 1 , ... , s k k ) → m i \mathrm{MK\text{-}BFV . Decrypt(pp, \bar{ct}i, sk_1, \dots, sk_k)} → m_i MK-BFV.Decrypt(pp,ctˉi,sk1,...,skk)→mi：输入密文 c t ˉ i \bar{ct}i ctˉi，输出明文 m i m_i mi： m i = [ ⌊ t ⋅ [ c i , 0 + ∑ j = 1 k c ˉ i , j ⋯ k j ] q q ⌉ ⌋ t m_i=\left[\left\lfloor\frac{t\cdot\left[c{i,0}+\sum{j=1}^k\bar{c}_{i,j}\cdots k_j\right]_q}{q}\right\rceil\right\rfloor_t mi= qt⋅[ci,0+∑j=1kcˉi,j⋯kj]q t
5. M K - B F V . A d d ( p p , c t ˉ 0 , c t ˉ 1 ) → c t a d d \mathrm{MK\text{-}BFV . Add(pp, \bar{ct}0, \bar{ct}1)} → ct{add} MK-BFV.Add(pp,ctˉ0,ctˉ1)→ctadd：给定两个密文： c t ˉ 1 = ( c 1 , 0 , c 1 , 1 , 0 , ... , 0 ) ∈ R q k + 1 \bar{ct}1 = (c{1,0}, c{1,1}, 0, \dots, 0) \in \mathcal{R}q^{k+1} ctˉ1=(c1,0,c1,1,0,...,0)∈Rqk+1 和 c t ˉ 2 = ( c 2 , 0 , 0 , c 2 , 1 , 0 , ... , 0 ) ∈ R q k + 1 \bar{ct}2 = (c{2,0}, 0, c{2,1}, 0, \dots, 0) \in \mathcal{R}q^{k+1} ctˉ2=(c2,0,0,c2,1,0,...,0)∈Rqk+1，输出密文 c t a d d ct{add} ctadd： c t a d d = ( [ c 1 , 0 + c 2 , 0 ] q , c 1 , 1 , c 2 , 1 , 0 , ... , 0 ) ∈ R q k + 1 ct_{add}=([c_{1,0}+c_{2,0}]q,c{1,1},c_{2,1},0,\ldots,0)\in\mathcal{R}_q^{k+1} ctadd=([c1,0+c2,0]q,c1,1,c2,1,0,...,0)∈Rqk+1

Paillier 加密系统

Paillier密码系统是一种基于 复合剩余类 问题的半同态加密算法，支持加法同态运算。主要由密钥生成、加密、解密和同态加四个算法组成。

多项式插值

多项式插值是一种利用区间内若干 已知点 处的函数值，通过多项式来近似函数 f ( x ) f(x) f(x) 的方法。假设有 z + 1 z+1 z+1 个不同的点对： { ( x i , f ( x i ) ) } i = 1 z \{(x_i,f(x_i))\}{i=1}^z {(xi,f(xi))}i=1z，可以构造出一个阶为 z z z 的多项式： P ( x ) = a k x k + a k − 1 x k − 1 + ⋯ + a 0 P(x)=a_kx^k+a{k-1}x^{k-1}+\dots+a_0 P(x)=akxk+ak−1xk−1+⋯+a0

其中满足 f ( x i ) = P ( x i ) f(x_i)=P(x_i) f(xi)=P(xi)。

常用的插值方法有拉格朗日插值和牛顿插值。本文使用的是牛顿插值法。

实体和威胁模型

SAMK 的系统模型如下图所示：

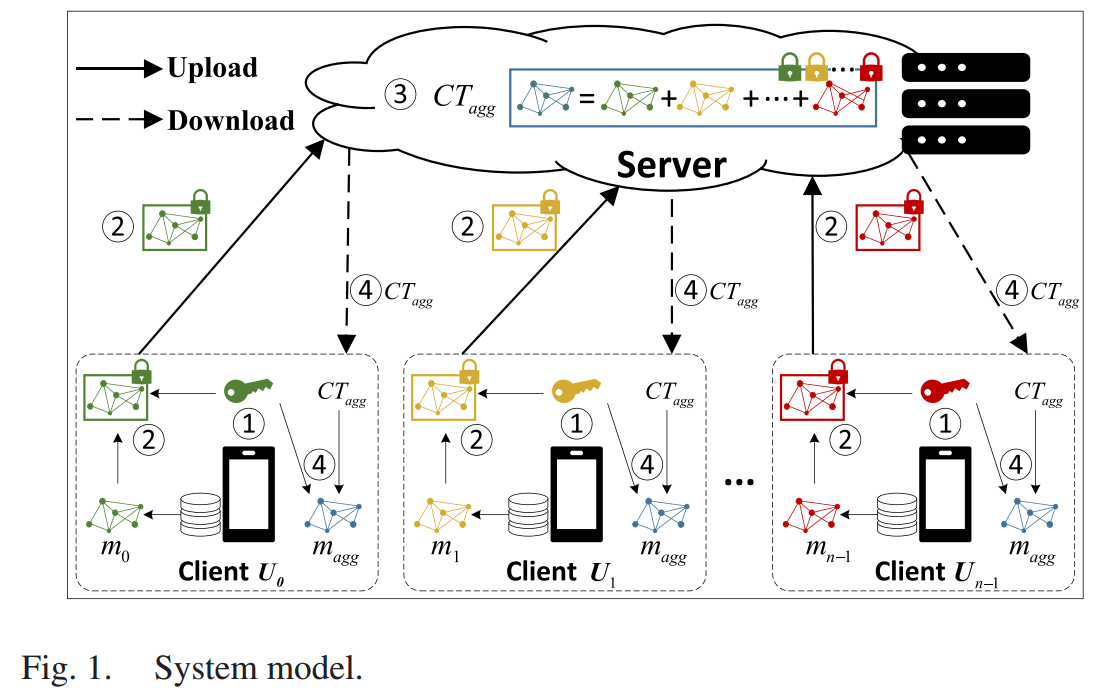
SAMK 包含一个服务器和 n n n 个客户端 U i ∈ [ 0 , n − 1 ] U_{i \in [0,n-1]} Ui∈[0,n−1]。

• 每个客户端 U i U_i Ui 生成其自身的公钥和私钥（步骤 1）。 U i U_i Ui 使用公钥对模型更新 m i m_i mi 进行加密（步骤 ©2），并在从服务器下载聚合密文 C T a g g CT_{agg} CTagg 后，使用私钥对其进行解密以获得聚合结果 m a g g m_{agg} magg（步骤 4）。
• 服务器初始化系统参数，聚合客户端的密文（步骤 3）。
• 此外，客户端可能在上传密文之前或之后掉线，本文的解决方案是服务器只聚合收集到的密文，然后发回在线客户端。

威胁模型

• 服务器和客户端都是诚实但好奇的，这意味着他们会诚实地执行协议，但会尝试推断和分析接收到的消息或公开可用的密文；
• 客户端可能会尝试通过推断其他客户端的模型更新来获取其敏感信息；
• 本文假设客户端与服务器之间不存在共谋，但客户端之间可能会共谋，以共同推断非共谋客户端的敏感信息；
• 此外，客户端与服务器之间的所有通信渠道都是不安全的，任何实体（服务器、客户端和外部人员）都可以拦截传输的信息。

SAMK

如何实现多密钥下的客户端单独解密

在多密钥BFV加密系统下，每个客户端 U i U_i Ui 拥有自己的公私钥 ( p k i , s k i ) (pk_i,sk_i) (pki,ski)，并且利用公钥 p k i pk_i pki 加密模型更新 m i m_i mi 得到密文： c t = ( c i , 0 , c i , 1 ) = ( [ Δ [ m i ] t + u i p i , 0 + e i , 0 ] q , [ u i p i , 1 + e i , 1 ] q ) ct=(c_{{i},0},c_{{i},1})=([{\Delta}[m_i]t+u_ip{{i},0}+e_{{i},0}]q,[u_ip{{i},1}+e_{{i},1}]_q) ct=(ci,0,ci,1)=([Δ[mi]t+uipi,0+ei,0]q,[uipi,1+ei,1]q)

作者察觉到，如果想用每个客户端的私钥都能解密聚合密文 C T a g g CT_{agg} CTagg，可以通过构造多项式，基于 RLWE 的密码系统的密文正是多项式形式，只要每个客户端都能构造出这个多项式，便能实现单独解密。

作者首先构造一个 f i ( x ) = s k i ⋅ c i , 1 = s i [ u i p i , 1 + e i , 1 ] q f_i(x)=sk_i\cdot c_{i,1}=s_i[u_ip_{i,1}+e_{i,1}]q fi(x)=ski⋅ci,1=si[uipi,1+ei,1]q，这样解密 m i m_i mi 就转换为了： m i = [ ⌊ t ⋅ [ c i , 0 + f i ( x ) ] q q ⌉ ] t m_i=\left[\left\lfloor\frac{t\cdot\left[c{i,0}+f_i(x)\right]_q}{q}\right\rceil\right]_t mi=[⌊qt⋅[ci,0+fi(x)]q⌉]t

同样地，解密聚合密文就转化为了： m a g g = [ ⌊ t ⋅ [ C T a g g + F ( x ) ] q q ⌉ ] t m_{agg}=\left[\left\lfloor\frac{t\cdot\left[CT_{agg}+F(x)\right]_q}{q}\right\rceil\right]_t magg=[⌊qt⋅[CTagg+F(x)]q⌉]t

其中 m a g g = [ ∑ i = 0 n − 1 m i ] t m_{agg}=[\sum_{i=0}^{n-1} m_i]t magg=[∑i=0n−1mi]t， C T a g g = [ ∑ i = 0 n − 1 c i , 0 ] q CT{agg}=[\sum_{i=0}^{n-1} c_{i,0}]q CTagg=[∑i=0n−1ci,0]q， F ( x ) = ∑ i = 0 n − 1 f i ( x ) F(x)=\sum{i=0}^{n-1}f_i(x) F(x)=∑i=0n−1fi(x)。

作者利用 N N N 个点来构造多项式： Poly.Inter ( ( x 0 , F ( x 0 ) ) , ( x 1 , F ( x 1 ) ) , ... , ( x N − 1 , F ( x N − 1 ) ) ) → F ( x ) \text{Poly.Inter}((x_0,F(x_0)),(x_1,F(x_1)),\ldots,(x_{N-1},F(x_{N-1})))\to F(x) Poly.Inter((x0,F(x0)),(x1,F(x1)),...,(xN−1,F(xN−1)))→F(x)

SAMK 框架主要有五个阶段：setup ，keygen ，encrypt ，aggregate 和 decrypt。

SAMK 的加解密和聚合的细节图如下所示：

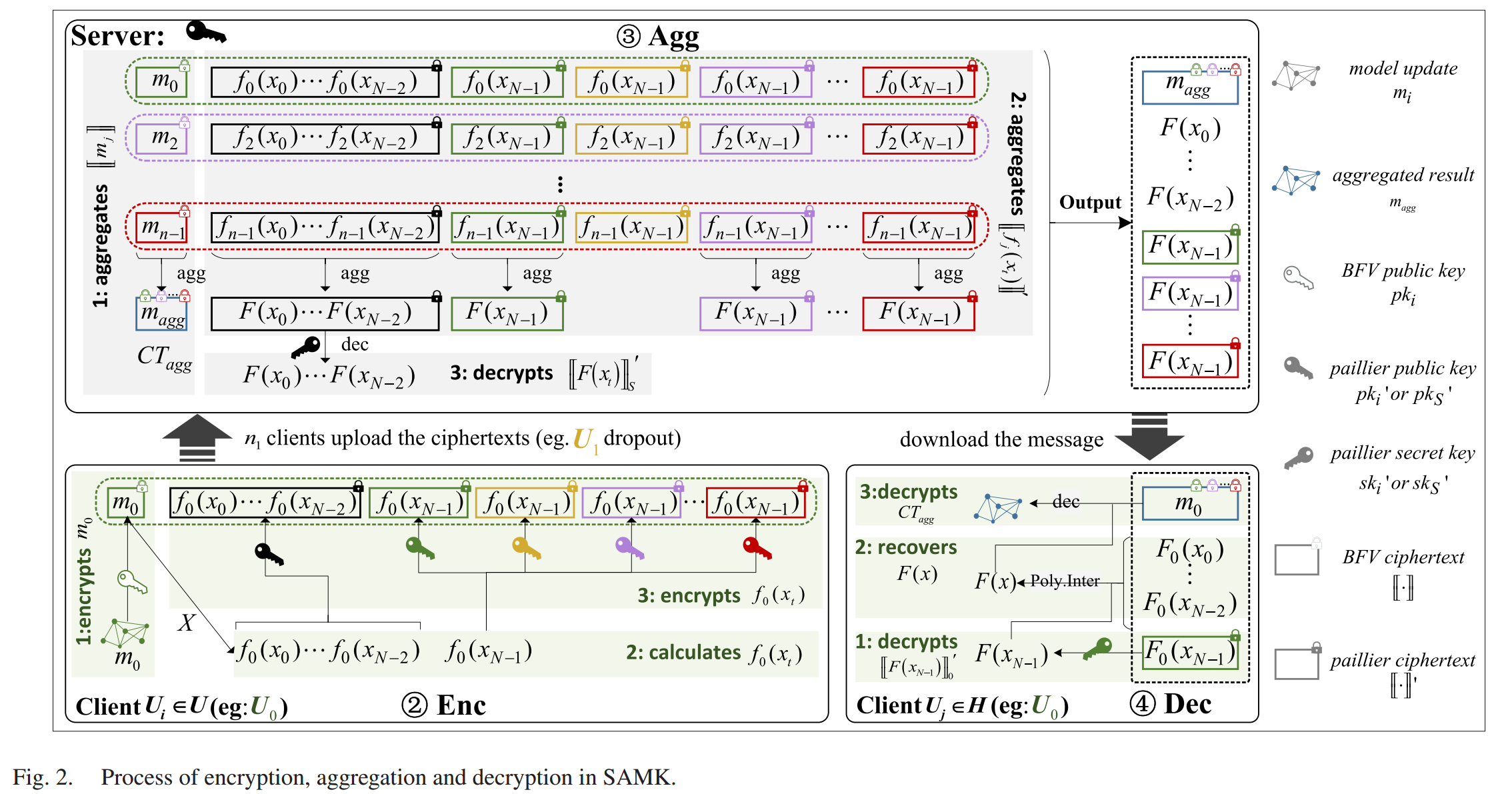
建立阶段

在建立阶段，服务器初始化 BFV 和 Paillier 加密系统的安全参数，并生成自变量集合 X = x 0 , x 1 , ... , x N − 1 X={x_0,x_1,\dots,x_{N-1}} X=x0,x1,...,xN−1 和公共参数 P P PP PP。具体细节如算法 1 所示。

其中 Paillier 的安全参数 κ \kappa κ 是密钥的位长度，为了确保 Paillier 加密不越界，应该保证 ( q − 1 ) ⋅ ( x max ⁡ N − 1 ) x max ⁡ − 1 < 2 2 κ \frac{(q-1)\cdot(x_{\max}^{N}-1)}{x_{\max}-1}<2^{2\kappa} xmax−1(q−1)⋅(xmaxN−1)<22κ，其中 x m a x x_{max} xmax 是 X X X 中的最大元素，比较符左侧表示 f i ( x ) f_i(x) fi(x) 中的最大多项式值。

密钥生成

客户端 U i U_i Ui 独立生成自己的 BFV 密钥对 ( p k i , s k i ) (pk_i, sk_i) (pki,ski) 和 Paillier 密钥对 ( p k i ′ , s k i ′ ) (pk_i^{\prime}, sk_i^{\prime}) (pki′,ski′)。服务器独立生成自己的 Paillier 密钥对 ( p k S ′ , s k S ′ ) (pk_S^{\prime}, sk_S^{\prime}) (pkS′,skS′) 。

在所有实体生成其密钥后，它们会广播用于加密的 Paillier 公钥。BFV 公钥主要用于加密模型更新，而 Paillier 公钥主要用于加密 BFV 密文的多项式值。

加密

在加密过程中，每个客户端 U i U_i Ui 使用 BFV 对 m i m_i mi 进行加密，并使用 Paillier 对 BFV 密文的 N N N 个多项式值进行加密。其中， N − 1 N − 1 N−1 个值使用服务器的 Paillier 公钥加密，剩余的一个值使用 所有客户端 的 Paillier 公钥加密。作者使用 [ [ ⋅ ] ] [[·]] [[⋅]] 和 [ [ ⋅ ] ] ′ [[·]]^′ [[⋅]]′ 分别表示模型更新和多项式值的密文。

加密可以分为四个步骤进行：

1. 客户端 U i U_i Ui 使用其自身的 BFV 公钥 p k i pk_i pki 对其模型更新 m i m_i mi 进行加密，得到密文 [ [ m i ] ] [[m_i]] [[mi]]。
2. U i U_i Ui 使用 s k i sk_i ski 和 c i c_i ci 计算多项式 f i ( x ) = s k i ⋅ c i , 1 f_i(x) = sk_i \cdot c_{i,1} fi(x)=ski⋅ci,1。
3. 使用 X X X 中的 N N N 个值作为自变量，计算 f i ( x ) f_i(x) fi(x) 的 N N N 个不同值： f i ( x 0 ) f_i(x_0) fi(x0)、 f i ( x 1 ) f_i(x_1) fi(x1) 、... 、 f i ( x N − 1 ) f_i(x_{N−1}) fi(xN−1)。
4. 对于前 N − 1 N-1 N−1 个值， U i U_i Ui 使用服务器的 Paillier 公钥 p k S ′ pk_S^′ pkS′ 对它们进行加密，得到密文： [ [ f i ( x 0 ) ] ] S ′ [[f_i(x_0)]]S^′ [[fi(x0)]]S′ 、 [ [ f i ( x 1 ) ] ] S ′ [[f_i(x_1)]]S^′ [[fi(x1)]]S′ 、...、 [ [ f i ( x N − 2 ) ] ] S ′ [[f_i(x{N−2})]]S^′ [[fi(xN−2)]]S′。对于 f i ( x N − 1 ) f_i(x{N−1}) fi(xN−1)， U i U_i Ui 使用每个客户端 U v ∈ U U_v \in U Uv∈U 的 Paillier 公钥 p k v ′ pk_v^′ pkv′ 对其进行加密，得到密文： [ [ f i ( x N − 1 ) ] ] 0 ′ [[f_i(x{N−1})]]0^′ [[fi(xN−1)]]0′ 、 [ [ f i ( x N − 1 ) ] ] 1 ′ [[f_i(x{N−1})]]1^′ [[fi(xN−1)]]1′ 、...、 [ [ f i ( x N − 1 ) ] ] n − 1 ′ [[f_i(x{N−1})]]_{n−1}^′ [[fi(xN−1)]]n−1′。

加密完成后，每个客户端将所有密文发送给服务器进行聚合，客户端存在掉线，服务器会收到来自 n 1 n_1 n1 个客户端的信息，将这些客户端集合记为 H , ∣ H ∣ = n 1 H,|H|=n_1 H,∣H∣=n1。

优化计算开销

我们知道，模型更新可以展开为一个 l l l 维向量 m i = { m i , 0 , m i , 1 , ... , m i , l − 1 } m_i=\{m_{i,0},m_{i,1},\dots,m_{i,l-1}\} mi={mi,0,mi,1,...,mi,l−1}，其中每个数都是小bits数值，而 BFV 的明文空间容量是很大的，所以我们可以使用打包技术，将多个参数打包进一个明文中，从而减少密文数量。

假设一个 BFV 明文多项式最多可以容纳 M M M 个数据；将 M M M 个模型参数编码到一个明文中可以一次性加密它们。每个客户端的 BFV 密文可以被简化为 l / M l/M l/M。

而在 Paillier 加密系统中，明文空间 N S N_S NS 可以容纳 k k k 条信息，其中 k k k 满足： ∑ t = 0 k − 1 ∣ f i ( x t ) ∣ ≤ ∣ N S ∣ \sum_{t=0}^{k-1}|f_i(x_t)|\leq|N_S| ∑t=0k−1∣fi(xt)∣≤∣NS∣，其中 ∣ N S ∣ |N_S| ∣NS∣ 和 ∣ f i ( x t ) ∣ |f_i(x_t)| ∣fi(xt)∣ 分别表示对应的位长度。因此每个客户端可以将 k k k 个明文打包成一个明文以提高效率。

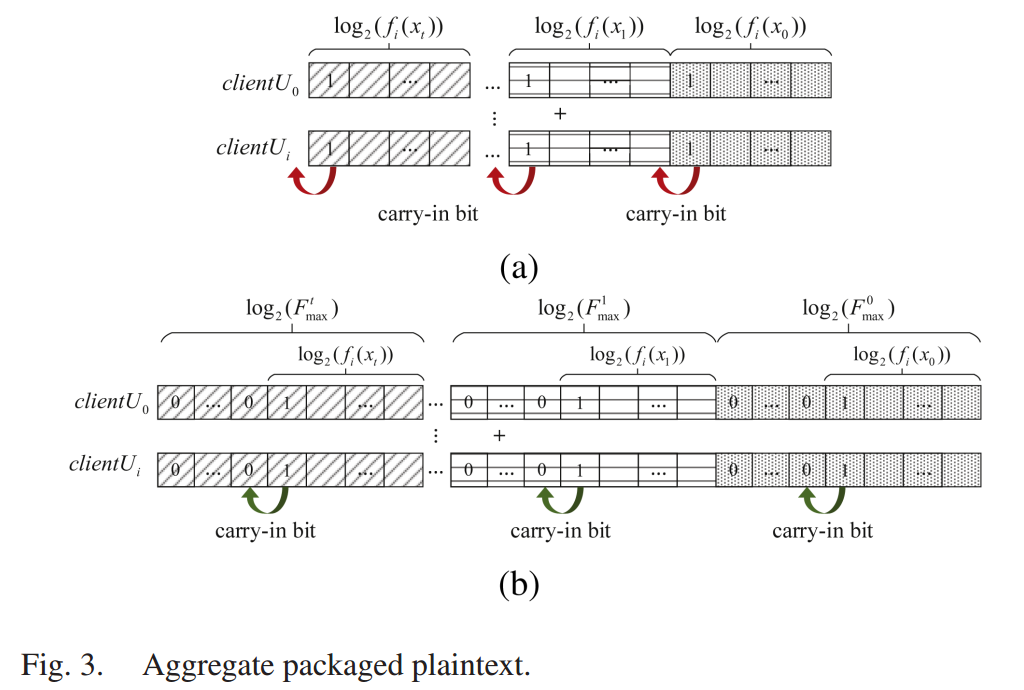
但是我们知道，数值的相加会产生进位，为了防止越界，需要为每个明文分配足够的空间，本文为每个明文 f i ( x t ) f_i(x_t) fi(xt) 分配 ∣ F m a x t ∣ |F_{max}^t| ∣Fmaxt∣ 的位空间，其中 F m a x t F_{max}^t Fmaxt 是 n n n 个客户端的 f i ( x t ) f_i(x_t) fi(xt) 的最大可能聚合结果。

聚合

在聚合过程中，服务器对模型更新的密文 { [ [ m j ] ] } j = 0 n 1 − 1 \{[[m_j]]\}{j=0}^{n_1−1} {[[mj]]}j=0n1−1 和多项式值的密文 { { [ [ f j ( x t ) ] ] S ′ } t = 0 N − 2 , { [ [ f j ( x N − 1 ) ] ] i ′ } i = 0 n − 1 } j = 0 n 1 − 1 \{\{[[f_j (x_t )]]S^′ \}{t=0}^{N−2} , \{[[f_j (x{N−1})]]i^′\}{i=0}^{n−1}\}{j=0}^{n_1−1} {{[[fj(xt)]]S′}t=0N−2,{[[fj(xN−1)]]i′}i=0n−1}j=0n1−1 执行同态加法运算。然后，它解密下标为 S S S 的聚合后的密文以获得 N − 1 N−1 N−1 个多项式值 { F ( x t ) } t = 0 N − 2 \{F (x_t)\}{t=0}^{N−2} {F(xt)}t=0N−2。

如算法4所示，聚合阶段主要包括3个步骤。

1. 服务器聚合所有客户端的 [ [ m j ] ] [[m_j]] [[mj]] 以获得聚合密文 C T a g g CT_{agg} CTagg。
2. 服务器分别聚合所有客户端的密文 [ [ f j ( x 0 ) ] ] S ′ [[f_j (x_0)]]_S^{\prime} [[fj(x0)]]S′ ， [ [ f j ( x 1 ) ] ] S ′ [[f_j (x_1)]]S^{\prime} [[fj(x1)]]S′ ，...， [ [ f j ( x N − 2 ) ] ] S ′ [[f_j (x{N−2})]]_S^{\prime} [[fj(xN−2)]]S′，以获得聚合密文 [ [ F ( x 0 ) ] ] S ′ [[F(x_0)]]_S^{\prime} [[F(x0)]]S′ ， [ [ F ( x 1 ) ] ] S ′ [[F(x_1)]]S^{\prime} [[F(x1)]]S′ ，...， [ [ F ( x N − 2 ) ] ] S ′ [[F(x{N−2})]]_S^{\prime} [[F(xN−2)]]S′：

\[ F ( x 0 ) \] \] S ′ = \[ \[ f 0 ( x 0 ) \] \] S ′ ⋅ ... ⋅ \[ \[ f n 1 − 1 ( x 0 ) \] \] S ′ m o d N S 2 \[ \[ F ( x 1 ) \] \] S ′ = \[ \[ f 0 ( x 1 ) \] \] S ′ ⋅ ... ⋅ \[ \[ f n 1 − 1 ( x 1 ) \] \] S ′ m o d N S 2 \[ \[ F ( x N − 2 ) \] \] S ′ = \[ \[ f 0 ( x N − 2 ) \] \] S ′ ⋅ ... ⋅ \[ \[ f n 1 − 1 ( x N − 2 ) \] \] S ′ m o d N S 2 \\begin{align} \[\[F(x_0)\]\]_S\^{\\prime} \& =\[\[f_0(x_0)\]\]_S\^{\\prime}\\cdot\\ldots \\cdot \[\[f_{n_1-1}(x_0)\]\]_S\^{\\prime}\\ \\mathrm{mod}\\ {N_S}\^2 \\notag\\\\ \[\[F(x_1)\]\]_S\^{\\prime} \& =\[\[f_0(x_1)\]\]_S\^{\\prime}\\cdot\\ldots\\cdot \[\[f_{n_1-1}(x_1)\]\]_S\^{\\prime}\\ \\mathrm{mod}\\ {N_S}\^2 \\notag\\\\ \[\[F(x_{N-2})\]\]_S\^{\\prime} \&=\[\[f_0(x_{N-2})\]\]_S\^{\\prime}\\cdot\\ldots\\cdot \[\[f_{n_1-1}(x_{N-2})\]\]_S\^{\\prime}\\ \\mathrm{mod}\\ {N_S}\^2 \\notag \\end{align} \[\[F(x0)\]\]S′\[\[F(x1)\]\]S′\[\[F(xN−2)\]\]S′=\[\[f0(x0)\]\]S′⋅...⋅\[\[fn1−1(x0)\]\]S′ mod NS2=\[\[f0(x1)\]\]S′⋅...⋅\[\[fn1−1(x1)\]\]S′ mod NS2=\[\[f0(xN−2)\]\]S′⋅...⋅\[\[fn1−1(xN−2)\]\]S′ mod NS2 然后服务器将所有客户端的密文 \[ \[ f j ( x N − 1 ) \] \] 0 ′ \[\[f_j (x_{N−1})\]\]_0\^{\\prime} \[\[fj(xN−1)\]\]0′, \[ \[ f j ( x N − 1 ) \] \] 1 ′ \[\[f_j (x_{N−1})\]\]_1\^{\\prime} \[\[fj(xN−1)\]\]1′, ..., \[ \[ f j ( x N − 1 ) \] \] n 1 − 1 ′ \[\[f_j (x_{N−1})\]\]_{n_1−1}\^{\\prime} \[\[fj(xN−1)\]\]n1−1′ 分别聚合，以获得聚合密文 \[ \[ F ( x N − 1 ) \] \] 0 ′ \[\[F(x_{N−1})\]\]_0\^{\\prime} \[\[F(xN−1)\]\]0′, \[ \[ F ( x N − 1 ) \] \] 1 ′ \[\[F(x_{N−1})\]\]_1\^{\\prime} \[\[F(xN−1)\]\]1′, ..., \[ \[ F ( x N − 1 ) \] \] n 1 − 1 ′ \[\[F(x_{N−1})\]\]_{n_1−1}\^{\\prime} \[\[F(xN−1)\]\]n1−1′： \[ F ( x N − 1 ) \] \] 0 ′ = \[ \[ f 0 ( x N − 1 ) \] \] 0 ′ ⋅ ... ⋅ \[ \[ f n 1 − 1 ( x N − 1 ) \] \] 0 ′ m o d N 0 2 \[ \[ F ( x N − 1 ) \] \] 1 ′ = \[ \[ f 0 ( x N − 1 ) \] \] 1 ′ ⋅ ... ⋅ \[ \[ f n 1 − 1 ( x N − 1 ) \] \] 1 ′ m o d N 1 2 \[ \[ F ( x N − 1 ) \] \] n 1 − 1 ′ = \[ \[ f 0 ( x N − 1 ) \] \] n 1 − 1 ′ ⋅ ... ⋅ \[ \[ f n 1 − 1 ( x N − 1 ) \] \] n 1 − 1 ′ m o d N n 1 − 1 2 \\begin{align} \[F(x_{N-1})\]\]_0\^{\\prime} \& =\[\[f_0(x_{N-1})\]\]_0\^{\\prime}\\cdot\\ldots\\cdot \[\[f_{n_1-1}(x_{N-1})\]\]_0\^{\\prime}\\mathrm{mod}{N_0}\^2\\\\ \[\[F(x_{N-1})\]\]_1\^{\\prime} \& =\[\[f_0(x_{N-1})\]\]_1\^{\\prime}\\cdot\\ldots\\cdot \[\[f_{n_1-1}(x_{N-1})\]\]_1\^{\\prime}\\mathrm{mod}{N_1}\^2\\\\ \[\[F(x_{N-1})\]\]_{n_1-1}\^{\\prime} \& =\[\[f_0(x_{N-1})\]\]_{n_1-1}\^{\\prime}\\cdot\\ldots\\cdot \[\[f_{n_1-1}(x_{N-1})\]\]_{n_1-1}\^{\\prime}\\mathrm{mod}{N_{n_1-1}}\^2 \\end{align} \[F(xN−1)\]\]0′\[\[F(xN−1)\]\]1′\[\[F(xN−1)\]\]n1−1′=\[\[f0(xN−1)\]\]0′⋅...⋅\[\[fn1−1(xN−1)\]\]0′modN02=\[\[f0(xN−1)\]\]1′⋅...⋅\[\[fn1−1(xN−1)\]\]1′modN12=\[\[f0(xN−1)\]\]n1−1′⋅...⋅\[\[fn1−1(xN−1)\]\]n1−1′modNn1−12 3. 最后，服务器使用其 Paillier 密钥 s k S sk_S skS 解密密文 \[ \[ F ( x 0 ) \] \] S ′ \[\[F(x_0)\]\]_S\^{\\prime} \[\[F(x0)\]\]S′、 \[ \[ F ( x 1 ) \] \] S ′ \[\[F(x_1)\]\]_S\^{\\prime} \[\[F(x1)\]\]S′、...、 \[ \[ F ( x N − 2 ) \] \] S ′ \[\[F(x_{N−2})\]\]_S\^{\\prime} \[\[F(xN−2)\]\]S′，以获得 F ( x 0 ) F(x_0) F(x0)、 F ( x 1 ) F(x_1) F(x1)、...、 F ( x N − 2 ) F(x_{N−2}) F(xN−2)。如果在加密中使用了打包技术，则在服务器解密多项式值的密文后，需要对明文进行解包。 然后服务器将聚合值发送给在线客户端，详细内容可见算法4：  #### 解密 在解密过程中，每个客户端 U j ∈ H U_j \\in H Uj∈H 都从服务器接收到消息 { C T a g g , F ( x 0 ) , F ( x 1 ) , ... , F ( x N − 2 ) , \[ \[ F ( x N − 1 ) \] \] j ′ } \\{CT_{agg}, F(x_0), F(x_1), \\dots, F(x_{N−2}), \[\[F(x_{N−1})\]\]_j\^′\\} {CTagg,F(x0),F(x1),...,F(xN−2),\[\[F(xN−1)\]\]j′}。 U j U_j Uj 能够独立解密 \[ \[ F ( x N − 1 ) \] \] j ′ \[\[F(x_{N−1})\]\]_j\^′ \[\[F(xN−1)\]\]j′，然后结合 F ( x N − 1 ) F(x_{N−1}) F(xN−1) 与 F ( x 0 ) F(x_0) F(x0)、 F ( x 1 ) F(x_1) F(x1)、...、 F ( x N − 2 ) F(x_{N−2}) F(xN−2)， U j U_j Uj 可以独立解密 C T a g g CT_{agg} CTagg 以获得聚合结果 m a g g m_{agg} magg。 如算法5所示，解密阶段分为三个步骤。 1. 客户端 U j U_j Uj 使用其Paillier密钥 s k j ′ sk_j\^{\\prime} skj′ 解密密文 \[ \[ F ( x N − 1 ) \] \] j ′ \[\[F(x_{N−1})\]\]_j\^{\\prime} \[\[F(xN−1)\]\]j′，以获得 F ( x N − 1 ) F(x_{N−1}) F(xN−1)。 2. 在获得 F ( x N − 1 ) F(x_{N−1}) F(xN−1) 后，结合接收到的 N − 1 N−1 N−1 个点 { F ( x t ) } t = 0 N − 2 \\{F(x_t)\\}_{t=0}\^{N−2} {F(xt)}t=0N−2，客户端 U j U_j Uj 总共拥有 N N N 个 F ( x ) F(x) F(x) 的点。客户端利用这 N N N 个点进行多项式插值以获得 F ( x ) F(x) F(x)。 3. 最后，客户端 U j U_j Uj 使用 F ( x ) F(x) F(x) 和 C T a g g CT_{agg} CTagg 获得聚合结果 m a g g m_{agg} magg 。如果在BFV加密中使用了批量编码，在解密聚合密文 C T a g g CT_{agg} CTagg 后，需要对明文 m a g g m_{agg} magg 进行解码以恢复所有模型参数。  ## 总结 ### 优点 * 做到多密钥环境下的"单轮、无交互聚合"； * 支持任意数量的客户端掉线； * 安全性强：服务器与客户端均无法恢复其他实体的更新； * 精确加解密； * 无需可信第三方、无需多服务器架构； ### 缺点 * 单轮通信量巨大，本文为了减少交互，却是以通信量为代价； * 每轮客户端不仅要计算 BFV ，还要计算 Paillier ，计算开销也不低； * 多项式插值的计算开销也不小。