引言
前序学习进程中,已将掌握了卷积效果非线性处理|非负性的操作方法,引入非线性可以为后面的学习带来一些便利。
而在更早的学习中,我们已经掌握了基本池化操作组件的应用。
今天基于前序学习进度,尝试在非线性的基础上引入池化操作。
池化
池化的定义非常简单,在这里可以仿照卷积计算定义一个池化核,非常重要的是,池化核只需要定义核的高度和宽度,而不必写出具体的核元素。这是因为池化核各个位置的元素可以取任何值,但这些值不会参与实际运算,所有不必去定义这些元素。
基于这一层理解,可以再简化一些,与其说是池化核,不如说是池化框,只需要用这个池化框逐个选中矩阵,然后对选中矩阵的元素进行取极大值或者平均值即可。
实操
还是以之前的运算代码为基础,增添池化操作的核心代码。
如果单独对池化操作感兴趣,可以从基本池化操作组件回忆。
这是新增的池化操作代码:
python
# 定义池化功能函数
def manual_pooling(input_feature, pool_kernel_size=2, pool_stride=2, pool_type='max'):
"""
手动实现池化操作
参数:
input_feature: 输入特征图(2D数组)
pool_kernel_size: 池化核大小(默认2×2)
pool_stride: 滑动步长(默认2)
pool_type: 池化类型('max' 最大池化 / 'avg' 平均池化)
返回:
output: 池化后的输出特征图
"""
# 获取输入特征图尺寸
h, w = input_feature.shape
# 计算输出特征图尺寸(向下取整,不考虑填充)
pool_out_h = (h - pool_kernel_size) // pool_stride + 1
pool_out_w = (w - pool_kernel_size) // pool_stride + 1
# 定义池化效果储存矩阵
pool_patch=torch.zeros((pool_out_h,pool_out_w),dtype=torch.float32)
# 开展池化操作
# 使用for循环逐个选取矩阵
for i in range(pool_out_h):
for j in range(pool_out_w):
pool_h_start=i*pool_stride
pool_h_end=pool_h_start+pool_kernel_size
pool_w_start=j*pool_stride
pool_w_end=pool_w_start+pool_kernel_size
# 获得当前窗口
pool_window=input_feature[pool_h_start:pool_h_end,pool_w_start:pool_w_end]
# 池化,取最大值
pool_patch[i,j] = pool_window.max()
return pool_patch
pool_output=manual_pooling(relu_manual, pool_kernel_size=2, pool_stride=2, pool_type='max')
print('pool_output=',pool_output)代码运行后:
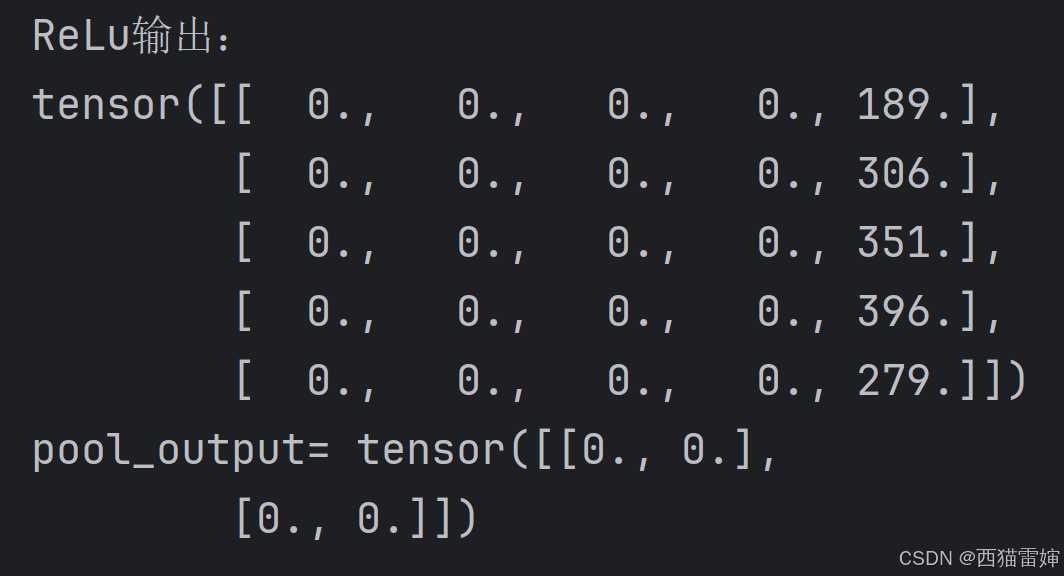
这里可以看到pool_output 是一个2行2列矩阵,这是因为ReLu是一个5行5列矩阵,pool_kernel大小是2,pool_stride=2,所以(5-2)/2+1=2。
然后把pool_stride改为1,这里直接给出完整代码:
python
import torch
# 1. 定义原始输入(3通道5×5)和卷积核1(边缘检测核)
input_tensor = torch.tensor([
# 输入通道1(R):5×5
[
[1, 2, 3, 4, 5],
[6, 7, 8, 9, 10],
[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25]
],
# 输入通道2(G):5×5
[
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35],
[36, 37, 38, 39, 40],
[41, 42, 43, 44, 45],
[46, 47, 48, 49, 50]
],
# 输入通道3(B):5×5
[
[51, 52, 53, 54, 55],
[56, 57, 58, 59, 60],
[61, 62, 63, 64, 65],
[66, 67, 68, 69, 70],
[71, 72, 73, 74, 75]
]
], dtype=torch.float32) # 形状:(3,5,5)
# 输出原始通道的形状
input_tensor_channels,input_tensor_h,input_tensor_w=input_tensor.shape
print('input_tensor_channels=',input_tensor_channels)
print('input_tensor_h=',input_tensor_h)
print('input_tensor_w=',input_tensor_w)
# 卷积核1(边缘检测核):3个子核,每个3×3
kernel1 = torch.tensor([
[[1, 0, -1], [1, 0, -1], [1, 0, -1]], # 子核1(R通道)
[[1, 0, -1], [1, 0, -1], [1, 0, -1]], # 子核2(G通道)
[[1, 0, -1], [1, 0, -1], [1, 0, -1]] # 子核3(B通道)
], dtype=torch.float32) # 形状:(3,3,3)
# 输出卷积核的形状
kernel1_channels,kernel1_h,kernel1_w=kernel1.shape
print('kernel1_channels=',kernel1_channels)
print('kernel1_h=',kernel1_h)
print('kernel1_w=',kernel1_w)
# 通过循环自动计算卷积值
# 定义步长为1
stride=1
# 定义卷积运算后的输出矩阵大小
out_h=(input_tensor_h-kernel1_h)//stride+1
out_w=(input_tensor_w-kernel1_w)//stride+1
# 为避免对原始矩阵造成破坏,新定义一个量来完全复制原始矩阵
input_cal_tensor=input_tensor
# 输出矩阵里面是所有卷积运算的效果,这个矩阵比原始矩阵小,先定义为纯0矩阵
output_cal_tensor=torch.zeros((out_h,out_w),dtype=torch.float32)
# 循环计算
for i in range(out_h):
for j in range(out_w):
# 对原始矩阵取块进行计算,这里定义了取块的起始行
in_h_start=i*stride
# 取块的末行
in_h_end=in_h_start+kernel1_h
# 取块的起始列
in_w_start=j*stride
# 取块的末列
in_w_end=in_w_start+kernel1_w
# 这是取到的块
input_patch=input_cal_tensor[:,in_h_start:in_h_end,in_w_start:in_w_end]
# 定义一个空列表output_cal存储数据
output_cal = []
for k in range(input_tensor_channels):
# k代表了通道数,因为每个通道都要进行卷积运算,
# 因此需要先得到单通道的计算效果,然后把它们储存在列表中
output_channel=(input_patch[k]*kernel1[k]).sum()
#print('input_patch[',k,']=',input_patch[k])
#print('output_patch[', k, ']=', kernel1[k])
# 计算结果储存在列表中
output_cal.append(output_channel)
# 把通道效果叠加后,保存到卷积输出矩阵
# 这里有3层,第一层是每一个子卷积核和原始矩阵的每一个通道进行卷积运算
# 第二层是将第一层的卷积运算值按照顺序排放在列表output_cal中
# 第三层再将列表中获得数据直接叠加,获得当下卷积运算的总值
# 综合起来,卷积核和每一通道内的对应块对位相乘,然后全部求和,输出给当前记录卷积值的矩阵
# 由于每一个i和j都会对应k个通道,所以使用了3层循环来表达
output_cal_tensor[i, j] = sum(output_cal)
#print('output_cal_tensor[', i, j, ']=', output_cal_tensor[i, j])
print('output=',output_cal_tensor)
# 扩充原始矩阵,周围补一圈0
padding=1
padded_h=input_tensor_h+2*padding
padded_w=input_tensor_w+2*padding
padded_input_tensor = torch.zeros((input_tensor_channels,padded_h,padded_w),dtype=torch.float32)
padded_input_tensor[:,padding:-padding,padding:-padding]=input_tensor
print(padded_input_tensor)
# 对扩充后的矩阵卷积运算
# 计算卷积矩阵大小
padded_out_h=(padded_h-kernel1_h)//stride+1
padded_out_w=(padded_w-kernel1_w)//stride+1
# 为避免对原始矩阵造成破坏,新定义一个量来完全复制原始矩阵
padded_input_cal_tensor=padded_input_tensor
# 输出矩阵里面是所有卷积运算的效果,这个矩阵比原始矩阵小,先定义为纯0矩阵
padded_output_cal_tensor=torch.zeros((padded_out_h,padded_out_w),dtype=torch.float32)
for i in range(padded_out_h):
for j in range(padded_out_w):
# 对原始矩阵取块进行计算,这里定义了取块的起始行
in_h_start=i*stride
# 取块的末行
in_h_end=in_h_start+kernel1_h
# 取块的起始列
in_w_start=j*stride
# 取块的末列
in_w_end=in_w_start+kernel1_w
# 这是取到的块
input_patch=padded_input_cal_tensor[:,in_h_start:in_h_end,in_w_start:in_w_end]
# 定义一个空列表output_cal存储数据
output_cal = []
for k in range(input_tensor_channels):
# k代表了通道数,因为每个通道都要进行卷积运算,
# 因此需要先得到单通道的计算效果,然后把它们储存在列表中
output_channel=(input_patch[k]*kernel1[k]).sum()
#print('input_patch[',k,']=',input_patch[k])
#print('output_patch[', k, ']=', kernel1[k])
# 计算结果储存在列表中
output_cal.append(output_channel)
# 把通道效果叠加后,保存到卷积输出矩阵
# 这里有3层,第一层是每一个子卷积核和原始矩阵的每一个通道进行卷积运算
# 第二层是将第一层的卷积运算值按照顺序排放在列表output_cal中
# 第三层再将列表中获得数据直接叠加,获得当下卷积运算的总值
# 综合起来,卷积核和每一通道内的对应块对位相乘,然后全部求和,输出给当前记录卷积值的矩阵
# 由于每一个i和j都会对应k个通道,所以使用了3层循环来表达
padded_output_cal_tensor[i, j] = sum(output_cal)
#print('padded_output_cal_tensor[', i, j, ']=', padded_output_cal_tensor[i, j])
print('padded_output=',padded_output_cal_tensor)
# 使卷积计算的负值为0,正值不变
# 初始化全0矩阵,使其和卷积计算的结果矩阵大小一致
relu_manual=torch.zeros_like(padded_output_cal_tensor)
for i in range(padded_output_cal_tensor.shape[0]):
for j in range(padded_output_cal_tensor.shape[1]):
relu_manual[i,j]=torch.max(torch.tensor(0.0),padded_output_cal_tensor[i,j])
print('ReLu输出:')
print(relu_manual)
# 简洁代码
# 初始化全0矩阵,使其和卷积计算的结果矩阵大小一致
#relu_manual_s=torch.zeros_like(padded_output_cal_tensor)
relu_manual_s=torch.max(torch.tensor(0.0),padded_output_cal_tensor)
print('ReLu输出:')
print(relu_manual_s)
# 定义池化功能函数
def manual_pooling(input_feature, pool_kernel_size=2, pool_stride=1, pool_type='max'):
"""
手动实现池化操作
参数:
input_feature: 输入特征图(2D数组)
pool_kernel_size: 池化核大小(默认2×2)
pool_stride: 滑动步长(默认2)
pool_type: 池化类型('max' 最大池化 / 'avg' 平均池化)
返回:
output: 池化后的输出特征图
"""
# 获取输入特征图尺寸
h, w = input_feature.shape
# 计算输出特征图尺寸(向下取整,不考虑填充)
pool_out_h = (h - pool_kernel_size) // pool_stride + 1
pool_out_w = (w - pool_kernel_size) // pool_stride + 1
print(pool_out_h)
# 定义池化效果储存矩阵
pool_patch=torch.zeros((pool_out_h,pool_out_w),dtype=torch.float32)
# 开展池化操作
# 使用for循环逐个选取矩阵
for i in range(pool_out_h):
for j in range(pool_out_w):
pool_h_start=i*pool_stride
pool_h_end=pool_h_start+pool_kernel_size
pool_w_start=j*pool_stride
pool_w_end=pool_w_start+pool_kernel_size
# 获得当前窗口
pool_window=input_feature[pool_h_start:pool_h_end,pool_w_start:pool_w_end]
# 池化,取最大值
pool_patch[i,j] = pool_window.max()
return pool_patch
pool_output=manual_pooling(relu_manual, pool_kernel_size=2, pool_stride=1, pool_type='max')
print('pool_output=',pool_output)代码运行的实际效果为:
ReLu输出:
tensor([[ 0., 0., 0., 0., 189.],
0., 0., 0., 0., 306.\], \[ 0., 0., 0., 0., 351.\], \[ 0., 0., 0., 0., 396.\], \[ 0., 0., 0., 0., 279.\]\]) 4 pool_output= tensor(\[\[ 0., 0., 0., 306.\], \[ 0., 0., 0., 351.\], \[ 0., 0., 0., 396.\], \[ 0., 0., 0., 396.\]\])
细节说明
这里比较粗糙的选用了最大值池化,也可以使用平均值池化。
由于池化单独定义了函数,需要修改池化步长pool_stride时,最好把pool_output=manual_pooling(relu_manual, pool_kernel_size=2, pool_stride=1, pool_type='max')这一行的pool_stride参数提前修改,如果只修改def manual_pooling(input_feature, pool_kernel_size=2, pool_stride=1, pool_type='max')这一行代码,不会有实际效果。
总结
学习了卷积运算效果的池化处理,取到了卷积运算后的最大值。