1 向平衡因子不为零的节点的树中插入新节点
- 平衡二叉树 :是一种二叉排序树,要求每个节点的 "左子树高度 - 右子树高度"(即平衡因子)的绝对值不超过 1(平衡因子只能是 - 1、0、1)。
- 插入新节点的影响:插入节点会让某条路径的子树高度 + 1,可能导致祖先节点的平衡因子超出范围(变成 - 2 或 2),此时才需要 "平衡旋转" 来恢复平衡。
题目分析 :
题目说**"向平衡因子不为零的节点的树中插入新节点,必引起平衡旋转"**
但实际情况是:插入后,该节点的平衡因子可能只是从 - 1/1 变成 0(比如左子树高度 + 1,让原本平衡因子为 1 的节点,左、右子树高度相等),此时平衡因子仍符合要求,不需要旋转。
所以插入新节点后,不一定会触发平衡旋转,题目说法错误。
2 B-树 的插入算法

- B 树的核心特点 :B 树是一种多路平衡查找树(不是二叉树),要求每个节点的子节点数量(以及关键字数量)在规定范围内(比如 m 阶 B 树,每个节点的关键字数要在
⌈m/2⌉-1到m-1之间)。 - B 树的插入逻辑 :当插入一个关键字导致某个节点的关键字数超过上限(比如 m 阶 B 树节点关键字数达到 m),就会触发节点分裂:把这个节点从中间分成两个节点,中间的关键字向上移动到父节点中。
题目分析 :
普通平衡树(比如平衡二叉树)需要专门的 "旋转" 操作来维持平衡;而 B 树的 "分裂" 操作本身,会让节点的关键字数和子节点数始终保持在规定范围内,自然维持了树的平衡结构 ------ 相当于用 "向上分裂" 代替了专门的平衡调整。
所以题目说法是正确的。
B 树是一种多路平衡查找树(不是二叉树,每个节点可以有多个子节点),常用在数据库、文件系统的索引结构中(比如 MySQL 的 InnoDB 引擎就用 B 树的变种 B + 树做索引)。
3 个核心特点:
- 多路结构:假设是 "m 阶 B 树"(m 是阶数,比如 m=3),每个节点可以存多个关键字(比如 m=3 时,每个节点最多存 2 个关键字),同时有多个子节点(最多 3 个子节点)。
- 平衡特性:B 树的所有叶子节点都在同一层(树的高度是平衡的),不需要像平衡二叉树那样用旋转维持平衡。
- 插入 / 删除的 "分裂 / 合并" :
- 插入时,若节点关键字数超过上限,就把节点从中间 "分裂",中间关键字上移到父节点;
- 删除时,若节点关键字数不足下限,就和兄弟节点 "合并",并调整父节点的关键字。
这两个操作天然维持了树的平衡,不用额外调整。
简单说,B 树是为了让 "磁盘等外部存储设备" 快速查找数据设计的 ------ 多路结构减少了磁盘 IO 次数,平衡特性保证了查找效率稳定。
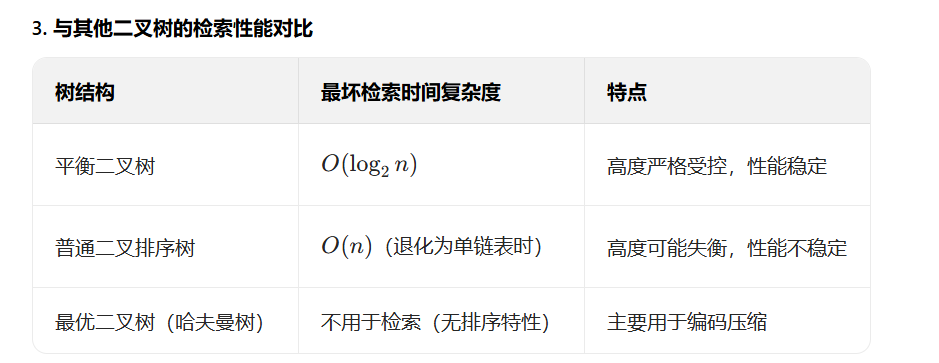
3 平衡二叉树的检索性能


核心知识点


4 二叉排序树检索效率和树高


5 二叉排序树 & 遍历
比如一棵二叉排序树:
根节点是 5,左子树是 3(3的左子树是2、右子树是4),右子树是7(7的右子树是8)。
这棵树的结构是:
5
/ \
3 7
/ \ \
2 4 8- 前序遍历 (根→左→右):
5 → 3 → 2 → 4 → 7 → 8(先根后左,不是从小到大) - 中序遍历 (左→根→右):
2 → 3 → 4 → 5 → 7 → 8(正好是从小到大的序列)
1. 二叉排序树的定义
- 规则:左子树所有节点值 < 根节点值 < 右子树所有节点值(左右子树也需满足此规则)。
2. 三种遍历方式(以示例树 5(3(2,4),7(,8)) 为例)
| 遍历方式 | 顺序 | 遍历结果(示例树) | 是否有序(从小到大) |
|---|---|---|---|
| 前序遍历 | 根 → 左子树 → 右子树 | 5 → 3 → 2 → 4 → 7 → 8 | ❌ (先根后左,无序) |
| 中序遍历 | 左子树 → 根 → 右子树 | 2 → 3 → 4 → 5 → 7 → 8 | ✅ (二叉排序树的特性) |
| 后序遍历 | 左子树 → 右子树 → 根 | 2 → 4 → 3 → 8 → 7 → 5 | ❌ (后访问根,无序) |
3. 关键结论
- 唯一能让二叉排序树得到有序序列的遍历方式是:中序遍历。
6 负载因子影响 "碰撞概率"(α 越小概率越低),但不能彻底避免碰撞

先搞懂两个概念:
- 散列表(哈希表):用 "哈希函数" 把数据映射到数组位置(叫 "散列地址")来存储,比如把 "学号 1001" 映射到数组下标 1。
- 负载因子 α :公式是
α = 已存储的元素个数 / 散列表的数组长度→ 代表散列表的 "装满程度",α 越小越空。
题目说法是错的!
负载因子 α<1,只是说明 "散列表没装满",但无法避免碰撞 。
"碰撞" 是指:两个不同的数据,通过哈希函数算出了同一个散列地址(比如学号 1001 和 2001,哈希函数取最后一位,都映射到下标 1)。
哪怕 α 很小(比如散列表长度是 100,只存了 1 个元素,α=0.01),只要哈希函数设计得不够好,就可能出现两个元素映射到同一地址 → 碰撞还是会发生。
简单说:负载因子影响 "碰撞概率"(α 越小概率越低),但不能彻底避免碰撞。
7 哈希表解决 "碰撞"(多个数据映射到同一地址)

先明确:哈希表的 "节点结构" 分不同实现方式
哈希表解决 "碰撞"(多个数据映射到同一地址)的方法主要有两种,对应的节点结构不一样:
-
开放定址法 :
碰撞时,通过 "找下一个空位置" 来存数据(比如当前位置被占了,就看下一个下标)。
这种方式的哈希表节点,确实只存数据元素自身(不需要指针)。
-
链地址法(拉链法) :
碰撞时,把同一地址的所有数据存在一个 "链表" 里。
这种方式的哈希表节点,不仅要存数据元素,还得包含 "指向下一个节点的指针"(用来连链表)。
题目说法是错的!
因为哈希表有 "链地址法" 这种实现方式,它的节点是包含指针的。
题目说 "只包含数据自身、不含任何指针",把情况说死了,所以不对。
8 线性探测法

首先解释线性探测法 :
它是哈希表解决冲突的一种方法。当插入元素时,若哈希函数计算的地址已被占用,则依次检查下一个地址(地址 + 1,超出表长则循环到开头),直到找到空地址;"搜索次数" 指从初始地址开始,尝试的地址数量(包括最终成功存放的地址)。
接下来解这道题:
已知:哈希表地址区间 0-17(共 18 个单元),哈希函数H(K)=K mod 17,关键字序列:26,25,72,38,8,18,59。
步骤 1:依次计算前 6 个关键字的哈希地址,并处理冲突
- 26 :
26 mod 17 = 9→ 地址 9(空),直接存入,搜索次数 1。 - 25 :
25 mod 17 = 8→ 地址 8(空),直接存入,搜索次数 1。 - 72 :
72 mod 17 = 72-4×17=72-68=4→ 地址 4(空),直接存入,搜索次数 1。 - 38 :
38 mod 17 = 38-2×17=4→ 地址 4(已被 72 占用,冲突)。
线性探测:地址 4→5(空),存入地址 5,搜索次数 2。 - 8 :
8 mod 17 = 8→ 地址 8(已被 25 占用,冲突)。
线性探测:地址 8→9(已被 26 占用)→10(空),存入地址 10,搜索次数 3。 - 18 :
18 mod 17 = 1→ 地址 1(空),直接存入,搜索次数 1。
步骤 2:计算 59 的哈希地址,处理冲突并统计搜索次数
59 :59 mod 17 = 59-3×17=59-51=8 → 初始地址 8。
线性探测过程:
- 地址 8(被 25 占用)→ 第 1 次尝试
- 地址 9(被 26 占用)→ 第 2 次尝试
- 地址 10(被 8 占用)→ 第 3 次尝试
- 地址 11(空)→ 第 4 次尝试,成功存入。
因此,存放元素 59 需要搜索的次数是4。

解析:
"同义词" 指多个关键字的哈希地址相同,线性探测法下,这 k 个关键字会依次占用连续的地址:
- 第 1 个同义词:直接存入初始地址,探测次数为 1;
- 第 2 个同义词:冲突后探测下 1 个地址,探测次数为 2;
- 第 3 个同义词:冲突后探测下 2 个地址,探测次数为 3;
- ......
- 第 k 个同义词:探测次数为 k。
因此,总探测次数是 D 。
补充说明:
该结论的前提是 "哈希表初始为空,且同义词的初始地址无其他元素占用",此时探测次数最少(无额外冲突)。
9 二次探测法

一、二次探测法介绍
二次探测法是哈希表解决冲突的一种方法:当关键字通过哈希函数得到的初始地址H0被占用时,依次尝试地址H0 ± 1², H0 ± 2², H0 ± 3²,...(需保证地址在哈希表区间内),直到找到空地址。
二、题目解答步骤
已知:
- 哈希表长 = 14(地址区间:0~13)
- 哈希函数:
H(key) = key % 11 - 已存关键字:15、38、61、84
- 待插入关键字:49
步骤 1:计算 49 的初始哈希地址
H(49) = 49 % 11 = 5(因为 11×4=44,49-44=5)。
步骤 2:检查初始地址是否被占用
先计算已存关键字的哈希地址,确认地址 5 是否被占用:
- 15:
15%11=4→ 地址 4 - 38:
38%11=5→ 地址 5(已被占用,冲突)
步骤 3:用二次探测法找空地址
二次探测的地址公式为:Hi = (H0 ± i²) % 表长(i 从 1 开始)。
- i=1 :
- 尝试
H0 + 1² = 5 + 1 = 6→ 检查地址 6:未被占用?
先确认已存关键字的地址:- 61:
61%11=6→ 地址 6(被占用,冲突)
- 61:
- 再尝试
H0 - 1² = 5 - 1 = 4→ 地址 4(被 15 占用,冲突)
- 尝试
- i=2 :
- 尝试
H0 + 2² = 5 + 4 = 9→ 检查地址 9:
已存关键字 84 的地址:84%11=7(11×7=77,84-77=7)→ 地址 7,地址 9 未被占用。
- 尝试
因此,49 最终放入的位置是9。
答案:D
10 哈希查找

一、哈希查找的核心概念
- 链地址法(拉链法) :
把哈希地址相同的元素存在同一个链表中(每个哈希地址对应一个链表)。 - 聚集现象 :
哈希表中元素集中在某一区域的现象(会降低查找效率)。 - 再哈希法 :
冲突时用多个哈希函数,依次计算地址直到找到空位置。
二、逐个分析题目中的 4 个说法
(1)"采用链地址法解决冲突时,查找一个元素的时间是相同的"
- 错误。
链地址法中,不同链表的长度可能不同:若某个哈希地址的链表很长,查找该链表中元素的时间会比短链表的元素长。
(2)"采用链地址法解决冲突时,若插入规定总是在链首,则插入任一个元素的时间是相同的"
- 正确。
插入到链首只需修改新节点的指针指向原链首,再将哈希地址指向新节点,操作时间与链表长度无关,因此插入时间相同。
(3)"用链地址法解决冲突易引起聚集现象"
- 错误。
链地址法中,冲突元素是分散在不同链表中的,不会集中在哈希表的某一区域,因此不会引起聚集现象(聚集是开放定址法的问题)。
(4)"再哈希法不易产生聚集"
- 错误。
再哈希法本质是开放定址法的一种,冲突时会依次尝试新地址,仍可能出现元素集中在某一区域的情况,因此仍易产生聚集。
三、结论
不正确的说法是(1)(3)(4),共 3 个。
答案:C
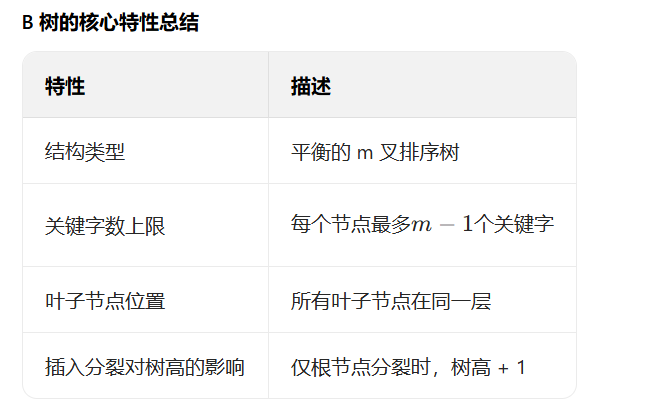
11 B - 树

B - 树的核心属性
m 阶 B - 树是一种m 叉平衡排序树,需满足两个关键特征:
- m 叉树:每个节点最多有 m 个子节点(对应最多有\(m-1\)个关键字);
- 平衡排序树 :
- 排序性:节点内的关键字有序,且子树的关键字与父节点关键字满足大小关系;
- 平衡性:所有叶子节点在同一层,避免了树的高度失衡。



12 B 树和 B + 树
一、B 树(也叫 B - 树)
可以理解为 "多叉平衡排序树",核心特点:
- 每个节点存关键字 + 子节点指针;
- 关键字在节点中有序排列,子树的关键字与父节点关键字满足大小关系;
- 所有叶子节点在同一层(平衡);
- 适合随机查找,但顺序查找(比如找 "比 x 大的所有元素")需要逐层遍历,效率低。
二、B + 树(B 树的变种)
是 "带叶子节点链表的 B 树",核心特点:
- 非叶子节点只存 "索引关键字"(不存数据),数据只存在叶子节点;
- 所有叶子节点按关键字有序链接成链表;
- 既支持随机查找(和 B 树一样从根节点找),也支持高效的顺序查找(直接遍历叶子链表);
- 是数据库、文件系统索引的常用结构(比如 MySQL 的 InnoDB 索引)。
一句话总结区别:
B 树 "节点存数据 + 索引",适合随机查;B + 树 "叶子存数据 + 链表",同时支持随机查和顺序查。
13 m 阶 B 树的核心定义


14 平衡二叉树(AVL 树)

一、基础概念
- 平衡二叉树(AVL 树) :是二叉排序树,且每个节点的平衡因子(左子树高度 - 右子树高度)的绝对值不超过 1。
- 不平衡调整 :插入节点后,若某节点平衡因子绝对值 > 1,则需通过 "旋转" 调整。调整类型由 "最低不平衡节点 A" 的左 / 右子树 及子树的不平衡方向决定,分为 4 种:LL、LR、RR、RL。
二、4 种调整类型的判断逻辑
调整类型的命名规则:
- 第一个字母:最低不平衡节点 A 的不平衡侧(左子树失衡→L,右子树失衡→R);
- 第二个字母:A 的失衡子树的失衡侧(子树的左子树失衡→L,子树的右子树失衡→R)。
三、题目分析
已知条件:
- 最低不平衡节点为 A;
- A 的左孩子平衡因子为 0(左孩子的左右子树高度相等);
- A 的右孩子平衡因子为 1 (右孩子的左子树比右子树高 1)→ 说明 A 的右子树失衡 ,且右子树的左子树失衡。
对应调整类型:
- 第一个字母:A 的失衡侧是 "右子树"→ R;
- 第二个字母:右子树的失衡侧是 "左子树"→ L;
因此调整类型为RL 型。
答案:C
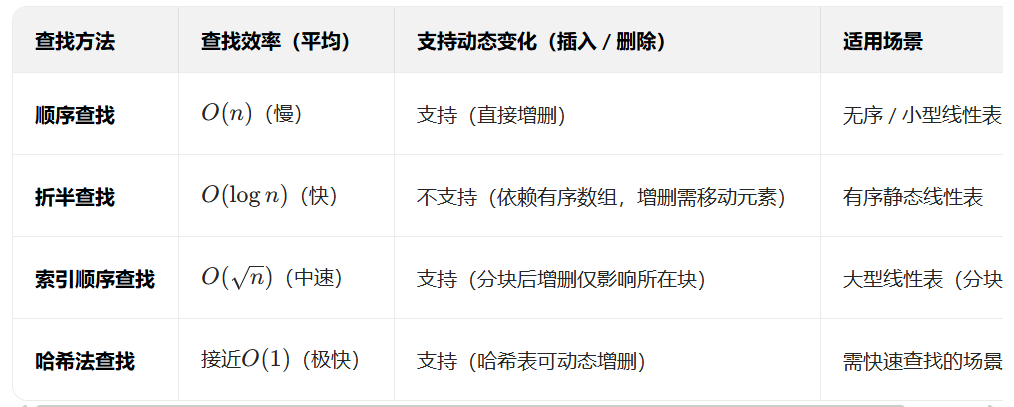
15 各查找方法的特性对比
16 分块查找的核心组织方式

分块查找的核心组织方式
分块查找将数据分为若干块,并满足两个关键条件:
- 块内无序:每一块内部的数据可以不按顺序排列;
- 块间有序:不同块之间必须有序(例如,第 1 块的所有数据都小于第 2 块的所有数据);
- 建立索引块:用 "每块的最大(或最小)数据" 组成一个索引表,通过索引表快速定位目标数据所在的块。
选项分析
- A 错误:分块查找不要求 "块内数据有序"。
- B 正确:符合分块查找 "块内无序、块间有序、用块的最大 / 最小数据做索引" 的核心组织方式。
- C 错误:分块查找不需要 "块内数据有序"。
- D 错误:分块查找不强制 "每块数据个数相同"(仅需合理分块即可)。
答案:B
17 二分查找的条件

二分查找的核心条件
- 表必须有序:数据需按关键字升序或降序排列;
- 表必须是顺序存储:因为二分查找需要通过 "下标" 随机访问中间元素,链表无法高效实现随机访问。
选项分析
- A 错误:二分查找不能用链表存储(链表无随机访问下标)。
- B 错误:二分查找对数据类型无限制,只要能比较大小即可(如字符串)。
- C 错误:表有序即可,升序或降序都可以(只需调整比较逻辑)。
- D 正确:符合 "表有序 + 顺序存储" 的核心条件。
答案:D
18 平均查找长度(ASL)的计算逻辑

顺序查找中,每个记录的查找长度(即查找该记录需要比较的次数)为:
- 第 1 个记录:查找长度 = 1
- 第 2 个记录:查找长度 = 2
- ...
- 第 n 个记录:查找长度 = n
