

💗博主介绍:计算机专业的一枚大学生 来自重庆 @燃于AC之乐✌专注于C++技术栈,算法,竞赛领域,技术学习和项目实战✌💗
💗根据博主的学习进度更新(可能不及时)
💗后续更新主要内容:C语言,数据结构,C++、linux(系统编程和网络编程)、MySQL、Redis、QT、Python、Git、爬虫、数据可视化、小程序、AI大模型接入,C++实战项目与学习分享。
👇🏻 精彩专栏 推荐订阅👇🏻
点击进入🌌作者专栏🌌:
Linux系统编程✅
算法画解✅
C++✅🌟算法相关题目点击即可进入实操🌟
感兴趣的可以先收藏起来,请多多支持,还有大家有相关问题都可以给我留言咨询,希望希望共同交流心得,一起进步,你我陪伴,学习路上不孤单!
文章目录
前言
这些题目摘录于洛谷,好题,典型的题,考察各类算法运用,可用于蓝桥杯及各类算法比赛备战,算法题目练习,提高算法能力,补充知识,提升思维。
锻炼解题思路,从学会算法模板后,会分析,用到具体的题目上。
对应题目点链接即可做。
本期涉及算法:模拟 + 优化,图的性质 + 并查集,暴力枚举 + 预处理 + 滑动窗口(优化),线性dp,前缀和 + 哈希表 + 同余,正难则反-反图。
题目清单
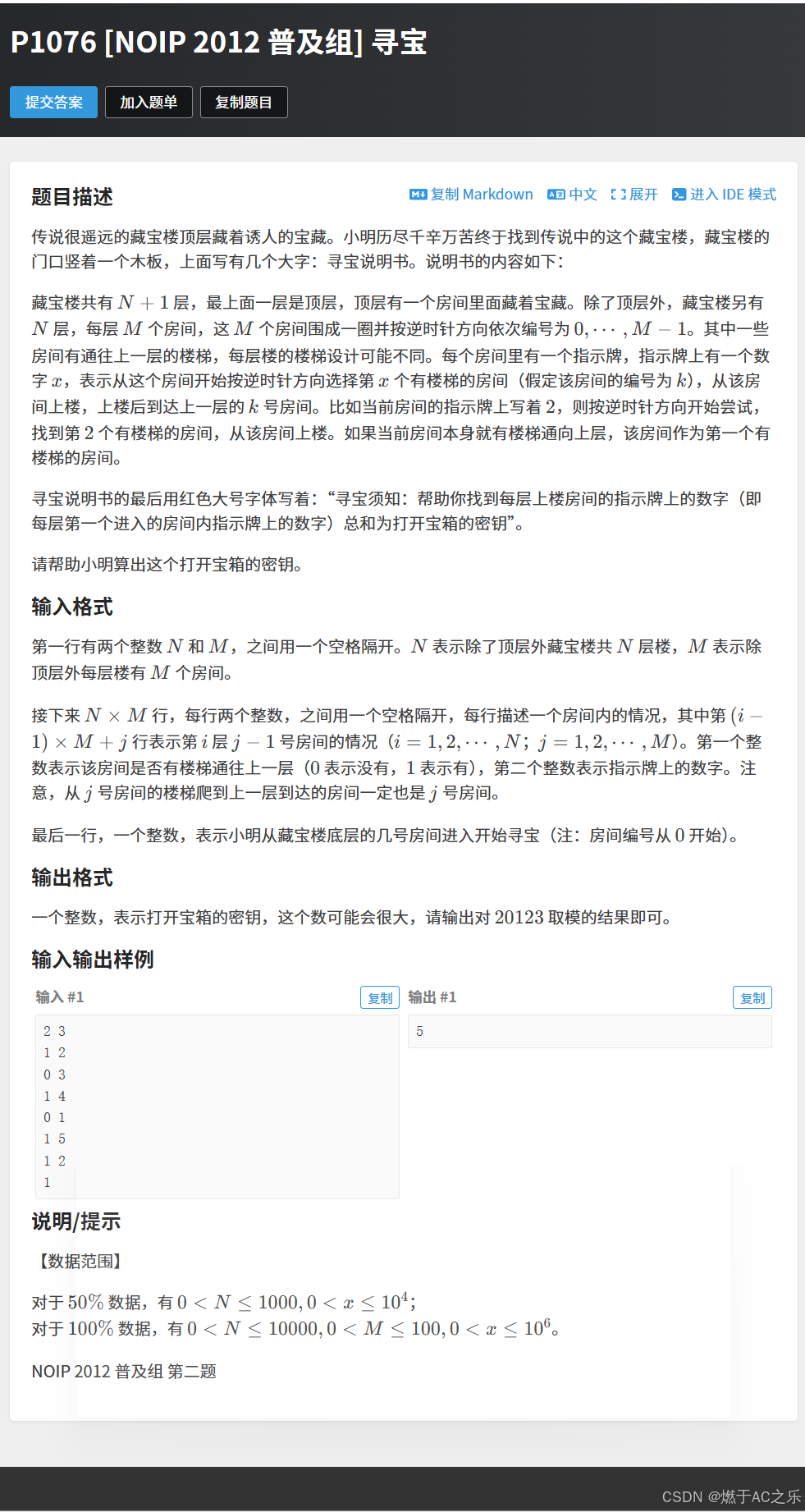
1.寻宝

解法:模拟 + 优化
根据题意模拟爬楼过程:
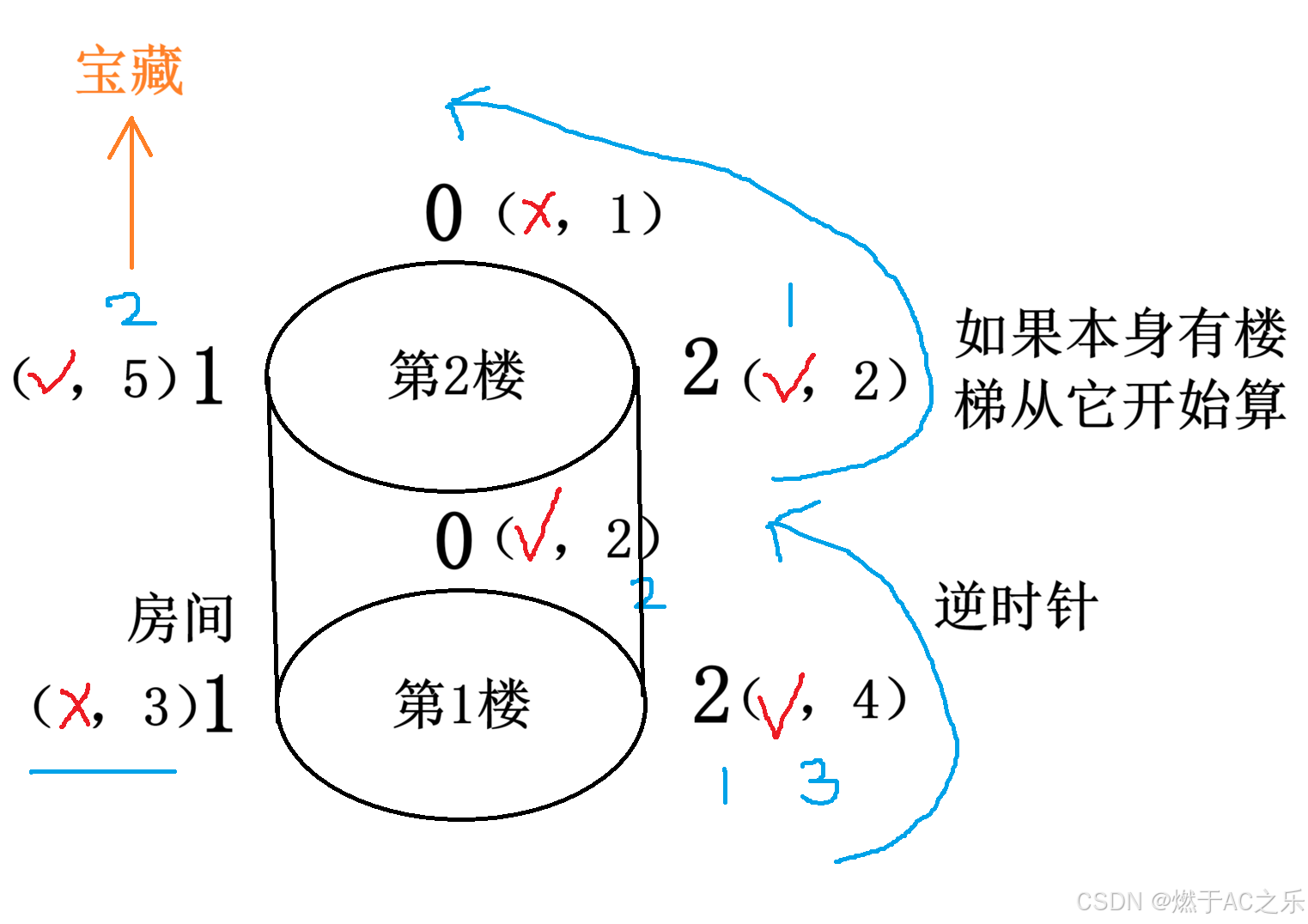
但是每层楼都去找那个房间的话,时间复杂度大,可以优化,用一个cnt[i]数组存:表示第i层楼有楼梯的房间数,用要找的第s个%cnt[i], 注意如果取模后=0,就是找第cnt[i]个符合要求的房间。
代码:
cpp
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1e4 + 10, M = 110, MOD = 20123;
LL n, m;
bool st[N][N]; //标记楼梯信息
LL s[N][M]; //维护指示牌信息
LL cnt[N]; //用于优化,存第 i 楼有楼梯的房间个数
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++)
{
for(int j = 0; j < m; j++) //注意:房间编号从0开始
{
int a, b; cin >> a >> b;
if(a)
{
st[i][j] = true;
cnt[i]++;
}
s[i][j] = b;
}
}
int pos = 0; cin >> pos;
LL ret = 0;
for(int i = 1; i <= n; i++)
{
ret = (ret + s[i][pos]) % MOD;
//优化
LL step = s[i][pos] % cnt[i];
if(!step) step = cnt[i]; //注意
while(1)
{
if(st[i][pos]) step--;
if(step == 0) break;
pos++;
if(pos == m) pos = 0; //走了一圈
}
}
cout << ret << endl;
return 0;
}2.村村通
题目: P1536 村村通
解法:图的性质 + 并查集
这道题要将已经连接好的部分城镇和未连接的城镇都连通(可以是间接连接),连接的边数 = 连通块的个数 - 1。那么,就用并查集维护连通的点。 输入多组数据按ctrl + z结束。
cpp
#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
int fa[N];
int find(int x)
{
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
void un(int x, int y)
{
fa[find(x)] = find(y);
}
int main()
{
while(cin >> n >> m)
{
for(int i = 1; i <= n; i++) fa[i] = i; //初始化
for(int i = 1; i <= m; i++)
{
int a, b; cin >> a >> b;
un(a, b);
}
int ret = 0;
for(int i = 1; i <= n; i++)
{
if(fa[i] == i) //有几个父结点,连通块
ret++;
}
cout << ret - 1 << endl;
}
return 0;
}3.Diamond Collector S
题目: P3143 [USACO16OPEN] Diamond Collector S
解法:暴力枚举 + 预处理 + 滑动窗口(优化)
错误的解法:贪心 + 滑动窗口,先选⼀段长度「最大」的,再选⼀段⻓度「次大」的。但是这样是错误的,因为第⼀次
的选择会影响 第⼆次的选择,两者加起来「不⼀定是最优」的。比如: [1, 1, 4, 5, 6, 7, 8, 10], k = 3
如果先选 [4, 5, 6, 7] ,接下来只能选 [1, 1] 或者 [8, 10] ,总长就是 6 ;
但是如果先选 [5, 6, 7, 8] ,接下来可以选 [1, 1, 4] ,总长就是 7。
因此,先选⼀段最长,再选⼀段次长的方法是不对的。
两个同时要考虑:
那么我们可以 「枚举」所有的情况,以 i 位置为「分界点」,「左边」选⼀段,「右边」选⼀段:
左边选:[1, i - 1] 区间内,符合要求的 「最长子串」 的长度。
右边选: [1, n] 区间内,符合要求的 「最长子串」 的长度。
这样我们就可以枚举出所有的情况,「左右两部分相加」的最大值(max) 就是结果。
接下来考虑,如何快速找到[1, i - 1]区间内,符合要求的「最长子串」的长度以及[i, n]区间内,符
合要求的「最长子串」的长度,类似动态规划预处理:
数组f[i]表示[1, i]区间的最长长度,g[i]表示[i, n]区间的最长长度;
对于f[i],先找出 [1, i - 1] 区间的最长度,然后再找到 [以a[i]为结尾位置」 的最长子串的
长度,两者最大值即可;
对于g[i],先找出 [i + 1, n] 区间的最长度,然后再找到 「以a[i[为起始位置」 的最长子串的
长度,两者最大值即可。
如何找出 「以 a [i] 为结尾位置」 的最长子串的长度:
在滑动窗口的过程中,我们每次找到⼀段「符合要求的子串」时,都可以知道这段⼦串的终止位置right。
因此,做⼀次「滑动窗口」,就可以把所有位置的信息都「预处理」出来。
「以 a [i] 为起始位置」 的最长子串的长度,倒着再来⼀次即可。
代码:
cpp
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 5e4 + 10;
int n, k;
int a[N];
int f[N], g[N];
int main()
{
cin >> n >> k;
for(int i = 1; i <= n; i++) cin >> a[i];
sort(a + 1, a + 1 + n);
//预处理[1, i]
for(int left = 1, right = 1; right <= n; right++)
{
while(a[right] - a[left] > k) left++;
f[right] = max(f[right - 1], right - left + 1);
}
//预处理[i, n]
for(int left = n, right = n; left >= 1; left--)
{
while(a[right] - a[left] > k) right--;
g[left] = max(g[left + 1], right - left + 1);
}
int ret = 0;
for(int i = 2; i <= n; i++)
{
ret = max(ret, f[i - 1] + g[i]);
}
cout << ret << endl;
return 0;
}4.Apple Catching G
题目: P2690 [USACO04NOV] Apple Catching G
解法:线性dp
1.状态表示:
f[i] [j] :当时间为 i 时,移动次数为 j 时,能拿到的最⼤分数。
2.状态转移方程:
先计算当前这个时刻,移动 j 次之后,能否拿到苹果:
如果 j % 2 == 0 && a[i] == 1 或者 j % 2 == 1 && a[i] == 2 ,那就能拿到,c = 1 ;
否则拿不到, c = 0 。
当前这个时刻和上⼀个时刻的位置不同: f[i - 1] [j - 1] + c;
当前这个时刻和上⼀个时刻的位置⼀样: f[i - 1] [j] + c.
3.最终结果:
f[n]这⼀行中的最大值。
cpp
#include <iostream>
using namespace std;
const int N = 1010, M = 50;
int n, m;
int a[N];
int f[N][M];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> a[i];
for(int i = 1; i <= n; i++)
{
for(int j = 0; j <= m; j++)
{
int c = 0;
if(j % 2 == 0 && a[i] == 1 || (j % 2 == 1 && a[i] == 2)) c = 1;
f[i][j] = f[i - 1][j] + c;
if(j) f[i][j] = max(f[i][j], f[i - 1][j - 1] + c);
}
}
int ret = 0;
for(int j = 0; j <= m; j++)
{
ret = max(f[n][j], ret);
}
cout << ret << endl;
return 0;
}5.Subsequences Summing to Sevens S
题目: P3131 [USACO16JAN] Subsequences Summing to Sevens (区间和等于7)S
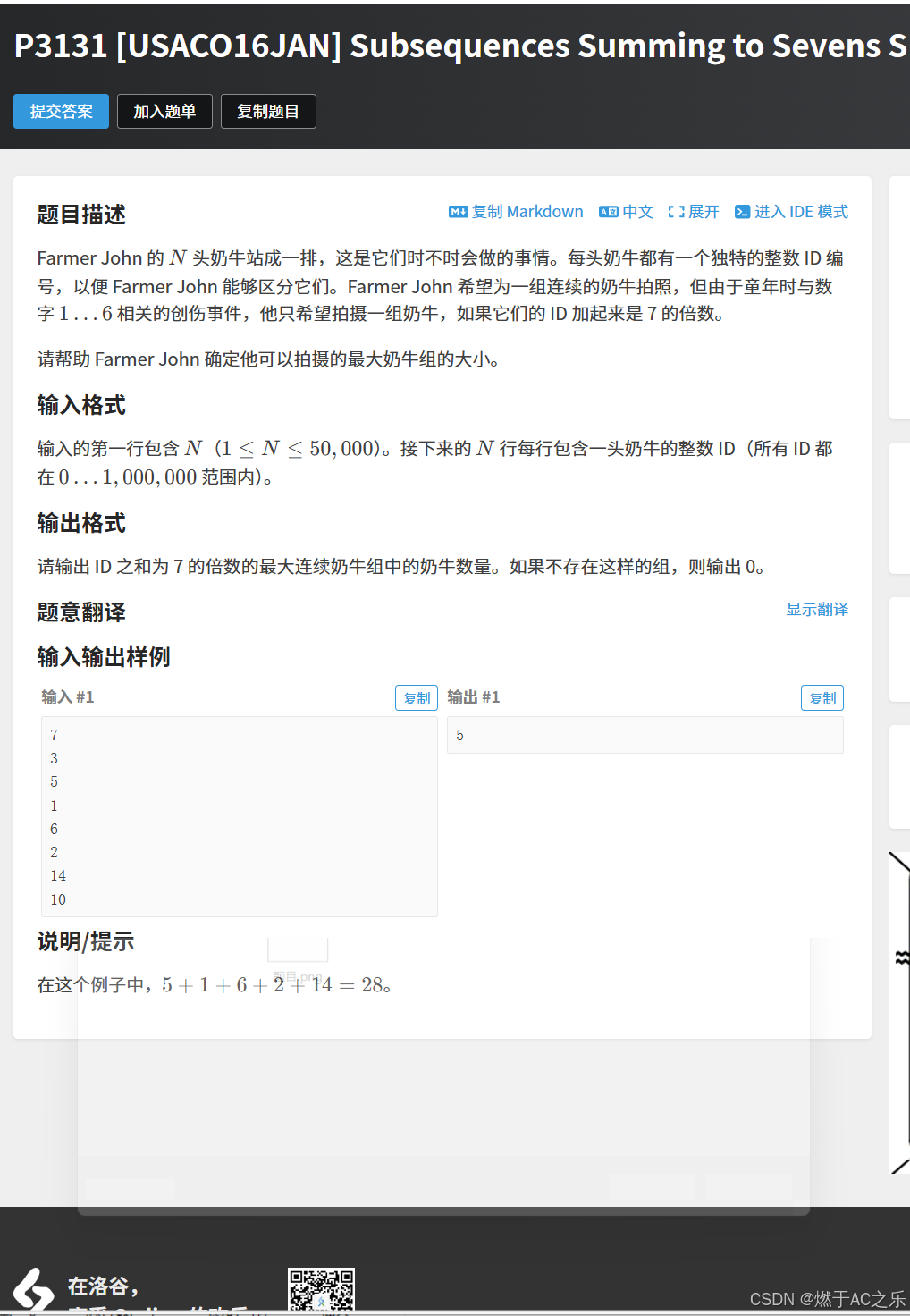
解法:前缀和 + 哈希表 + 同余
挑一个和为7的倍数的最长区间。
sum[i] -sum[j] = x,为了使得区间更长,j要尽可能靠左,区间长度ret = i - j
x % 7 = (sum[i] - sum[j]) % 7。
根据同余:(a - b) % m = a % m - b % m
那么,sum[i] % 7 = sum[j] % 7。
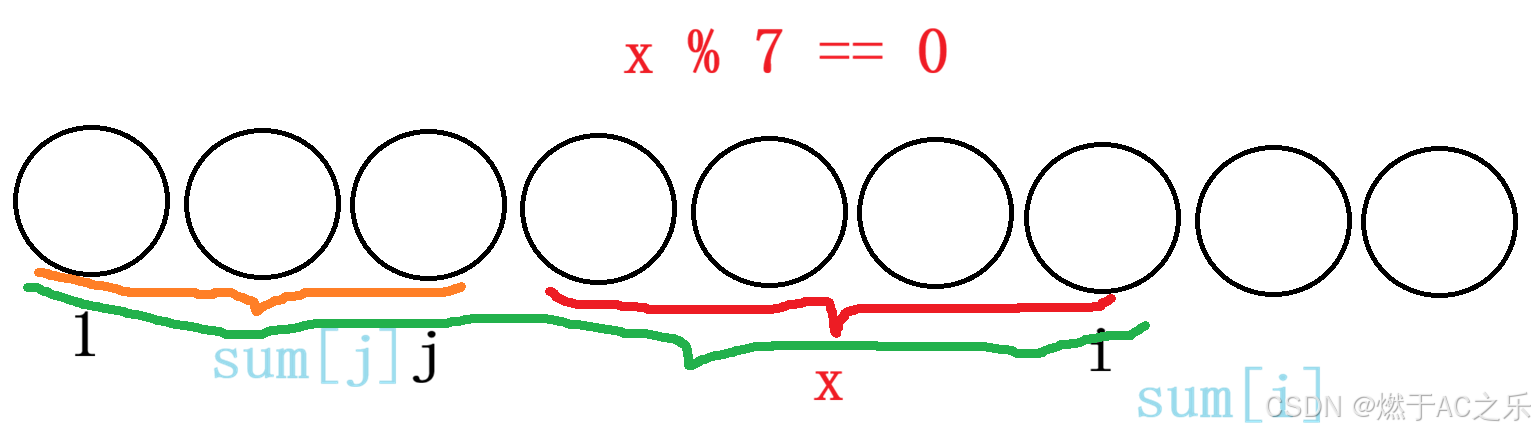
那么,这道题就转化为之前常做的题:找一个和为一个数(这里是7的倍数)的最长区间 ,前缀和 + 哈希表 用前缀和维护区间和的值 % 7,哈希表维护其对应的下标,<前缀和 % 7, 下标> ,mp[前缀和 % 7] = 下标 ,注意初始化:mp[0] = 0 。 当然,由于一个数 % 7 后的范围是 0~6 ,那么可以用数组 来存,id[n] = i, n : 0~6, 数组下标:前缀和 % 7,数组值:下标 。注意,初始化id[0] = 0 , 由于哈希表是一个一个存进去的,只用初始化mp[0] = 0,而数组有默认值,为了不让其产生影响,就用memset(id, -1, sizeof id),将为处理的标记为-1,用于后面的判断。
代码:
1.哈希表:
cpp
#include <iostream>
#include <unordered_map>
using namespace std;
int n;
unordered_map<int, int> mp; // <前缀和 % 7,下标>
int main()
{
mp[0] = 0;
cin >> n;
int sum = 0, ret = 0;
for(int i = 1; i <= n; i++)
{
int x; cin >> x;
sum = (sum + x) % 7;
if(mp.count(sum)) ret = max(ret, i - mp[sum]);
else mp[sum] = i;
}
cout << ret << endl;
return 0;
} 2.数组代替哈希表:
cpp
#include <iostream>
#include <cstring>
using namespace std;
const int N = 10;
int n;
//因为这里 % 7后结果为 0 ~ 6,可以用数组代替哈希表
int id[N]; //下标:%7之后为 0 ~ 6,值:对应的为第几个(下标)
int main()
{
cin >> n;
//初始化
memset(id, -1, sizeof id);
id[0] = 0;
int sum = 0, ret = 0;
for(int i = 1; i <= n; i++)
{
int x; cin >> x;
sum = (sum + x) % 7; //前缀和 % 7
if(id[sum] != -1) ret = max(ret, i - id[sum]); //存第一个,后面出现,长度为下标差值
else id[sum] = i;
}
cout << ret << endl;
return 0;
}6.图的遍历
题目: P3916 图的遍历
解法:正难则反-反图
从任意⼀点出发,去找能到达的最⼤结点,用dfs/bfs暴搜,n^2,(10 ^ 5) ^2, 最差情况(特殊图,要把所有结点都遍历一次)时间复杂度会超。正难则反-反图:但是如果对原图建⼀个反图,从节点编号最大的点出发,能走到的点都是原图能到达的点。这样走会使时间复杂度降低。
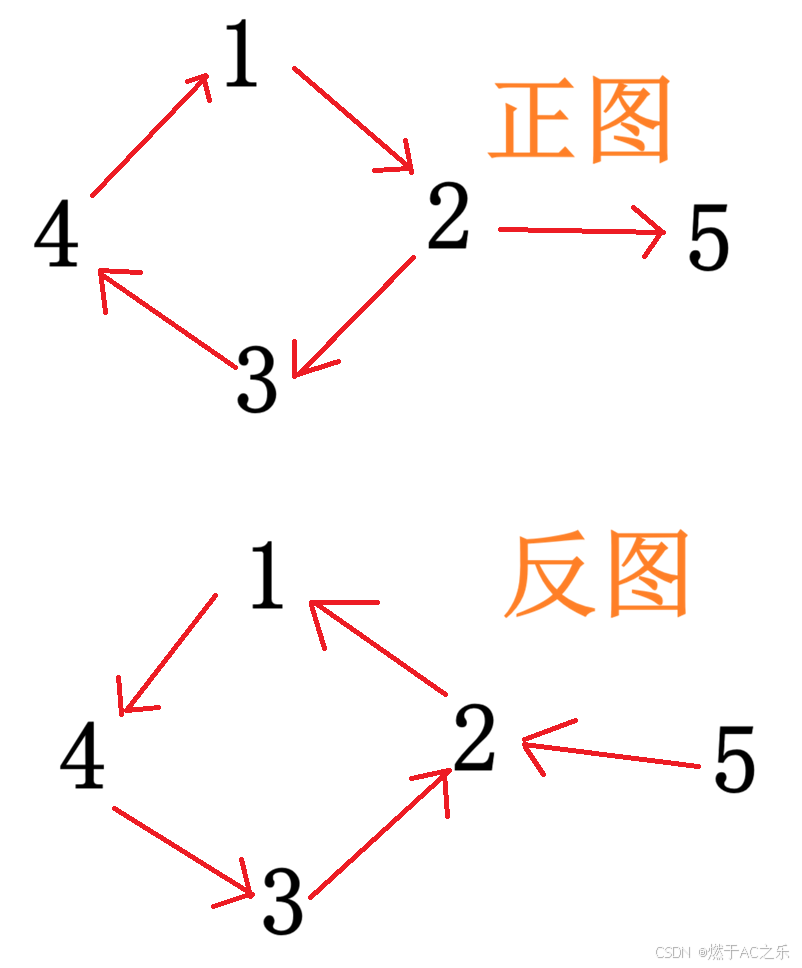
因此,建⼀个反图,按照节点编号从大到小dfs搜索⼀遍即可(这里从大到小还会起到一定的剪枝作用)。
代码:
cpp
#include <iostream>
#include <vector>
using namespace std;
const int N = 1e5 + 10;
int n, m;
vector<int> edges[N];
int ret[N]; //存结果,同时看是否走过
void dfs(int u, int r)
{
ret[u] = r;
for(auto v : edges[u])
{
if(ret[v]) continue;
dfs(v, r);
}
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= m; i++)
{
int a, b; cin >> a >> b;
//存反图
edges[b].push_back(a);
}
for(int i = n; i >= 1; i--) //从大到小遍历
{
if(ret[i]) continue; //走过
dfs(i, i); //从那个最终结点开始走
}
for(int i = 1; i <= n; i++)
{
cout << ret[i] << " ";
}
return 0;
}

加油!志同道合的人会看到同一片风景。
看到这里请点个赞 ,关注 ,如果觉得有用就收藏一下吧。后续还会持续更新的。 创作不易,还请多多支持!