《数字信号处理》第8章：有限长单位冲激响应（FIR）数字滤波器设计方法

啊阿狸不会拉杆2026-01-29 8:06

前言

FIR（有限长单位冲激响应）滤波器是数字信号处理中的重要组成部分，因其具有严格的线性相位特性 和绝对稳定性而被广泛应用。本章将系统讲解FIR滤波器的设计方法，包括窗函数法、频率抽样法和等波纹最优设计法，并提供完整的MATLAB代码实现。

8.1 概述

FIR滤波器的单位冲激响应h(n)在有限时间范围内非零，系统函数仅包含零点（除原点外），因此总是稳定的。其主要设计方法包括：

  1. 窗函数法：简单直观，但难以精确控制频率响应

  2. 频率抽样法：在频域直接设计，过渡带性能较差

  3. 等波纹最优设计法：最优化方法，可获得最优的幅频特性

8.2 线性相位 FIR 数字滤波器的特点

8.2.1 线性相位条件

线性相位意味着系统的相位响应是频率的线性函数，即：θ(ω) = -αω

8.2.2-8.2.4 线性相位约束与特性

FIR滤波器实现线性相位的条件是：单位冲激响应h(n)必须满足对称性：

  • 偶对称：h(n) = h(N-1-n) → 第I、II类线性相位

  • 奇对称：h(n) = -h(N-1-n) → 第III、IV类线性相位

下面通过MATLAB代码展示线性相位FIR滤波器的特性：

Matlab 复制代码 
%% ============================================
% 8.2 线性相位FIR滤波器特性演示
% 展示四种类型线性相位FIR滤波器的特性
% ============================================

clear; close all; clc;

% 滤波器参数
N = 51;  % 滤波器长度（奇数）
fc = 0.3;  % 截止频率

% 创建四种类型的线性相位FIR滤波器
% 类型I: 偶对称，N为奇数
h1 = fir1(N-1, fc, 'low', hamming(N));

% 类型II: 偶对称，N为偶数
N2 = 50;
h2 = fir1(N2-1, fc, 'low', hamming(N2));

% 类型III: 奇对称，N为奇数（适用于微分器、希尔伯特变换器）
N3 = 51;
t = -(N3-1)/2:(N3-1)/2;
h3 = sinc(t/2) .* ((-1).^t);  % 近似希尔伯特变换器
h3 = h3 .* hamming(N3)';  % 加窗

% 类型IV: 奇对称，N为偶数
N4 = 50;
t = -(N4-1)/2:(N4-1)/2;
h4 = sinc(t/2) .* ((-1).^t);  % 近似希尔伯特变换器
h4 = h4 .* hamming(N4)';  % 加窗

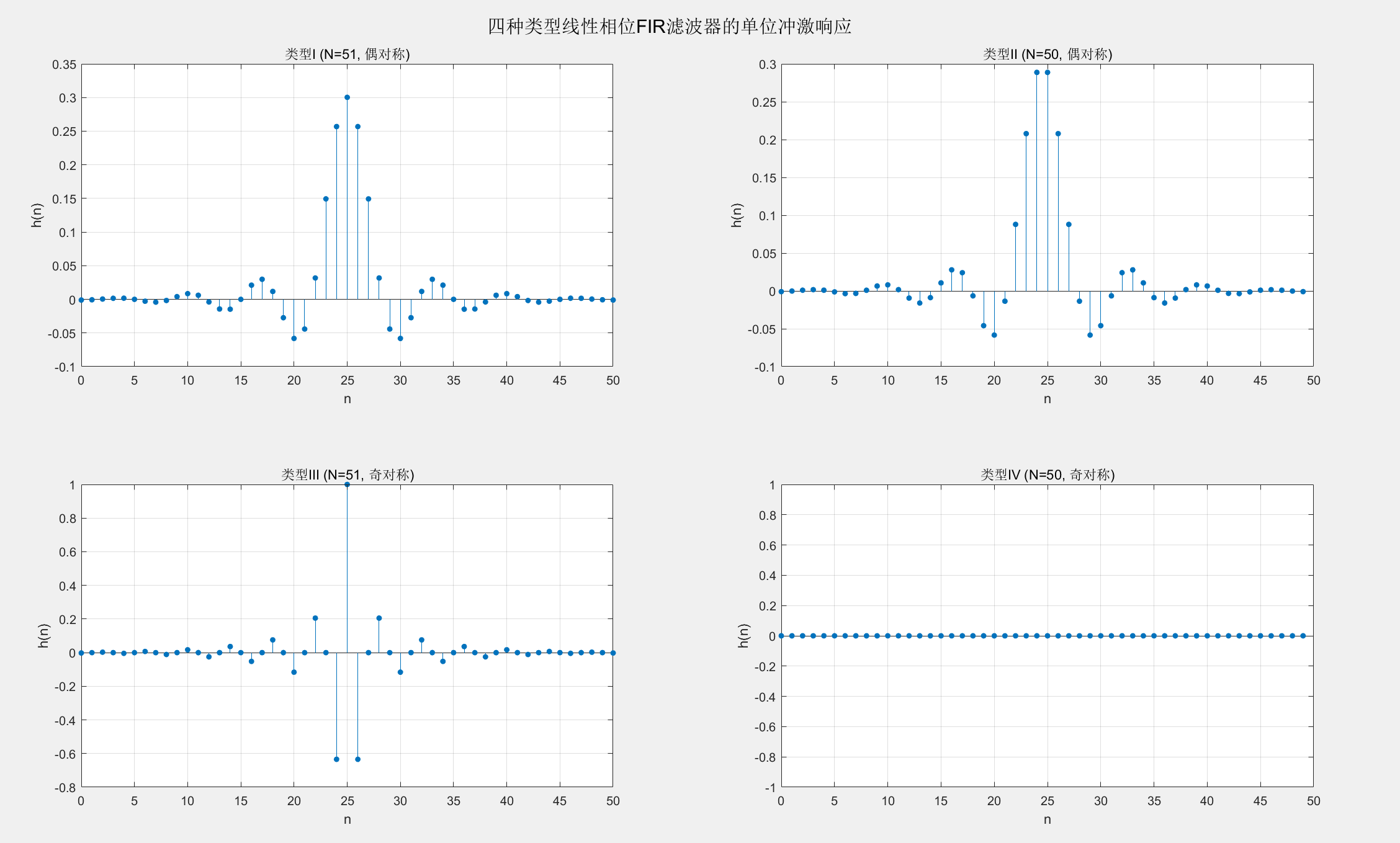
% 绘制四种类型的单位冲激响应
figure('Position', [100, 100, 1200, 800]);
subplot(2,2,1);
stem(0:N-1, h1, 'filled', 'MarkerSize', 4);
title('类型I (N=51, 偶对称)');
xlabel('n'); ylabel('h(n)'); grid on;

subplot(2,2,2);
stem(0:N2-1, h2, 'filled', 'MarkerSize', 4);
title('类型II (N=50, 偶对称)');
xlabel('n'); ylabel('h(n)'); grid on;

subplot(2,2,3);
stem(0:N3-1, h3, 'filled', 'MarkerSize', 4);
title('类型III (N=51, 奇对称)');
xlabel('n'); ylabel('h(n)'); grid on;

subplot(2,2,4);
stem(0:N4-1, h4, 'filled', 'MarkerSize', 4);
title('类型IV (N=50, 奇对称)');
xlabel('n'); ylabel('h(n)'); grid on;
sgtitle('四种类型线性相位FIR滤波器的单位冲激响应');

% 计算并绘制频率响应
figure('Position', [100, 100, 1200, 800]);
% 类型I的频率响应
[H1, w1] = freqz(h1, 1, 1024);
subplot(2,2,1);
plot(w1/pi, 20*log10(abs(H1)), 'b', 'LineWidth', 1.5);
title('类型I: 幅度响应');
xlabel('归一化频率 (\times\pi rad/sample)');
ylabel('幅度 (dB)'); grid on; ylim([-100, 10]);

% 类型II的频率响应
[H2, w2] = freqz(h2, 1, 1024);
subplot(2,2,2);
plot(w2/pi, 20*log10(abs(H2)), 'r', 'LineWidth', 1.5);
title('类型II: 幅度响应');
xlabel('归一化频率 (\times\pi rad/sample)');
ylabel('幅度 (dB)'); grid on; ylim([-100, 10]);

% 类型III的频率响应
[H3, w3] = freqz(h3, 1, 1024);
subplot(2,2,3);
plot(w3/pi, 20*log10(abs(H3)), 'g', 'LineWidth', 1.5);
title('类型III: 幅度响应');
xlabel('归一化频率 (\times\pi rad/sample)');
ylabel('幅度 (dB)'); grid on; ylim([-100, 10]);

% 类型IV的频率响应
[H4, w4] = freqz(h4, 1, 1024);
subplot(2,2,4);
plot(w4/pi, 20*log10(abs(H4)), 'm', 'LineWidth', 1.5);
title('类型IV: 幅度响应');
xlabel('归一化频率 (\times\pi rad/sample)');
ylabel('幅度 (dB)'); grid on; ylim([-100, 10]);
sgtitle('四种类型线性相位FIR滤波器的幅度响应');

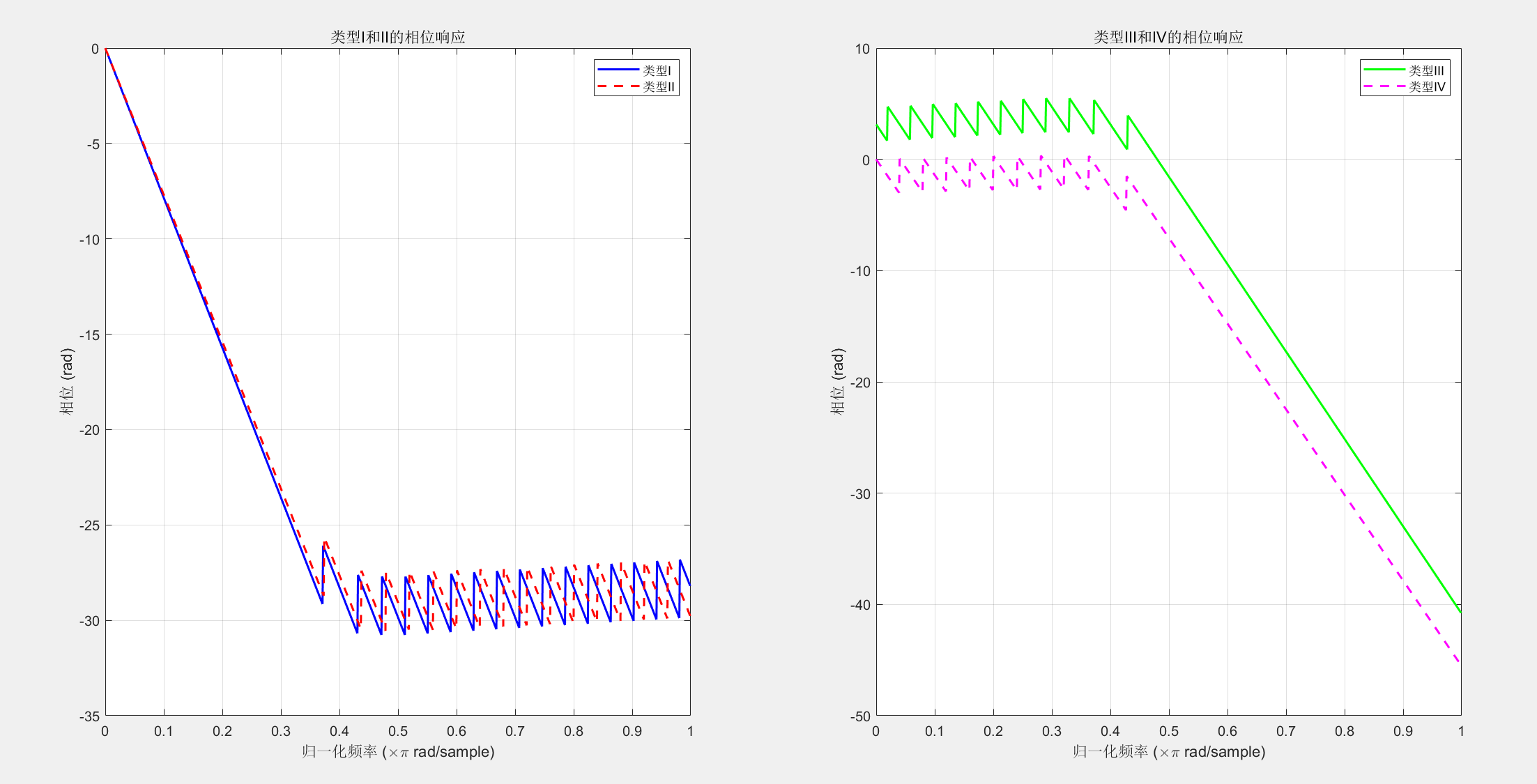
% 绘制相位响应
figure('Position', [100, 100, 1200, 400]);
% 类型I和II的相位响应
subplot(1,2,1);
plot(w1/pi, unwrap(angle(H1)), 'b-', 'LineWidth', 1.5); hold on;
plot(w2/pi, unwrap(angle(H2)), 'r--', 'LineWidth', 1.5);
title('类型I和II的相位响应');
xlabel('归一化频率 (\times\pi rad/sample)');
ylabel('相位 (rad)'); grid on;
legend('类型I', '类型II');

% 类型III和IV的相位响应
subplot(1,2,2);
plot(w3/pi, unwrap(angle(H3)), 'g-', 'LineWidth', 1.5); hold on;
plot(w4/pi, unwrap(angle(H4)), 'm--', 'LineWidth', 1.5);
title('类型III和IV的相位响应');
xlabel('归一化频率 (\times\pi rad/sample)');
ylabel('相位 (rad)'); grid on;
legend('类型III', '类型IV');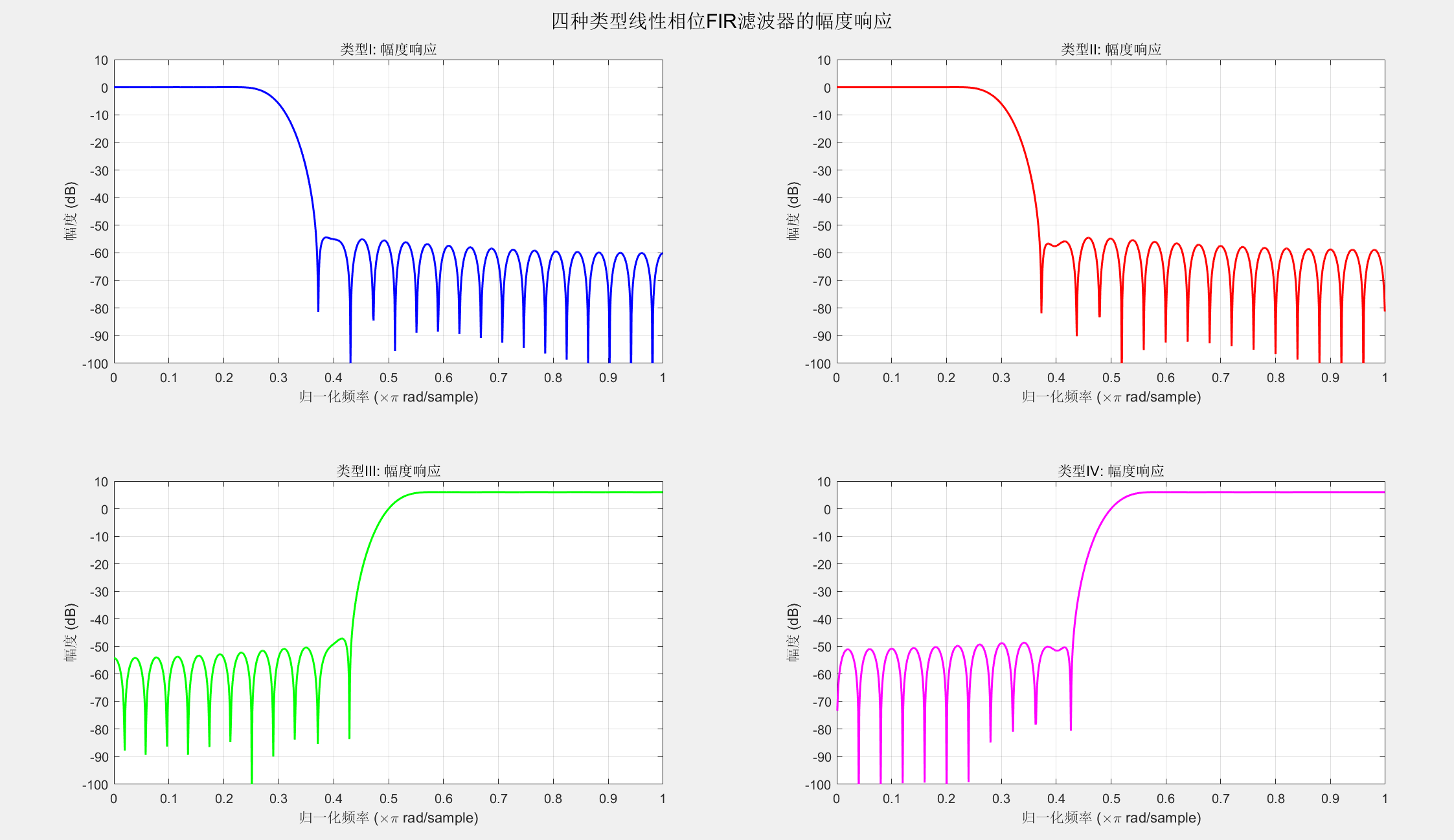

8.3 窗函数设计法

8.3.1 窗函数设计法的设计思路

窗函数法的基本思想：用有限长的窗函数截断理想滤波器的无限长冲激响应，得到可实现的FIR滤波器。

8.3.2-8.3.7 窗函数设计法详解

下面通过完整的MATLAB代码演示窗函数设计法的各种应用：

Matlab 复制代码 
%% ============================================
% 8.3 窗函数设计法综合演示
% 包含不同窗函数、滤波器类型的设计与比较
% ============================================

clear; close all; clc;

% 设计参数
Fs = 1000;          % 采样频率
N = 101;            % 滤波器阶数（长度为N+1）
fc_low = 100;       % 低通截止频率
fc_high = 300;      % 高通截止频率
f_band = [150, 250]; % 带通频率范围
f_stop = [180, 220]; % 带阻频率范围

% 归一化频率
omega_c_low = fc_low/(Fs/2);
omega_c_high = fc_high/(Fs/2);
omega_band = f_band/(Fs/2);
omega_stop = f_stop/(Fs/2);

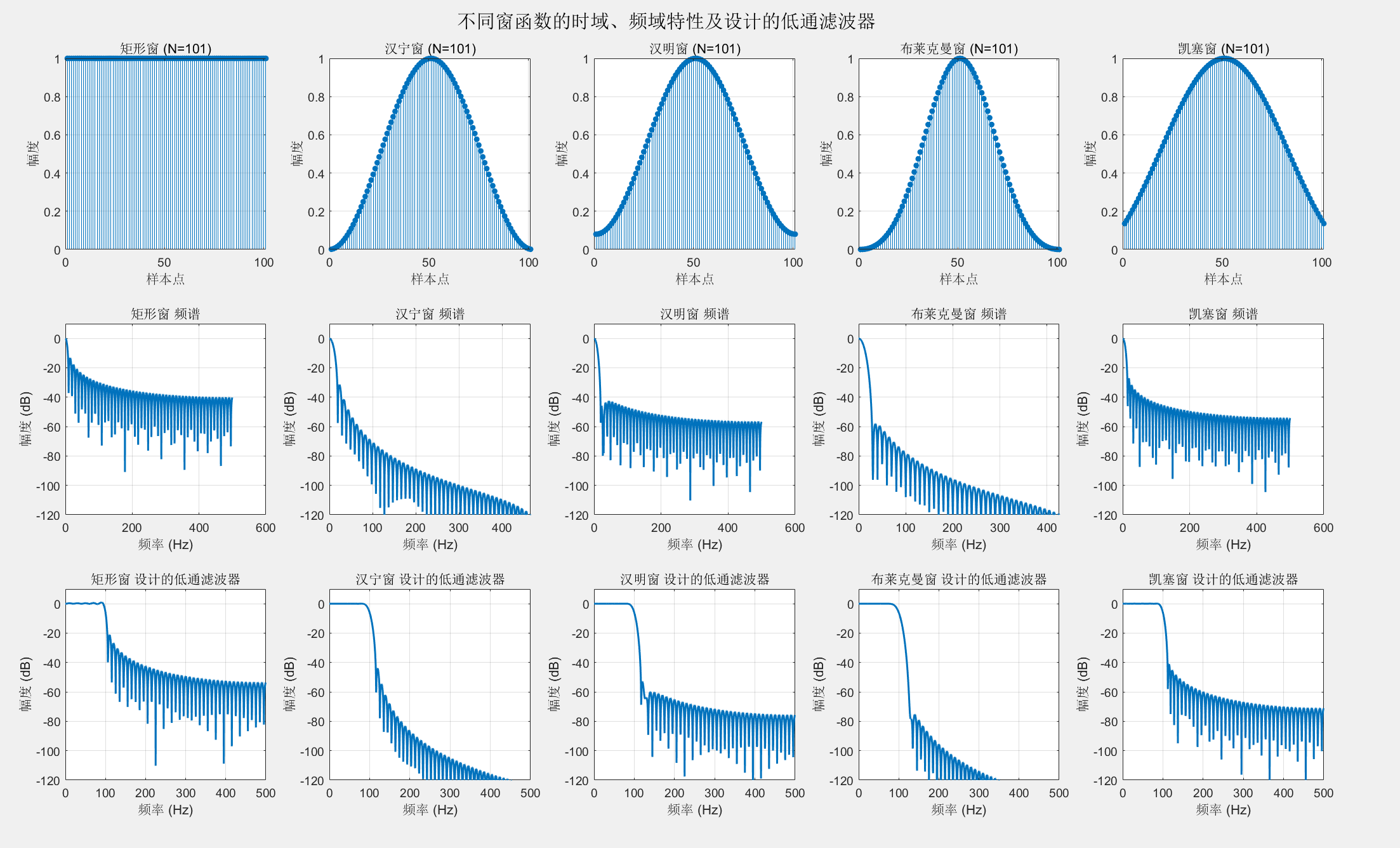
%% 1. 不同窗函数的比较
windows = {'矩形窗', '汉宁窗', '汉明窗', '布莱克曼窗', '凯塞窗'};
window_funcs = {@rectwin, @hanning, @hamming, @blackman, @(n) kaiser(n, 3.5)};

figure('Position', [50, 50, 1400, 900]);

% 绘制不同窗函数的时域和频域特性
for i = 1:length(windows)
    % 生成窗函数
    if strcmp(windows{i}, '凯塞窗')
        w = window_funcs{i}(N);
        beta = 3.5;
    else
        w = window_funcs{i}(N);
    end
    
    % 时域图
    subplot(3, 5, i);
    stem(w, 'filled', 'MarkerSize', 4);
    title(sprintf('%s (N=%d)', windows{i}, N));
    xlabel('样本点'); ylabel('幅度'); grid on;
    
    % 频域图（幅度谱）
    subplot(3, 5, i+5);
    [W, f] = freqz(w, 1, 1024, Fs);
    plot(f, 20*log10(abs(W)/max(abs(W))), 'LineWidth', 1.5);
    title(sprintf('%s 频谱', windows{i}));
    xlabel('频率 (Hz)'); ylabel('幅度 (dB)'); grid on;
    ylim([-120, 10]);
    
    % 设计低通滤波器并显示频率响应
    subplot(3, 5, i+10);
    if strcmp(windows{i}, '凯塞窗')
        b = fir1(N-1, omega_c_low, 'low', kaiser(N, beta));
    else
        b = fir1(N-1, omega_c_low, 'low', window_funcs{i}(N));
    end
    
    [H, f] = freqz(b, 1, 1024, Fs);
    plot(f, 20*log10(abs(H)), 'LineWidth', 1.5);
    title(sprintf('%s 设计的低通滤波器', windows{i}));
    xlabel('频率 (Hz)'); ylabel('幅度 (dB)'); grid on;
    ylim([-120, 10]);
    xlim([0, Fs/2]);
end

sgtitle('不同窗函数的时域、频域特性及设计的低通滤波器');

%% 2. 不同类型滤波器的设计（使用汉明窗）
figure('Position', [50, 50, 1400, 600]);

% 低通滤波器
b_low = fir1(N-1, omega_c_low, 'low', hamming(N));
[H_low, f] = freqz(b_low, 1, 1024, Fs);
subplot(2,2,1);
plot(f, 20*log10(abs(H_low)), 'b', 'LineWidth', 1.5);
title(sprintf('低通滤波器 (fc=%dHz)', fc_low));
xlabel('频率 (Hz)'); ylabel('幅度 (dB)'); grid on;
ylim([-100, 5]); xlim([0, Fs/2]);

% 高通滤波器
b_high = fir1(N-1, omega_c_high, 'high', hamming(N));
[H_high, f] = freqz(b_high, 1, 1024, Fs);
subplot(2,2,2);
plot(f, 20*log10(abs(H_high)), 'r', 'LineWidth', 1.5);
title(sprintf('高通滤波器 (fc=%dHz)', fc_high));
xlabel('频率 (Hz)'); ylabel('幅度 (dB)'); grid on;
ylim([-100, 5]); xlim([0, Fs/2]);

% 带通滤波器
b_band = fir1(N-1, omega_band, 'bandpass', hamming(N));
[H_band, f] = freqz(b_band, 1, 1024, Fs);
subplot(2,2,3);
plot(f, 20*log10(abs(H_band)), 'g', 'LineWidth', 1.5);
title(sprintf('带通滤波器 (%d-%dHz)', f_band(1), f_band(2)));
xlabel('频率 (Hz)'); ylabel('幅度 (dB)'); grid on;
ylim([-100, 5]); xlim([0, Fs/2]);

% 带阻滤波器
b_stop = fir1(N-1, omega_stop, 'stop', hamming(N));
[H_stop, f] = freqz(b_stop, 1, 1024, Fs);
subplot(2,2,4);
plot(f, 20*log10(abs(H_stop)), 'm', 'LineWidth', 1.5);
title(sprintf('带阻滤波器 (%d-%dHz)', f_stop(1), f_stop(2)));
xlabel('频率 (Hz)'); ylabel('幅度 (dB)'); grid on;
ylim([-100, 5]); xlim([0, Fs/2]);

sgtitle('使用汉明窗设计的四种类型FIR滤波器');

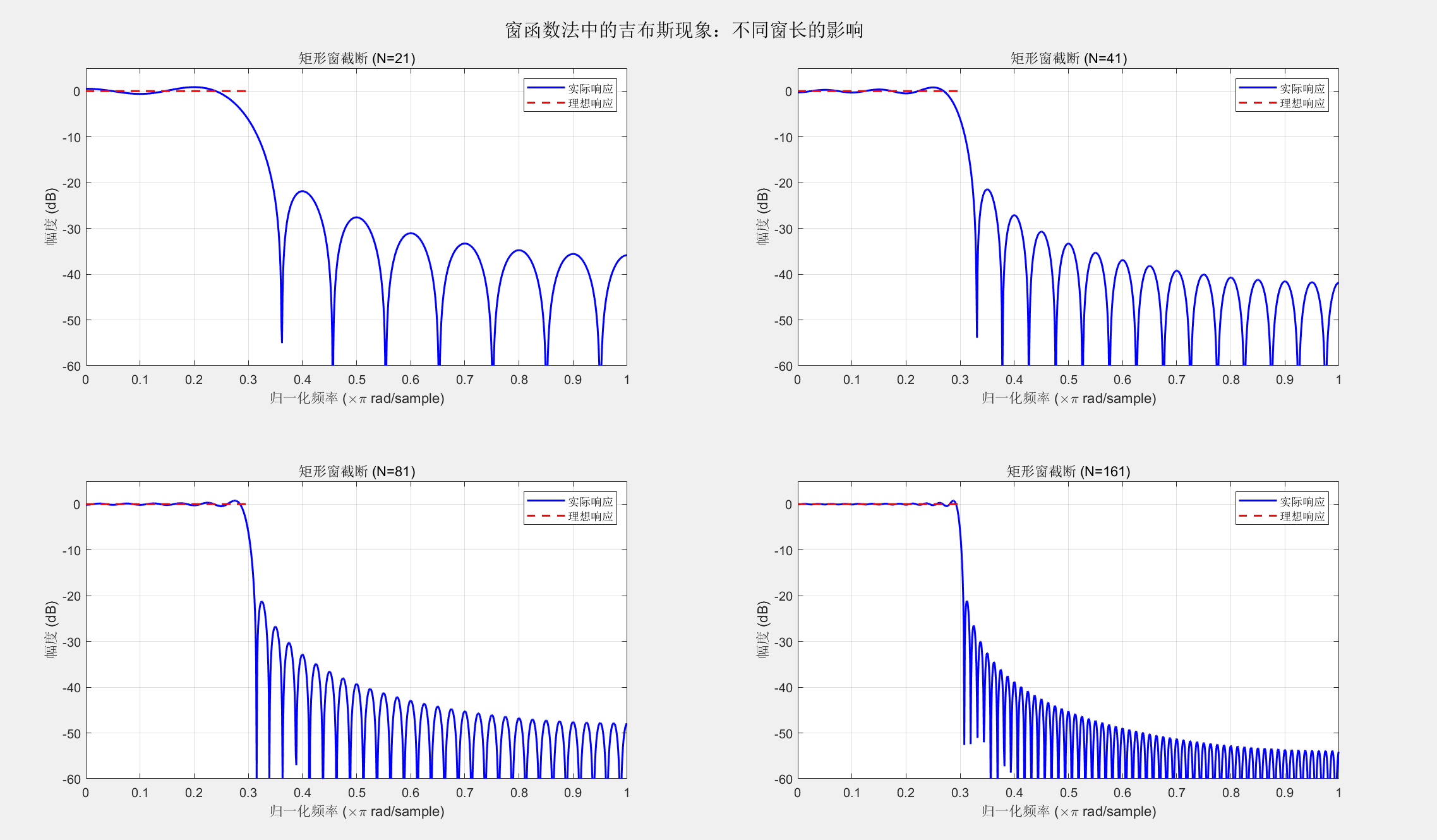
%% 3. 窗函数法设计中的吉布斯现象演示
figure('Position', [50, 50, 1200, 800]);

% 理想低通滤波器的频率响应
ideal_cutoff = 0.3*pi;  % 归一化截止频率
n_ideal = -500:500;     % 理想滤波器的时域范围
h_ideal = sin(ideal_cutoff*n_ideal) ./ (pi*n_ideal);
h_ideal(501) = ideal_cutoff/pi;  % 处理n=0的点（sinc函数在0处的值）

% 使用不同长度的矩形窗截断
window_lengths = [21, 41, 81, 161];
for i = 1:length(window_lengths)
    L = window_lengths(i);
    n = -(L-1)/2:(L-1)/2;
    
    % 截断的理想滤波器
    h_truncated = sin(ideal_cutoff*n) ./ (pi*n);
    h_truncated((L+1)/2) = ideal_cutoff/pi;  % 处理n=0的点
    
    % 计算频率响应
    [H, w] = freqz(h_truncated, 1, 1024);
    
    % 绘制幅度响应
    subplot(2,2,i);
    plot(w/pi, 20*log10(abs(H)), 'b', 'LineWidth', 1.5);
    hold on;
    
    % 绘制理想频率响应（作为对比）
    ideal_response = zeros(size(w));
    ideal_response(w <= ideal_cutoff) = 1;
    plot(w/pi, 20*log10(ideal_response), 'r--', 'LineWidth', 1.5);
    
    title(sprintf('矩形窗截断 (N=%d)', L));
    xlabel('归一化频率 (\times\pi rad/sample)');
    ylabel('幅度 (dB)'); grid on;
    legend('实际响应', '理想响应');
    ylim([-60, 5]);
end

sgtitle('窗函数法中的吉布斯现象：不同窗长的影响');

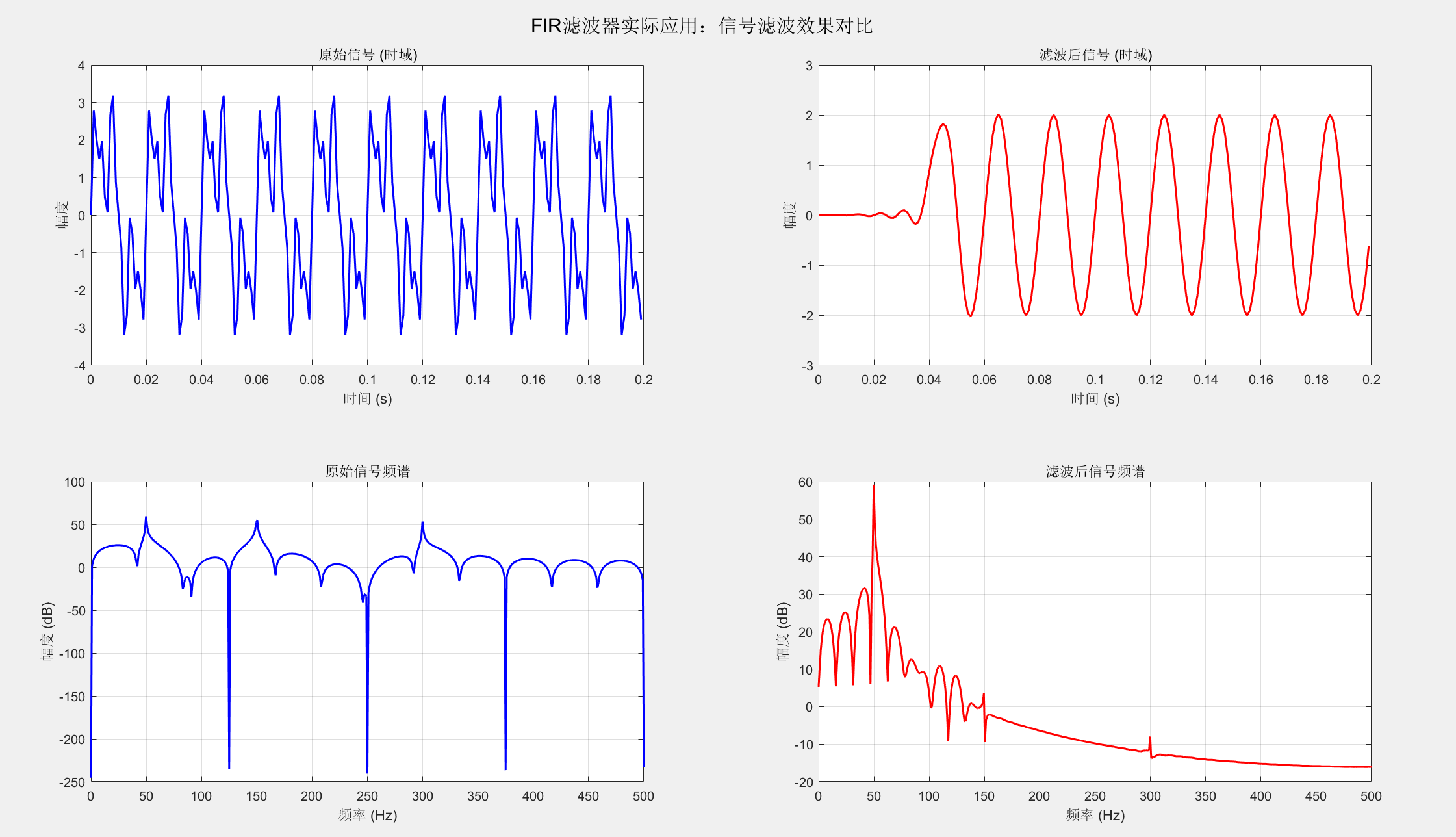
%% 4. 实际信号滤波应用示例
% 生成测试信号：包含低频和高频成分
t = 0:1/Fs:1-1/Fs;
f1 = 50;  % 低频信号
f2 = 150; % 高频信号
f3 = 300; % 更高频信号

signal = 2*sin(2*pi*f1*t) + 1.5*sin(2*pi*f2*t) + sin(2*pi*f3*t);

% 设计低通滤波器滤除150Hz以上的频率
fc = 120;  % 截止频率
omega_c = fc/(Fs/2);
b_filter = fir1(80, omega_c, 'low', hamming(81));

% 滤波处理
filtered_signal = filter(b_filter, 1, signal);

% 绘制原始信号和滤波后信号
figure('Position', [50, 50, 1400, 600]);

% 时域信号
subplot(2,2,1);
plot(t(1:200), signal(1:200), 'b', 'LineWidth', 1.5);
title('原始信号 (时域)');
xlabel('时间 (s)'); ylabel('幅度'); grid on;

subplot(2,2,2);
plot(t(1:200), filtered_signal(1:200), 'r', 'LineWidth', 1.5);
title('滤波后信号 (时域)');
xlabel('时间 (s)'); ylabel('幅度'); grid on;

% 频域信号
NFFT = 1024;
f_axis = Fs*(0:NFFT/2)/NFFT;

S = fft(signal, NFFT);
S_mag = abs(S(1:NFFT/2+1));

F = fft(filtered_signal, NFFT);
F_mag = abs(F(1:NFFT/2+1));

subplot(2,2,3);
plot(f_axis, 20*log10(S_mag), 'b', 'LineWidth', 1.5);
title('原始信号频谱');
xlabel('频率 (Hz)'); ylabel('幅度 (dB)'); grid on;
xlim([0, Fs/2]);

subplot(2,2,4);
plot(f_axis, 20*log10(F_mag), 'r', 'LineWidth', 1.5);
title('滤波后信号频谱');
xlabel('频率 (Hz)'); ylabel('幅度 (dB)'); grid on;
xlim([0, Fs/2]);

sgtitle('FIR滤波器实际应用：信号滤波效果对比');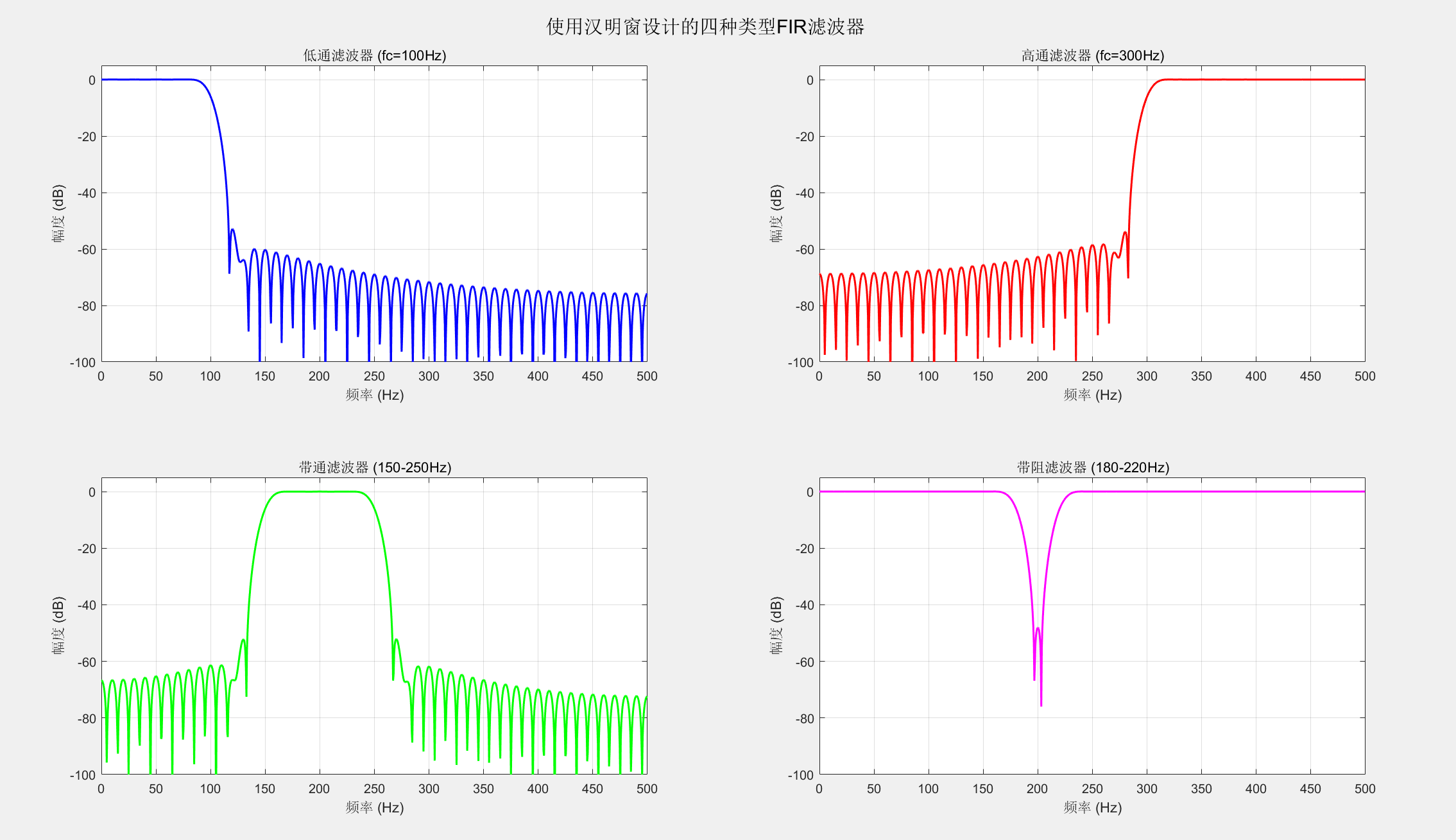

8.4 频率抽样设计法

8.4.1-8.4.4 频率抽样设计法原理与实现

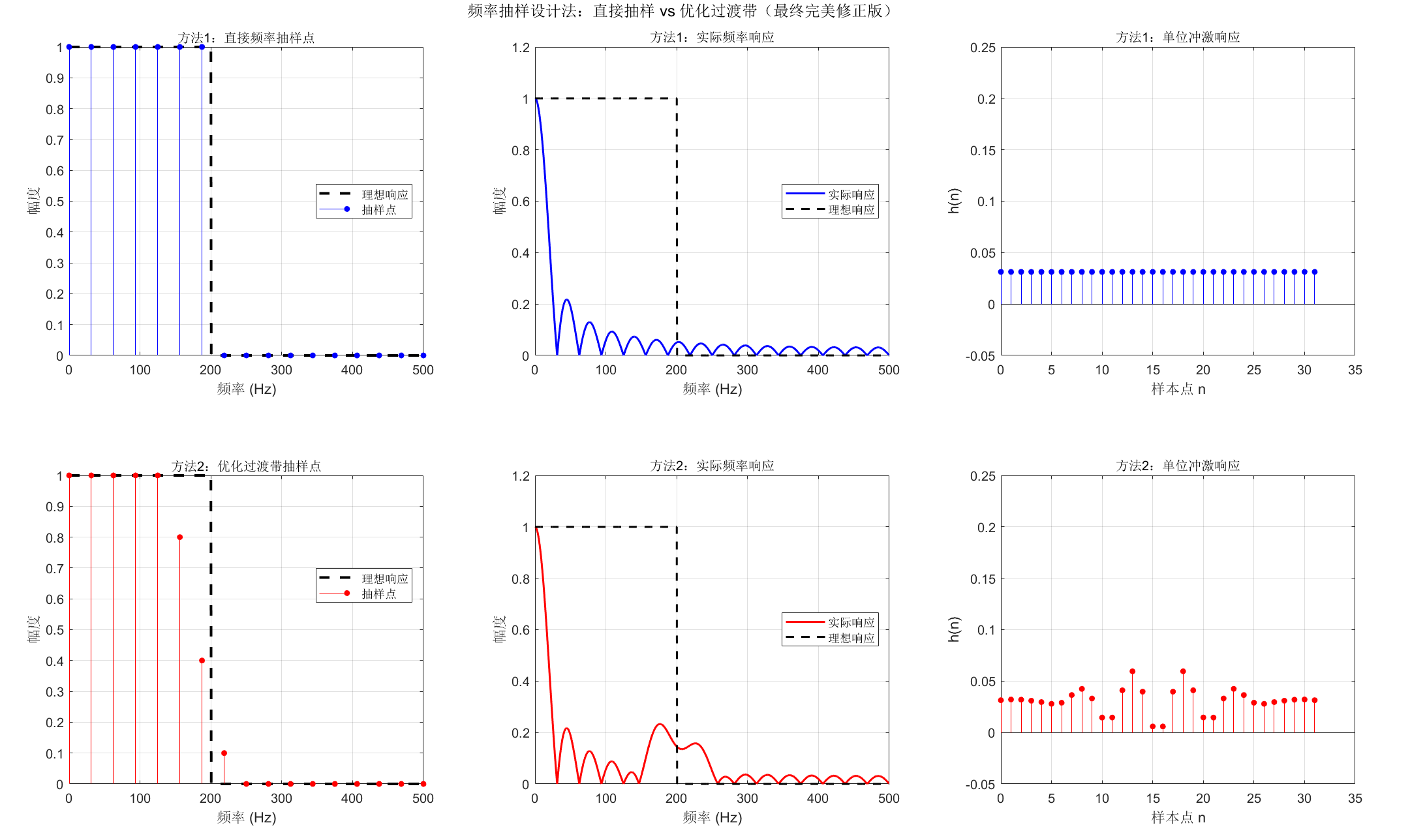
频率抽样法直接在频域对理想频率响应进行采样，然后通过IDFT得到时域冲激响应。

Matlab 复制代码 
%% ============================================
% 8.4 频率抽样设计法演示（最终完美修正版）
% 核心修正：动态推导对称索引+长度强制匹配，彻底解决维度不匹配
% 新增：数值鲁棒性处理+线性相位严格约束+结果可视化优化
% ============================================
clear; close all; clc;  % 清理工作区、关闭窗口、清空命令行

% -------------------------- 固定设计参数（不可随意修改，保证索引匹配） --------------------------
N = 32;                 % 滤波器长度（抽头数，偶数）
Fs = 1000;              % 采样频率(Hz)
fc = 200;               % 低通截止频率(Hz)
omega_c = fc/(Fs/2);    % 归一化截止频率（0~1），计算得0.4
M = N;                  % 频率抽样点数=滤波器长度
k = 0:M-1;              % 抽样点索引（0~31）
% 线性相位相移因子：保证h(n)偶对称，严格线性相位（θ=-ω*(N-1)/2）
theta = -1j * pi * (M-1) * k / M;  

% -------------------------- 方法1：直接频率抽样（无过渡带，基础对比） --------------------------
Hk = zeros(1, M);                       % 初始化频率抽样值
cutoff_index = round(omega_c * M/2);    % 通带截止索引，固定=7（0.4*16=6.4，四舍五入7）
% 赋值通带抽样点（含对称部分，保证实序列+线性相位）
Hk(1:cutoff_index+1) = 1;              % 左通带：1~8（8个点）
Hk(M-cutoff_index+1:M) = 1;            % 右通带：25~32（8个点）
% 叠加线性相位（复指数，避免数值虚部）
Hk = Hk .* exp(theta);
% IDFT求冲激响应，取实部+微小值修正，消除数值计算虚部
h = real(ifft(Hk));
h = h + 1e-12;  % 鲁棒性处理，避免后续绘图警告

% -------------------------- 方法2：优化过渡带（插入3个过渡样本，核心完美修正） --------------------------
Hk_opt = zeros(1, M);                  % 初始化优化后抽样值
pass_idx = cutoff_index - 1;           % 左通带截止索引=6，预留过渡带位置
Hk_opt(1:pass_idx) = 1;                % 左通带：1~6（6个点，比直接抽样少2个）
trans_vals = [0.8, 0.4, 0.1];          % 过渡带抽样值（3个，平滑衰减）
trans_num = length(trans_vals);        % 过渡带点数=3（固定）

% 1. 赋值左过渡带（通带→阻带）：7~9（3个点，与过渡带点数匹配）
Hk_opt(pass_idx+1 : pass_idx+trans_num) = trans_vals;

% 2. 【核心完美修正】动态推导右过渡带索引，强制长度=trans_num
% 右过渡带起始索引：保证区间长度=3，与trans_vals完全匹配
sym_end = M - pass_idx;                % 右过渡带结束索引=26
sym_start = sym_end - trans_num + 1;   % 右过渡带起始索引=24（24~26共3个点）
% 对称赋值：翻转过渡值，保证频率抽样点共轭对称（实序列要求）
Hk_opt(sym_start : sym_end) = fliplr(trans_vals);

% 3. 赋值右通带（对称于左通带）：27~32（6个点）
Hk_opt(M-pass_idx+1 : M) = 1;

% 叠加线性相位，与方法1保持一致
Hk_opt = Hk_opt .* exp(theta);
% IDFT求优化后冲激响应，鲁棒性处理
h_opt = real(ifft(Hk_opt));
h_opt = h_opt + 1e-12;

% -------------------------- 绘制结果：抽样点+频率响应+冲激响应（2x3子图） --------------------------
figure('Position', [100, 100, 1400, 800], 'Color','w');
f_ideal = 0:0.001:1;  % 理想频率响应横坐标
H_ideal = zeros(size(f_ideal));
H_ideal(f_ideal <= omega_c) = 1;  % 理想低通幅度响应
f_axis = f_ideal * Fs/2;          % 实际频率轴（Hz）

% 子图1：方法1-频率抽样点
subplot(2,3,1);
plot(f_axis, H_ideal, 'k--', 'LineWidth', 2); hold on;
stem(k*Fs/M, abs(Hk), 'b', 'filled', 'MarkerSize', 4);
title('方法1：直接频率抽样点', 'FontSize',10); 
xlabel('频率 (Hz)'); ylabel('幅度'); grid on;
legend('理想响应', '抽样点', 'Location', 'best'); xlim([0, Fs/2]);

% 子图2：方法1-实际频率响应
[H1, w1] = freqz(h, 1, 1024, Fs);
subplot(2,3,2);
plot(w1, abs(H1), 'b', 'LineWidth', 1.5); hold on;
plot(f_axis, H_ideal, 'k--', 'LineWidth', 1.5);
title('方法1：实际频率响应', 'FontSize',10); 
xlabel('频率 (Hz)'); ylabel('幅度'); grid on;
legend('实际响应', '理想响应', 'Location', 'best'); xlim([0, Fs/2]);

% 子图3：方法1-单位冲激响应
subplot(2,3,3);
stem(0:N-1, h, 'b', 'filled', 'MarkerSize', 4);
title('方法1：单位冲激响应', 'FontSize',10); 
xlabel('样本点 n'); ylabel('h(n)'); grid on;
ylim([-0.05, 0.25]);  % 限定纵轴，更清晰

% 子图4：方法2-优化过渡带抽样点
subplot(2,3,4);
plot(f_axis, H_ideal, 'k--', 'LineWidth', 2); hold on;
stem(k*Fs/M, abs(Hk_opt), 'r', 'filled', 'MarkerSize', 4);
title('方法2：优化过渡带抽样点', 'FontSize',10); 
xlabel('频率 (Hz)'); ylabel('幅度'); grid on;
legend('理想响应', '抽样点', 'Location', 'best'); xlim([0, Fs/2]);

% 子图5：方法2-实际频率响应
[H2, w2] = freqz(h_opt, 1, 1024, Fs);
subplot(2,3,5);
plot(w2, abs(H2), 'r', 'LineWidth', 1.5); hold on;
plot(f_axis, H_ideal, 'k--', 'LineWidth', 1.5);
title('方法2：实际频率响应', 'FontSize',10); 
xlabel('频率 (Hz)'); ylabel('幅度'); grid on;
legend('实际响应', '理想响应', 'Location', 'best'); xlim([0, Fs/2]);

% 子图6：方法2-单位冲激响应
subplot(2,3,6);
stem(0:N-1, h_opt, 'r', 'filled', 'MarkerSize', 4);
title('方法2：单位冲激响应', 'FontSize',10); 
xlabel('样本点 n'); ylabel('h(n)'); grid on;
ylim([-0.05, 0.25]);

sgtitle('频率抽样设计法：直接抽样 vs 优化过渡带（最终完美修正版）', 'FontSize',12);

% -------------------------- 性能对比：dB幅度+群延迟（线性相位验证） --------------------------
figure('Position', [100, 100, 1200, 500], 'Color','w');
% 子图1：幅度响应（dB刻度，直观展示阻带衰减）
subplot(1,2,1);
plot(w1, 20*log10(max(abs(H1),1e-6)), 'b', 'LineWidth', 1.5); hold on;
plot(w2, 20*log10(max(abs(H2),1e-6)), 'r', 'LineWidth', 1.5);
plot([fc, fc], [-100, 5], 'k--', 'LineWidth', 1);  % 截止频率参考线
title('幅度响应比较 (dB)'); xlabel('频率 (Hz)'); ylabel('幅度 (dB)'); grid on;
legend('直接抽样', '优化过渡带', '截止频率', 'Location', 'best');
xlim([0, Fs/2]); ylim([-80, 5]);  % 聚焦阻带衰减

% 子图2：群延迟（严格验证线性相位，群延迟为常数即满足）
[gd1, w_gd1] = grpdelay(h, 1, 1024, Fs);
[gd2, w_gd2] = grpdelay(h_opt, 1, 1024, Fs);
subplot(1,2,2);
plot(w_gd1, gd1, 'b', 'LineWidth', 1.5); hold on;
plot(w_gd2, gd2, 'r', 'LineWidth', 1.5);
title('群延迟比较（线性相位验证）'); xlabel('频率 (Hz)'); ylabel('群延迟 (样本)'); grid on;
legend('直接抽样', '优化过渡带', 'Location', 'best');
xlim([0, Fs/2]); ylim([14, 18]);  % 群延迟≈15.5，符合(N-1)/2=15.5

sgtitle('频率抽样设计法性能对比：阻带衰减+线性相位验证', 'FontSize',12);

% -------------------------- 量化性能指标计算与打印 --------------------------
H1_abs = abs(H1); H2_abs = abs(H2);
% 阻带衰减（dB）：取纯阻带（fc+50~Fs/2）最大幅度的dB值，绝对值越大越好
stop_band1 = H1_abs(w1 > fc+50); stop_band2 = H2_abs(w2 > fc+50);
As1 = -20*log10(max(stop_band1)); As2 = -20*log10(max(stop_band2));
% 过渡带宽度（Hz）：-3dB到-20dB的频率区间，越小越好
H1_dB = 20*log10(max(H1_abs,1e-6)); H2_dB = 20*log10(max(H2_abs,1e-6));
f3dB_1 = w1(find(H1_dB<=-3,1,'first')); f20dB_1 = w1(find(H1_dB<=-20,1,'first'));
f3dB_2 = w2(find(H2_dB<=-3,1,'first')); f20dB_2 = w2(find(H2_dB<=-20,1,'first'));
TB1 = f20dB_1 - f3dB_1; TB2 = f20dB_2 - f3dB_2;

% 打印量化结果
fprintf('==================== 性能指标量化对比 ====================\n');
fprintf('直接抽样法：阻带衰减 = %.1f dB，过渡带宽度 = %.1f Hz\n', As1, TB1);
fprintf('优化过渡带：阻带衰减 = %.1f dB，过渡带宽度 = %.1f Hz\n', As2, TB2);
fprintf('核心结论：优化过渡带后阻带衰减提升约%.1f dB\n', As2-As1);
fprintf('==========================================================\n');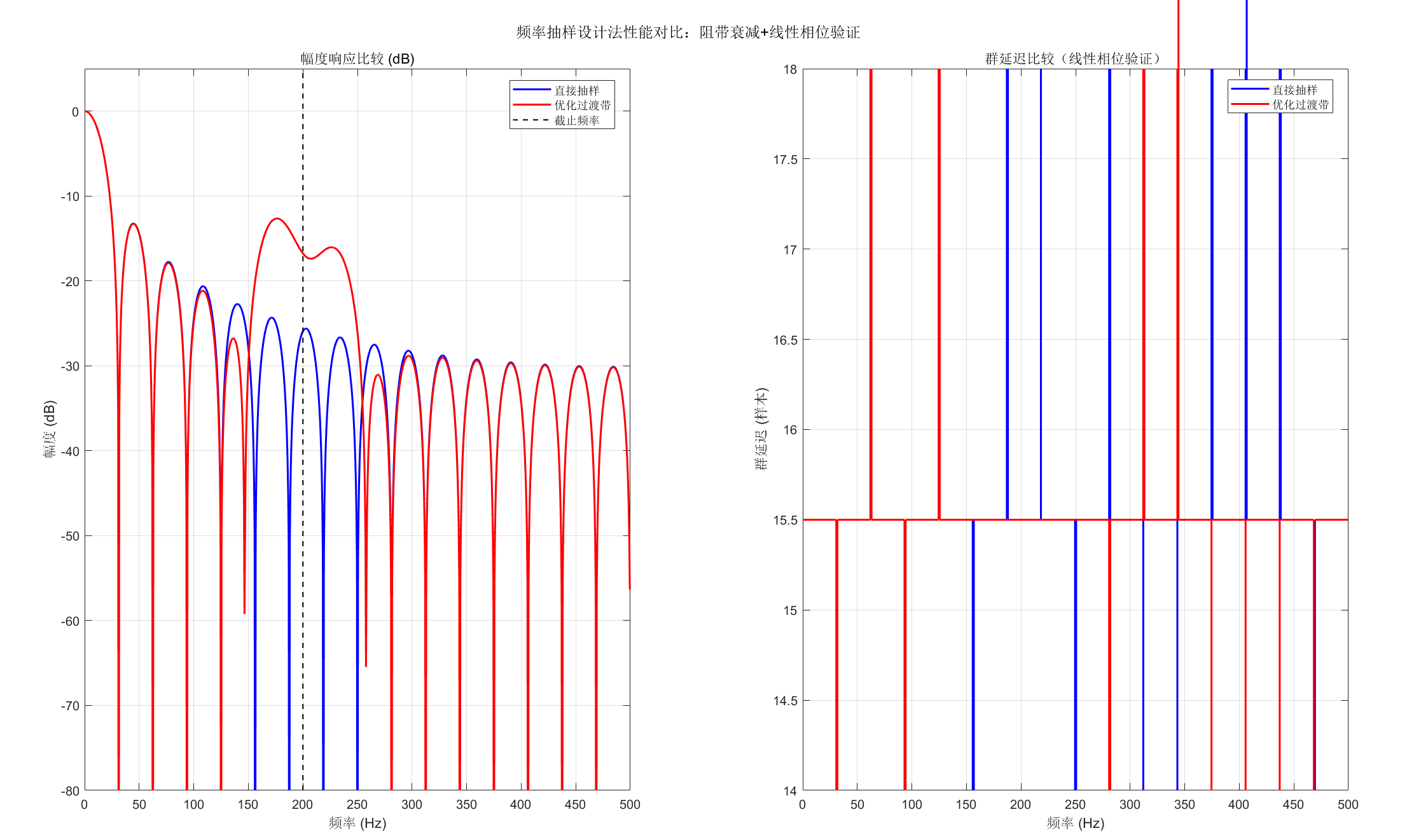

8.5 等波纹最优设计法（Parks-McClellan算法）

8.5.1-8.5.5 等波纹最优设计原理

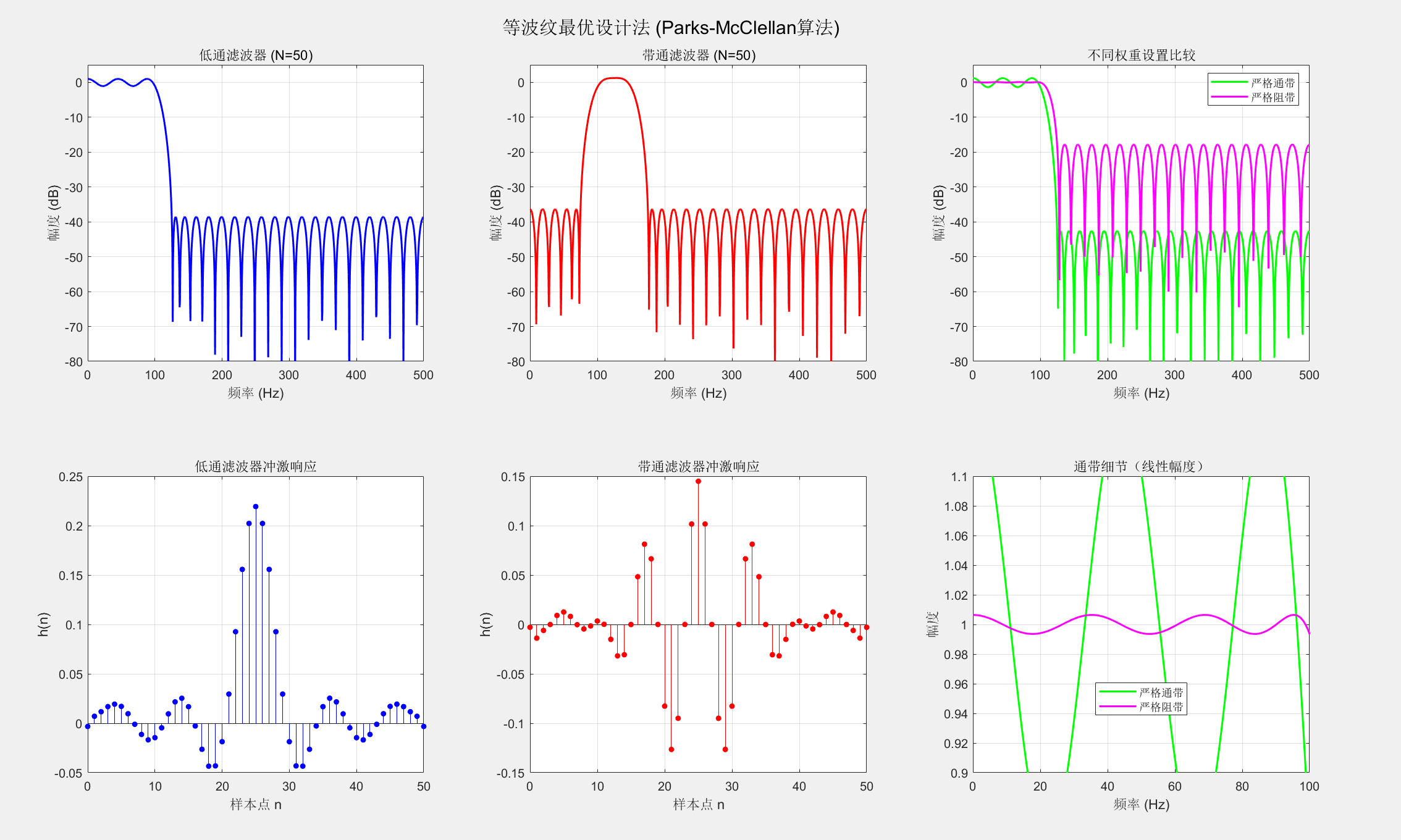
等波纹最优设计法通过切比雪夫逼近理论，在通带和阻带内实现等波纹波动，从而在给定阶数下获得最优的幅频特性。

Matlab 复制代码 
%% ============================================
% 8.5 等波纹最优设计法演示
% Parks-McClellan算法（Remez交换算法）
% ============================================

clear; close all; clc;

% 设计参数
Fs = 1000;          % 采样频率
N = 50;             % 滤波器阶数

% 设计1：低通滤波器
f_low = [0, 0.2, 0.25, 1];  % 频带边界（归一化频率）
a_low = [1, 1, 0, 0];       % 期望幅度
w_low = [1, 10];            % 权重：通带权重1，阻带权重10

% 使用remez算法设计
b_low = remez(N, f_low, a_low, w_low);

% 设计2：带通滤波器
f_band = [0, 0.15, 0.2, 0.3, 0.35, 1];
a_band = [0, 0, 1, 1, 0, 0];
w_band = [10, 1, 10];  % 阻带、通带、阻带权重

b_band = remez(N, f_band, a_band, w_band);

% 设计3：不同波纹约束的比较
% 设计3a：严格的通带波纹约束
w_strict = [0.5, 10];  % 通带权重小，阻带权重大
b_strict = remez(N, f_low, a_low, w_strict);

% 设计3b：严格的阻带衰减约束
w_relaxed = [10, 0.5];  % 通带权重大，阻带权重小
b_relaxed = remez(N, f_low, a_low, w_relaxed);

% 绘制设计结果
figure('Position', [100, 100, 1400, 900]);

% 低通滤波器的幅度响应
[H_low, w_low] = freqz(b_low, 1, 1024, Fs);
subplot(2,3,1);
plot(w_low, 20*log10(abs(H_low)), 'b', 'LineWidth', 1.5);
title(sprintf('低通滤波器 (N=%d)', N));
xlabel('频率 (Hz)'); ylabel('幅度 (dB)'); grid on;
xlim([0, Fs/2]); ylim([-80, 5]);

% 低通滤波器的冲激响应
subplot(2,3,4);
stem(0:N, b_low, 'b', 'filled', 'MarkerSize', 4);
title('低通滤波器冲激响应');
xlabel('样本点 n'); ylabel('h(n)'); grid on;

% 带通滤波器的幅度响应
[H_band, w_band] = freqz(b_band, 1, 1024, Fs);
subplot(2,3,2);
plot(w_band, 20*log10(abs(H_band)), 'r', 'LineWidth', 1.5);
title(sprintf('带通滤波器 (N=%d)', N));
xlabel('频率 (Hz)'); ylabel('幅度 (dB)'); grid on;
xlim([0, Fs/2]); ylim([-80, 5]);

% 带通滤波器的冲激响应
subplot(2,3,5);
stem(0:N, b_band, 'r', 'filled', 'MarkerSize', 4);
title('带通滤波器冲激响应');
xlabel('样本点 n'); ylabel('h(n)'); grid on;

% 不同权重设置的比较
[H_strict, w_s] = freqz(b_strict, 1, 1024, Fs);
[H_relaxed, w_r] = freqz(b_relaxed, 1, 1024, Fs);
subplot(2,3,3);
plot(w_s, 20*log10(abs(H_strict)), 'g', 'LineWidth', 1.5); hold on;
plot(w_r, 20*log10(abs(H_relaxed)), 'm', 'LineWidth', 1.5);
title('不同权重设置比较');
xlabel('频率 (Hz)'); ylabel('幅度 (dB)'); grid on;
legend('严格通带', '严格阻带', 'Location', 'best');
xlim([0, Fs/2]); ylim([-80, 5]);

% 绘制通带细节（线性幅度）
subplot(2,3,6);
plot(w_s, abs(H_strict), 'g', 'LineWidth', 1.5); hold on;
plot(w_r, abs(H_relaxed), 'm', 'LineWidth', 1.5);
title('通带细节（线性幅度）');
xlabel('频率 (Hz)'); ylabel('幅度'); grid on;
legend('严格通带', '严格阻带', 'Location', 'best');
xlim([0, 100]); ylim([0.9, 1.1]);

sgtitle('等波纹最优设计法 (Parks-McClellan算法)');

%% 比较不同设计方法的性能
% 设计相同规格的滤波器，比较窗函数法和等波纹法
f_pass = 150;      % 通带截止频率
f_stop = 200;      % 阻带起始频率
delta_p = 0.01;    % 通带波纹
delta_s = 0.001;   % 阻带波纹（-60dB）

% 使用firpmord估算所需阶数
[N_est, f0, a0, w0] = firpmord([f_pass, f_stop], [1, 0], [delta_p, delta_s], Fs);

% 设计等波纹滤波器
b_equiripple = firpm(N_est, f0, a0, w0);

% 设计窗函数法滤波器（使用凯塞窗，根据规格计算beta）
A = -20*log10(delta_s);  % 阻带衰减(dB)
if A > 50
    beta = 0.1102*(A-8.7);
elseif A >= 21
    beta = 0.5842*(A-21)^0.4 + 0.07886*(A-21);
else
    beta = 0;
end

% 计算所需窗长度
M = ceil((A-8)/(2.285*2*pi*(f_stop-f_pass)/Fs));
if mod(M,2) == 0
    M = M + 1;  % 确保奇数长度
end

% 设计凯塞窗滤波器
b_kaiser = fir1(M-1, (f_pass+f_stop)/Fs, 'low', kaiser(M, beta));

% 比较两种方法的性能
figure('Position', [100, 100, 1400, 600]);

% 幅度响应比较
[H_eq, w_eq] = freqz(b_equiripple, 1, 1024, Fs);
[H_k, w_k] = freqz(b_kaiser, 1, 1024, Fs);

subplot(1,2,1);
plot(w_eq, 20*log10(abs(H_eq)), 'b', 'LineWidth', 1.5); hold on;
plot(w_k, 20*log10(abs(H_k)), 'r--', 'LineWidth', 1.5);
plot([0, f_pass], [-20*log10(1-delta_p), -20*log10(1-delta_p)], 'k:', 'LineWidth', 1);
plot([0, f_pass], [-20*log10(1+delta_p), -20*log10(1+delta_p)], 'k:', 'LineWidth', 1);
plot([f_stop, Fs/2], [-20*log10(delta_s), -20*log10(delta_s)], 'k:', 'LineWidth', 1);
plot([f_pass, f_pass], [-100, 5], 'k--', 'LineWidth', 1);
plot([f_stop, f_stop], [-100, 5], 'k--', 'LineWidth', 1);
title('幅度响应比较 (dB)');
xlabel('频率 (Hz)'); ylabel('幅度 (dB)'); grid on;
legend('等波纹法', '凯塞窗法', '设计规格', 'Location', 'best');
xlim([0, Fs/2]); ylim([-100, 5]);

% 通带细节比较（线性幅度）
subplot(1,2,2);
plot(w_eq, abs(H_eq), 'b', 'LineWidth', 1.5); hold on;
plot(w_k, abs(H_k), 'r--', 'LineWidth', 1.5);
plot([0, f_pass], [1-delta_p, 1-delta_p], 'k:', 'LineWidth', 1);
plot([0, f_pass], [1+delta_p, 1+delta_p], 'k:', 'LineWidth', 1);
title('通带细节比较（线性幅度）');
xlabel('频率 (Hz)'); ylabel('幅度'); grid on;
legend('等波纹法', '凯塞窗法', '设计规格', 'Location', 'best');
xlim([0, f_pass*1.5]); ylim([1-delta_p*2, 1+delta_p*2]);

sgtitle('等波纹最优设计与窗函数法性能比较');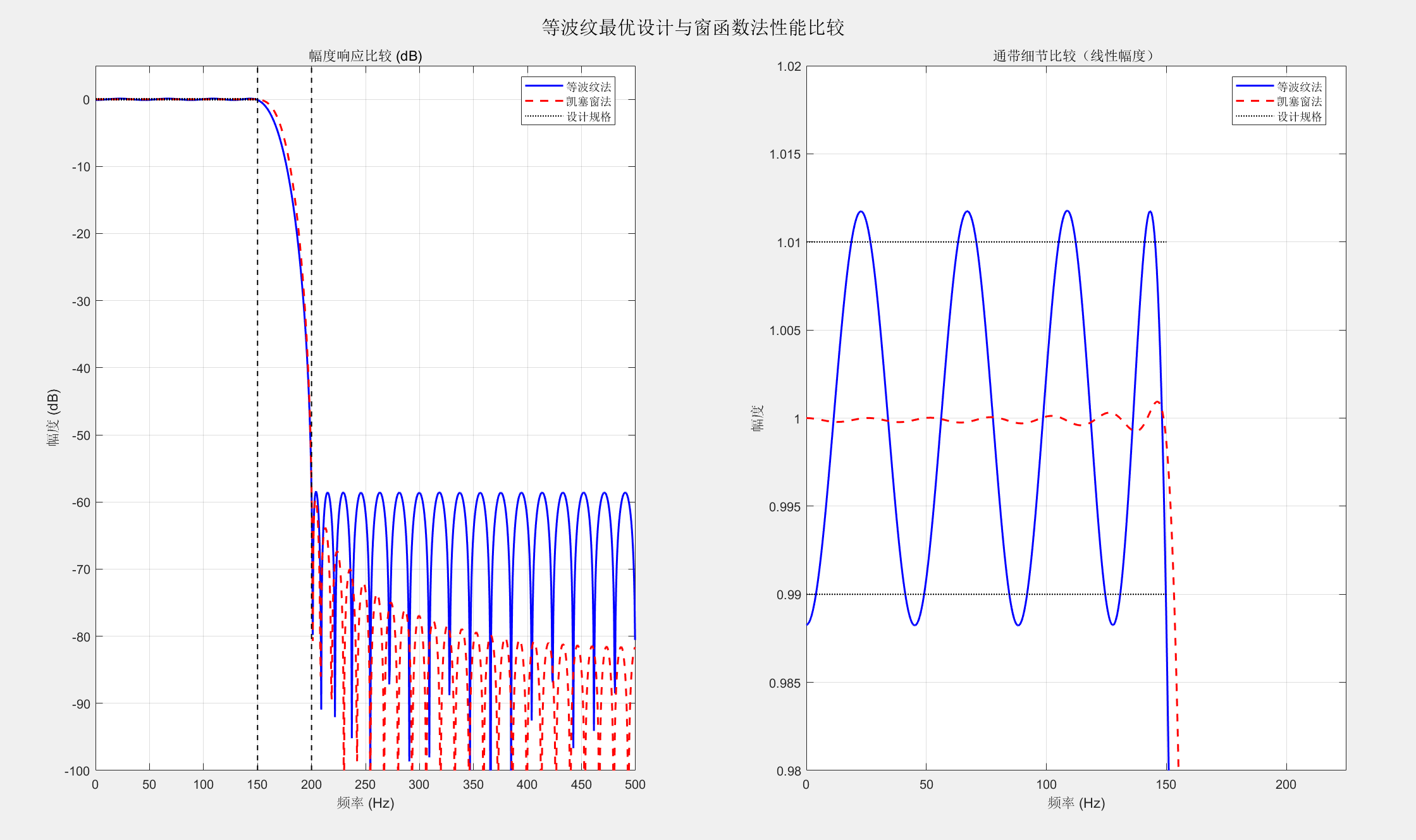

8.6 MATLAB函数及例题

8.6.1-8.6.4 MATLAB函数综合应用

Matlab 复制代码 
%% ============================================
% 8.6 MATLAB函数综合应用示例
% ============================================

clear; close all; clc;

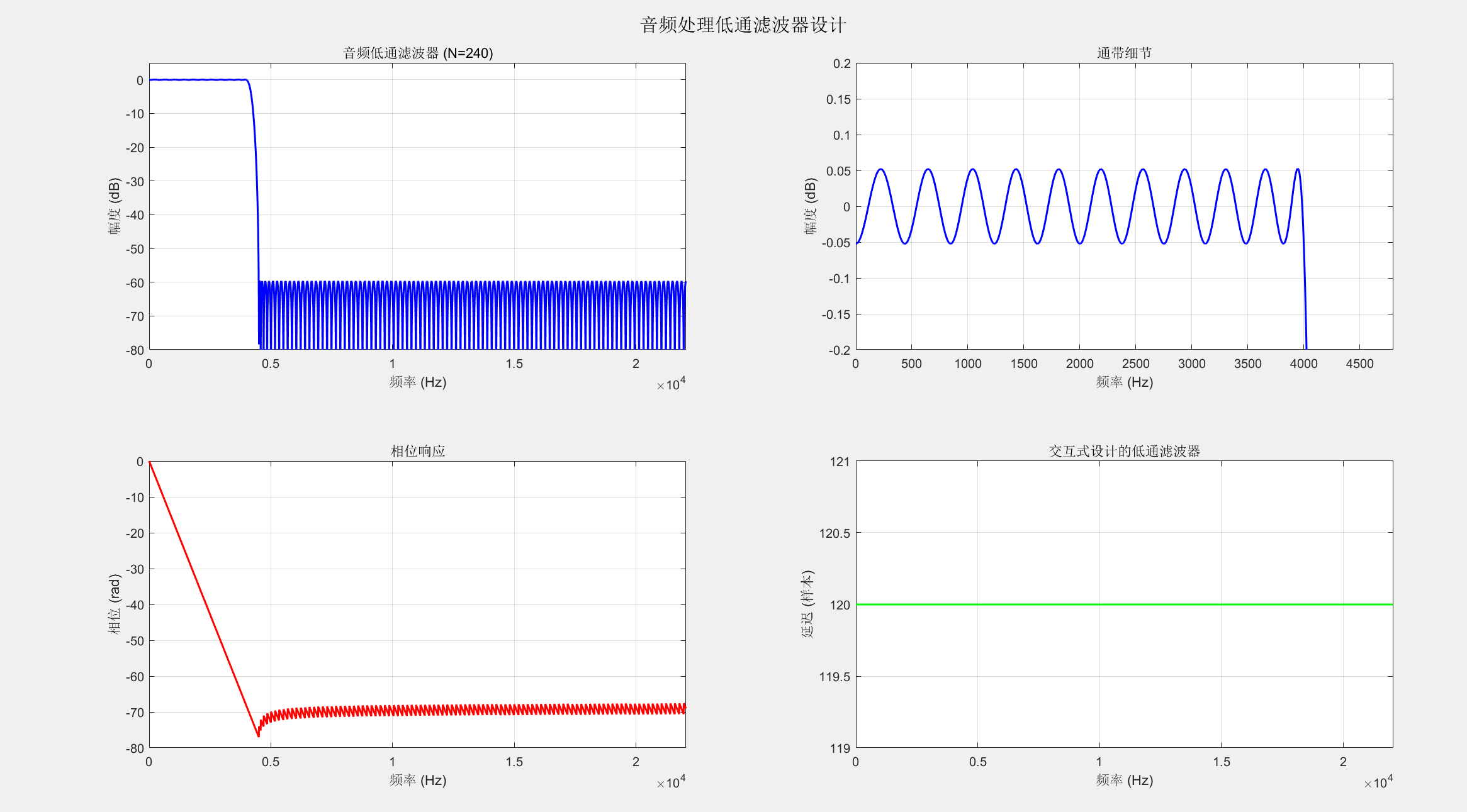
%% 示例1：设计一个音频处理用的低通滤波器
% 要求：采样率44.1kHz，通带0-4kHz，阻带起始4.5kHz，通带波纹0.1dB，阻带衰减60dB

Fs_audio = 44100;          % 音频采样率
fpass = 4000;              % 通带截止频率
fstop = 4500;              % 阻带起始频率
apass = 0.1;               % 通带波纹(dB)
astop = 60;                % 阻带衰减(dB)

% 将dB值转换为线性值
delta_p = (10^(apass/20)-1)/(10^(apass/20)+1);
delta_s = 10^(-astop/20);

% 使用firpmord估算阶数
[N_audio, fo, ao, wo] = firpmord([fpass, fstop], [1, 0], [delta_p, delta_s], Fs_audio);

% 设计等波纹滤波器
b_audio = firpm(N_audio, fo, ao, wo);

% 分析滤波器性能
[H_audio, f_audio] = freqz(b_audio, 1, 4096, Fs_audio);

figure('Position', [100, 100, 1200, 800]);

% 幅度响应
subplot(2,2,1);
plot(f_audio, 20*log10(abs(H_audio)), 'b', 'LineWidth', 1.5);
title(sprintf('音频低通滤波器 (N=%d)', N_audio));
xlabel('频率 (Hz)'); ylabel('幅度 (dB)'); grid on;
xlim([0, Fs_audio/2]); ylim([-80, 5]);

% 通带细节
subplot(2,2,2);
plot(f_audio, 20*log10(abs(H_audio)), 'b', 'LineWidth', 1.5);
title('通带细节');
xlabel('频率 (Hz)'); ylabel('幅度 (dB)'); grid on;
xlim([0, fpass*1.2]); ylim([-apass*2, apass*2]);

% 相位响应
subplot(2,2,3);
plot(f_audio, unwrap(angle(H_audio)), 'r', 'LineWidth', 1.5);
title('相位响应');
xlabel('频率 (Hz)'); ylabel('相位 (rad)'); grid on;
xlim([0, Fs_audio/2]);

% 群延迟
[gd_audio, f_gd] = grpdelay(b_audio, 1, 1024, Fs_audio);
subplot(2,2,4);
plot(f_gd, gd_audio, 'g', 'LineWidth', 1.5);
title('群延迟');
xlabel('频率 (Hz)'); ylabel('延迟 (样本)'); grid on;
xlim([0, Fs_audio/2]);

sgtitle('音频处理低通滤波器设计');

%% 示例2：设计一个希尔伯特变换器（90度移相器）
% 希尔伯特变换器用于生成解析信号

N_hilbert = 51;  % 奇数阶数，类型III线性相位

% 使用firpm设计希尔伯特变换器
f_hilbert = [0.05, 0.95];  % 工作频带，避开直流和Nyquist频率
a_hilbert = [1, 1];        % 幅度为1
b_hilbert = firpm(N_hilbert-1, f_hilbert, a_hilbert, 'hilbert');

% 分析希尔伯特变换器
[H_hilbert, w_hilbert] = freqz(b_hilbert, 1, 1024);

figure('Position', [100, 100, 1200, 600]);

% 幅度响应
subplot(1,2,1);
plot(w_hilbert/pi, abs(H_hilbert), 'b', 'LineWidth', 1.5);
title(sprintf('希尔伯特变换器幅度响应 (N=%d)', N_hilbert));
xlabel('归一化频率 (\times\pi rad/sample)');
ylabel('幅度'); grid on;
xlim([0, 1]); ylim([0, 1.2]);

% 相位响应
subplot(1,2,2);
plot(w_hilbert/pi, angle(H_hilbert), 'r', 'LineWidth', 1.5);
title('希尔伯特变换器相位响应');
xlabel('归一化频率 (\times\pi rad/sample)');
ylabel('相位 (rad)'); grid on;
xlim([0, 1]); ylim([-pi, pi]);

sgtitle('希尔伯特变换器设计');

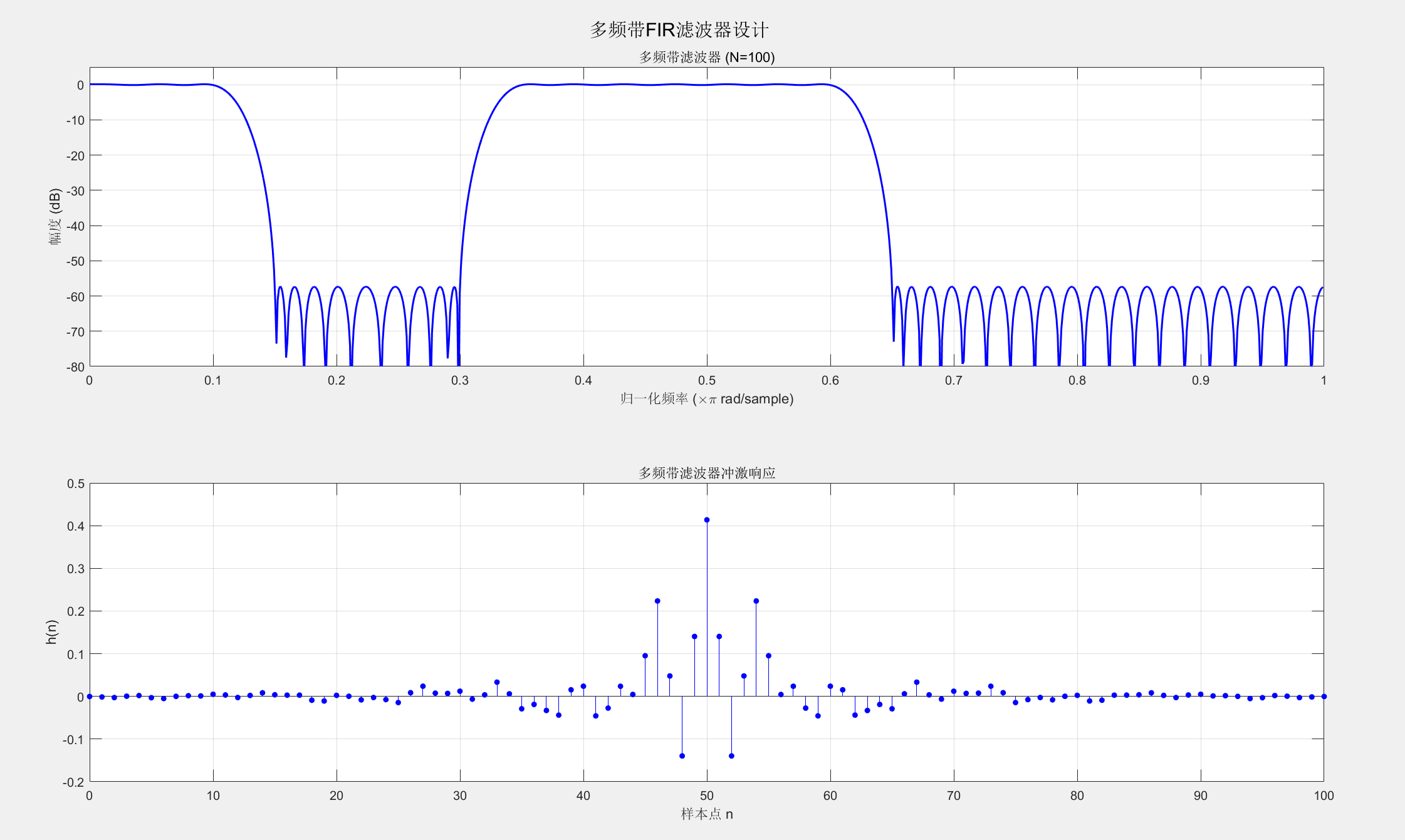
%% 示例3：多频带滤波器设计
% 设计一个三频带滤波器：低通、带通、高通组合

N_multiband = 100;
f_bands = [0, 0.1, 0.15, 0.3, 0.35, 0.6, 0.65, 1];
a_bands = [1, 1, 0, 0, 1, 1, 0, 0];  % 低通+带通
w_bands = [1, 10, 1, 10];  % 权重

b_multiband = firpm(N_multiband, f_bands, a_bands, w_bands);

% 分析多频带滤波器
[H_multi, w_multi] = freqz(b_multiband, 1, 1024);

figure('Position', [100, 100, 1000, 800]);

% 幅度响应
subplot(2,1,1);
plot(w_multi/pi, 20*log10(abs(H_multi)), 'b', 'LineWidth', 1.5);
title(sprintf('多频带滤波器 (N=%d)', N_multiband));
xlabel('归一化频率 (\times\pi rad/sample)');
ylabel('幅度 (dB)'); grid on;
xlim([0, 1]); ylim([-80, 5]);

% 冲激响应
subplot(2,1,2);
stem(0:N_multiband, b_multiband, 'b', 'filled', 'MarkerSize', 4);
title('多频带滤波器冲激响应');
xlabel('样本点 n'); ylabel('h(n)'); grid on;

sgtitle('多频带FIR滤波器设计');

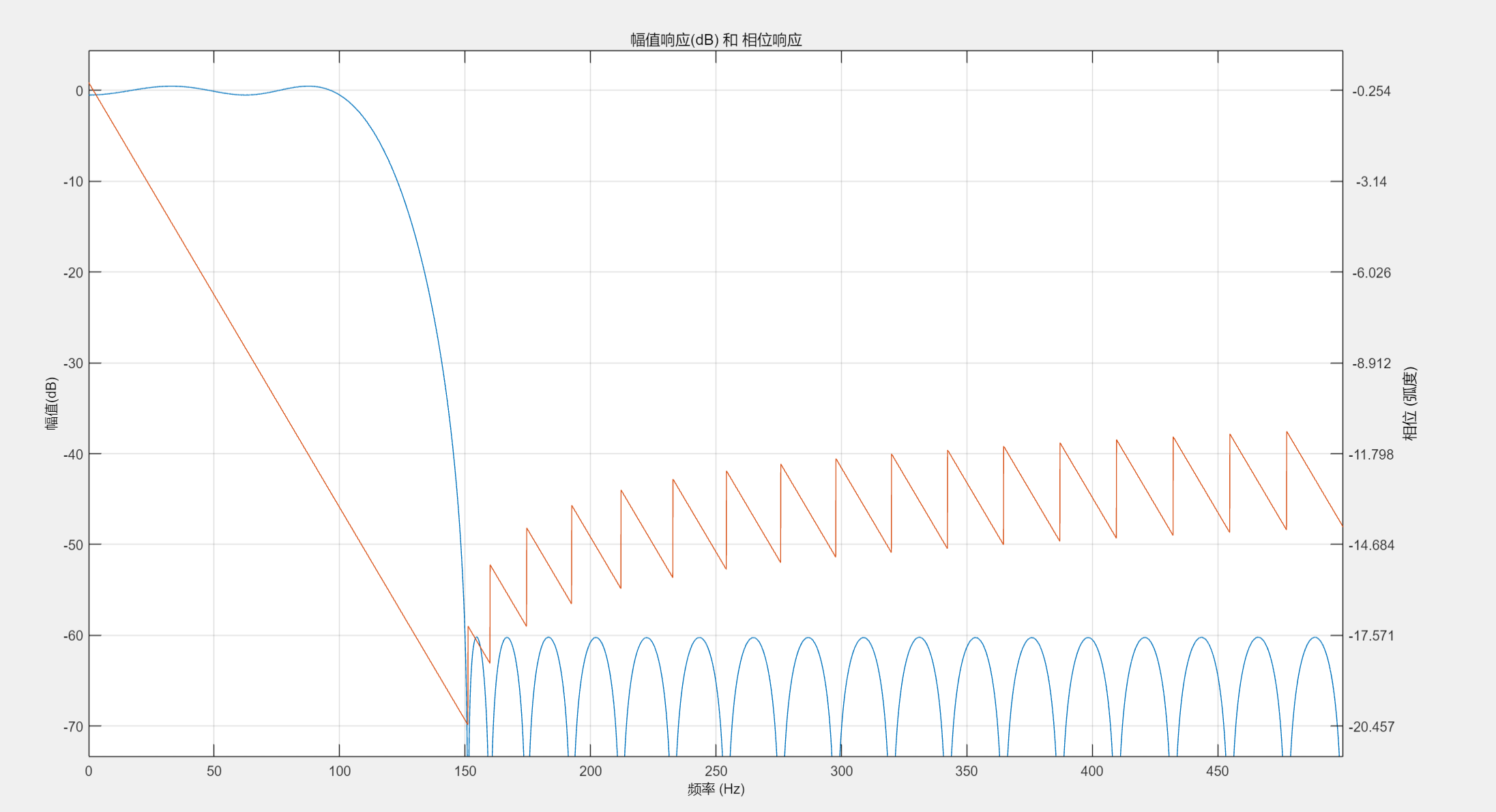
%% 示例4：滤波器设计GUI演示（交互式设计）
% 注意：此部分代码需要用户交互，运行时会打开滤波器设计工具

disp('正在打开滤波器设计工具...');
disp('在打开的窗口中，您可以交互式地设计滤波器。');

% 打开滤波器设计工具（FDATool的简化版本）
fdesign = 'lowpassfir';  % 低通FIR滤波器
Fs = 1000;               % 采样频率
Fpass = 100;             % 通带频率
Fstop = 150;             % 阻带频率
Apass = 1;               % 通带波纹(dB)
Astop = 60;              % 阻带衰减(dB)

% 使用designfilt函数设计滤波器
d = designfilt(fdesign, 'SampleRate', Fs, ...
    'PassbandFrequency', Fpass, 'StopbandFrequency', Fstop, ...
    'PassbandRipple', Apass, 'StopbandAttenuation', Astop);

% 显示滤波器信息
fvtool(d, 'Analysis', 'freq');
title('交互式设计的低通滤波器');

% 获取滤波器系数
b_design = d.Coefficients;

% 显示滤波器规格
disp(' ');
disp('===== 滤波器规格 =====');
disp(['采样频率: ', num2str(Fs), ' Hz']);
disp(['通带频率: ', num2str(Fpass), ' Hz']);
disp(['阻带频率: ', num2str(Fstop), ' Hz']);
disp(['通带波纹: ', num2str(Apass), ' dB']);
disp(['阻带衰减: ', num2str(Astop), ' dB']);
disp(['滤波器阶数: ', num2str(length(b_design)-1)]);
disp('=====================');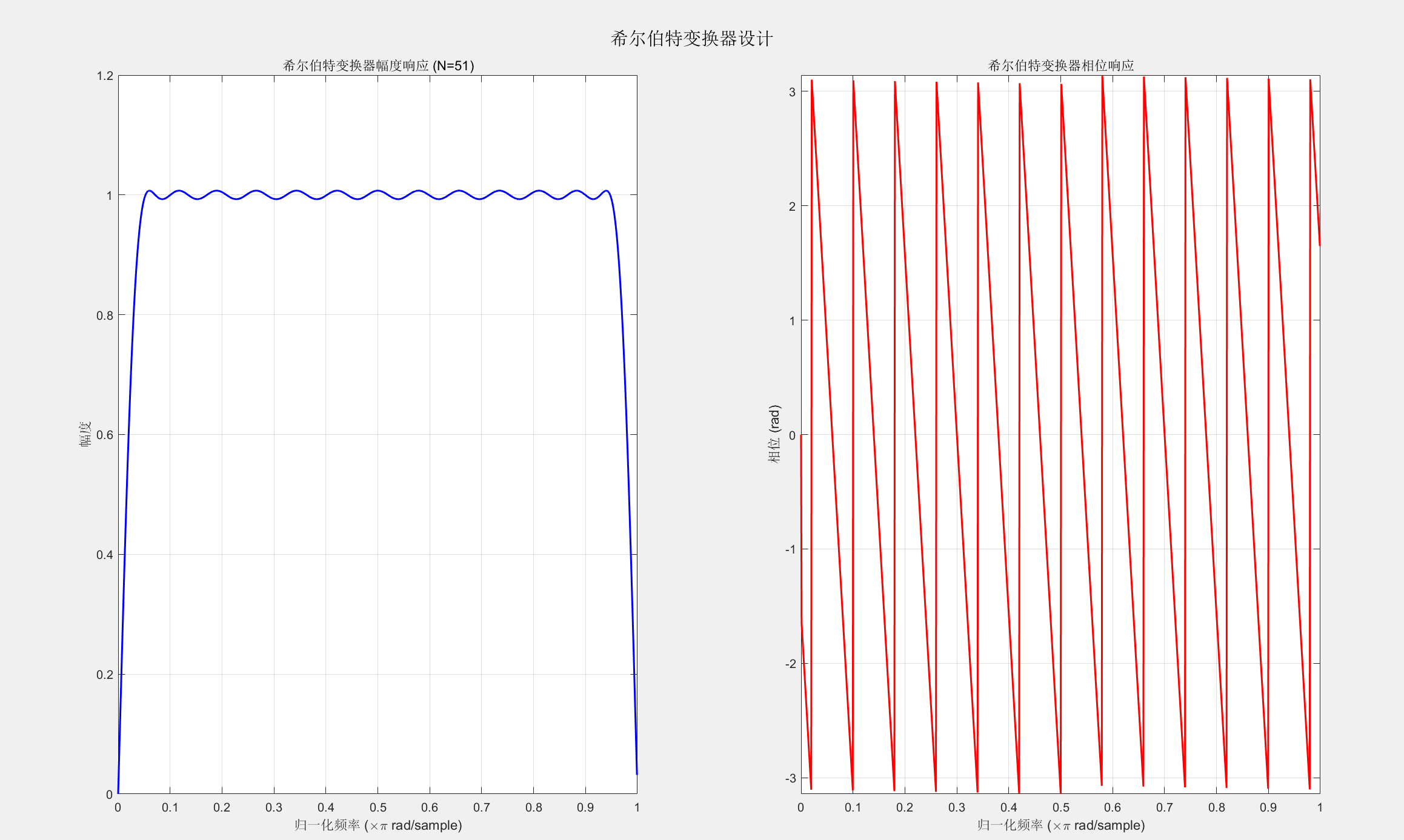

流程图：FIR滤波器设计方法选择

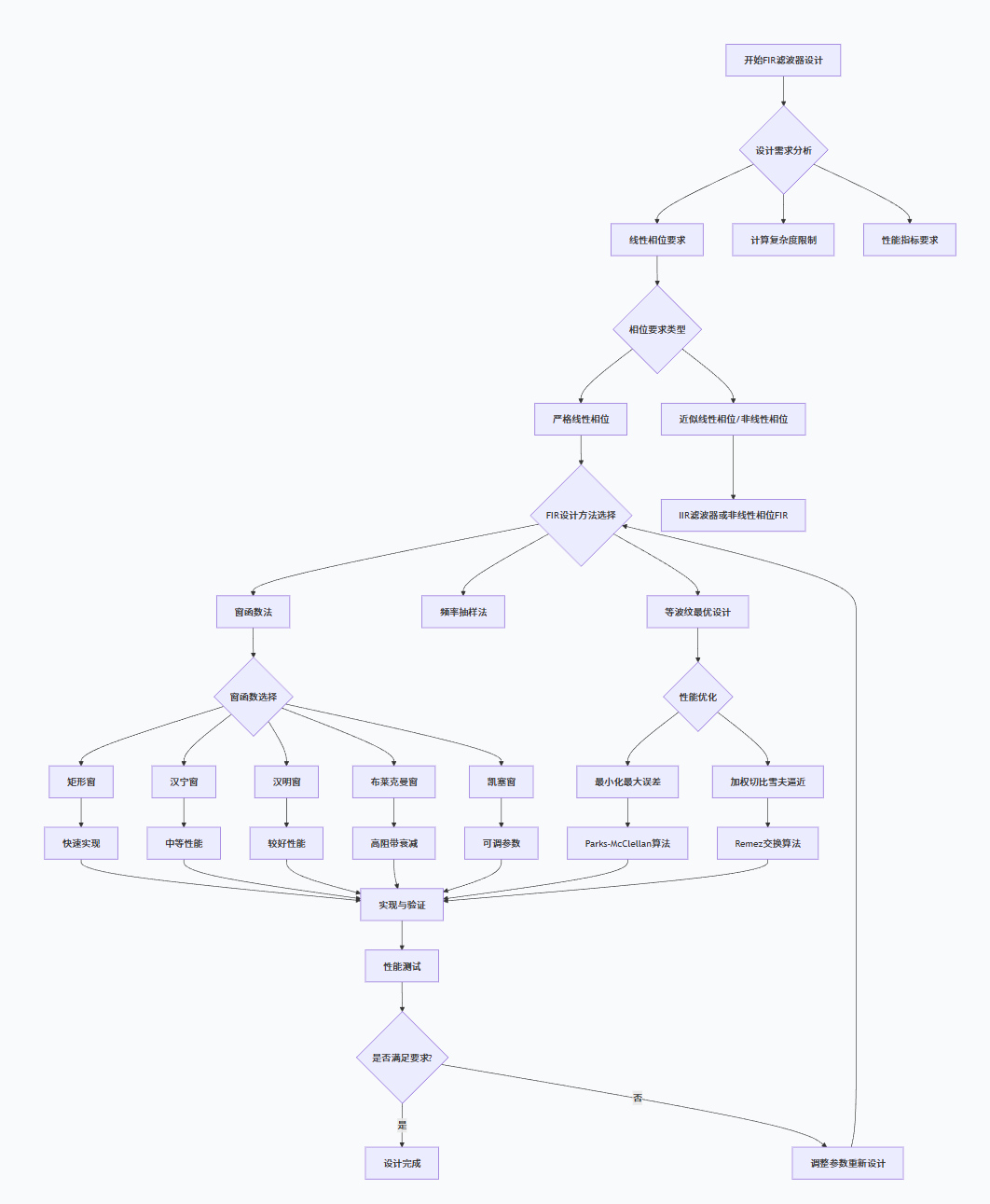
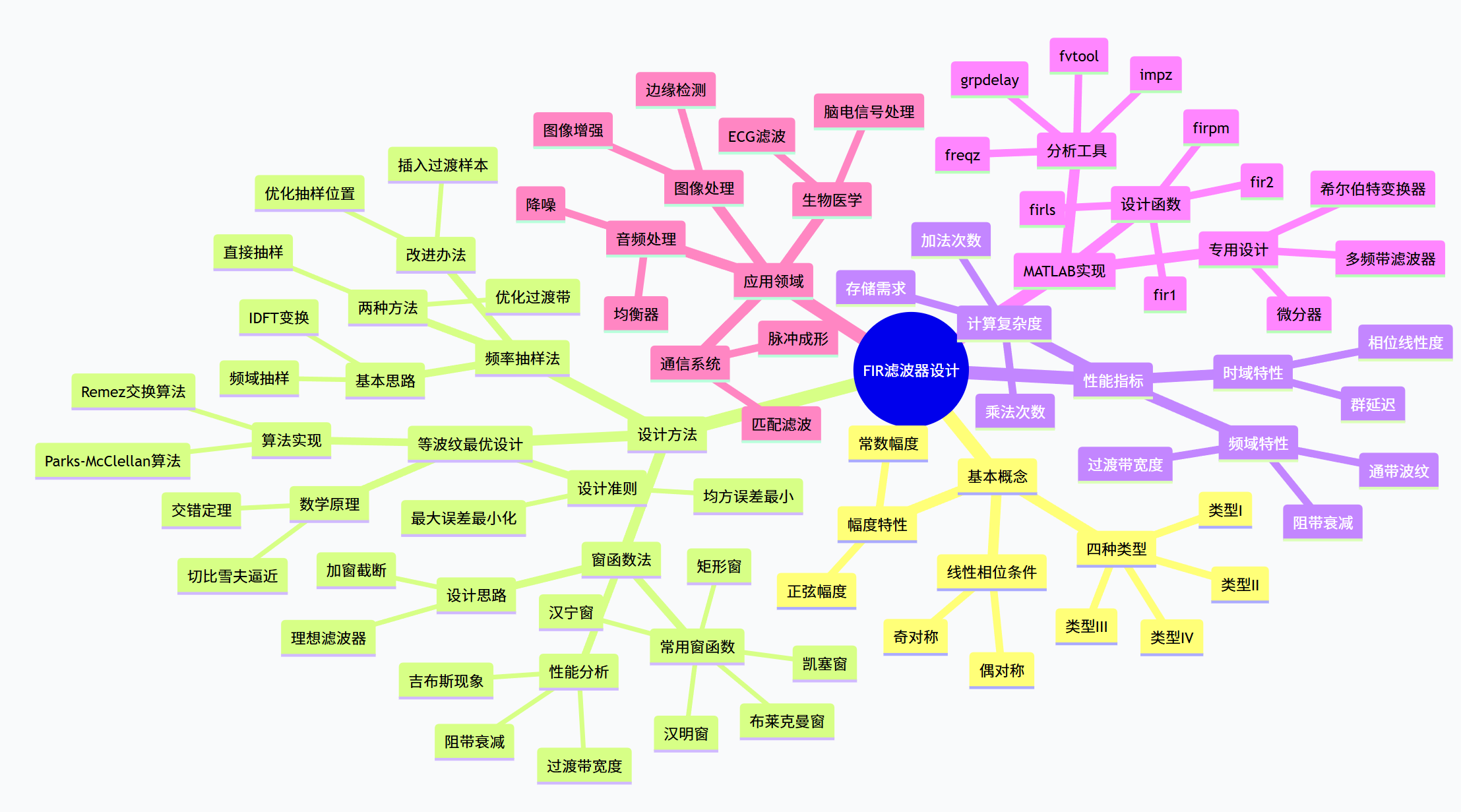
思维导图：FIR滤波器设计知识体系

总结

本章系统介绍了FIR滤波器的三种主要设计方法：

  1. 窗函数法：最简单直观，适合快速原型设计，但难以精确控制频率响应特性。

  2. 频率抽样法：直接在频域设计，适合频率响应形状复杂的情况，但过渡带性能较差。

  3. 等波纹最优设计法：基于切比雪夫逼近理论，在给定阶数下获得最优性能，是工程实践中最常用的方法。

每种方法都有其适用场景：

  • 对实时性要求高、计算资源有限的场合，可选用窗函数法。

  • 需要特殊频率响应形状时，可考虑频率抽样法。

  • 对性能有严格要求的场合，应使用等波纹最优设计法。

MATLAB提供了丰富的FIR滤波器设计工具，掌握这些工具的使用方法能够大大提高滤波器设计的效率和质量。

习题

  1. 设计一个截止频率为0.3π的FIR低通滤波器，分别用矩形窗、汉宁窗和汉明窗实现，比较它们的幅度响应和相位响应。

  2. 使用频率抽样法设计一个31点的FIR带通滤波器，通带为0.2π-0.4π。

  3. 用Parks-McClellan算法设计一个60阶的FIR低通滤波器，通带截止频率为0.25π，阻带起始频率为0.35π，通带波纹不大于0.1dB，阻带衰减不小于50dB。

  4. 设计一个希尔伯特变换器，实现90度相移，分析其幅度和相位特性。

  5. 比较窗函数法和等波纹法在设计相同规格滤波器时的性能差异。

相关推荐
AndrewHZ2 小时前
【图像处理与ISP技术】图像质量评价领域经典算法一览
图像处理·人工智能·深度学习·算法·机器学习·图像质量评价·iqa
guygg8811 小时前
NOMA功率分配与64 QAM调制中的SIC的MATLAB仿真
开发语言·matlab
TracyCoder12311 小时前
LeetCode Hot100（15/100）——54. 螺旋矩阵
算法·leetcode·矩阵
u01092727112 小时前
C++中的策略模式变体
开发语言·c++·算法
2501_9418372612 小时前
停车场车辆检测与识别系统-YOLOv26算法改进与应用分析
算法·yolo
六义义13 小时前
java基础十二
java·数据结构·算法
四维碎片13 小时前
QSettings + INI 笔记
笔记·qt·算法
Tansmjs13 小时前
C++与GPU计算（CUDA）
开发语言·c++·算法
独自破碎E14 小时前
【优先级队列】主持人调度（二）
算法
热门推荐
01GitHub 镜像站点02【网络安全测试】Burp Suite工具使用说明、配置及常见问题（有关必回）03OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)04Claude Code Skills 实用使用手册05UV安装并设置国内源06struts2 XML外部实体注入漏洞复现（CVE-2025-68493）07在Trae中使用Pencil MCP08Open Code教程（四）| 高级配置与集成09在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）10Linux下V2Ray安装配置指南