文章目录
-
- 引言:从"平均"到"智能"的图像处理进化
- 一、非线性滤波的哲学:从均匀处理到智能区分
-
- [1.1 线性滤波的局限性](#1.1 线性滤波的局限性)
- [1.2 非线性滤波的核心思想](#1.2 非线性滤波的核心思想)
- 二、中值滤波:统计排序的艺术
-
- [2.1 算法原理与实现](#2.1 算法原理与实现)
- [2.2 数学原理可视化](#2.2 数学原理可视化)
- [2.3 应用场景与局限性](#2.3 应用场景与局限性)
- 三、双边滤波:空间与值域的双重智慧
-
- [3.1 算法设计哲学](#3.1 算法设计哲学)
- [3.2 完整计算过程详解](#3.2 完整计算过程详解)
- [3.3 计算流程可视化](#3.3 计算流程可视化)
- [3.4 参数影响分析](#3.4 参数影响分析)
- [3.5 美颜应用原理](#3.5 美颜应用原理)
- 四、技术对比与选择指南
-
- [4.1 滤波技术全景对比](#4.1 滤波技术全景对比)
- [4.2 实战选择指南](#4.2 实战选择指南)
- [4.3 参数调优实战](#4.3 参数调优实战)
- 五、总结与启示
- 附录:实用代码片段
引言:从"平均"到"智能"的图像处理进化
数字图像处理领域的发展如同一次视觉认知的革命。在早期,线性滤波技术如均值滤波和高斯滤波如同"无差别平均器",它们在减少噪声的同时也模糊了图像的重要特征。而现代非线性滤波技术则更像"智能编辑",能够区分图像中的噪声、纹理和边缘,实现有针对性的处理。本文将通过第一性原理,深入剖析非线性滤波的核心思想,特别是中值滤波和双边滤波的工作原理、应用场景及实现细节。
一、非线性滤波的哲学:从均匀处理到智能区分
1.1 线性滤波的局限性
传统的线性滤波技术基于一个基本假设:图像信号和噪声在频域上可分离。这种假设在处理简单噪声时有效,但在面对实际复杂场景时暴露了本质缺陷:
均值滤波示例(3×3窗口):
原始像素值: [10, 20, 30, 40, 100, 60, 70, 80, 90]
平均值 = (10+20+30+40+100+60+70+80+90)/9 = 55.6问题显而易见:当存在极值点(可能是噪声,也可能是重要边缘)时,简单的平均计算无法智能区分,导致边缘模糊 和细节丢失。
1.2 非线性滤波的核心思想
非线性滤波的核心突破在于放弃了"线性加权平均"的传统思路,转而采用基于逻辑判断的自适应处理。这种处理方式能够根据局部图像特性动态调整滤波策略:
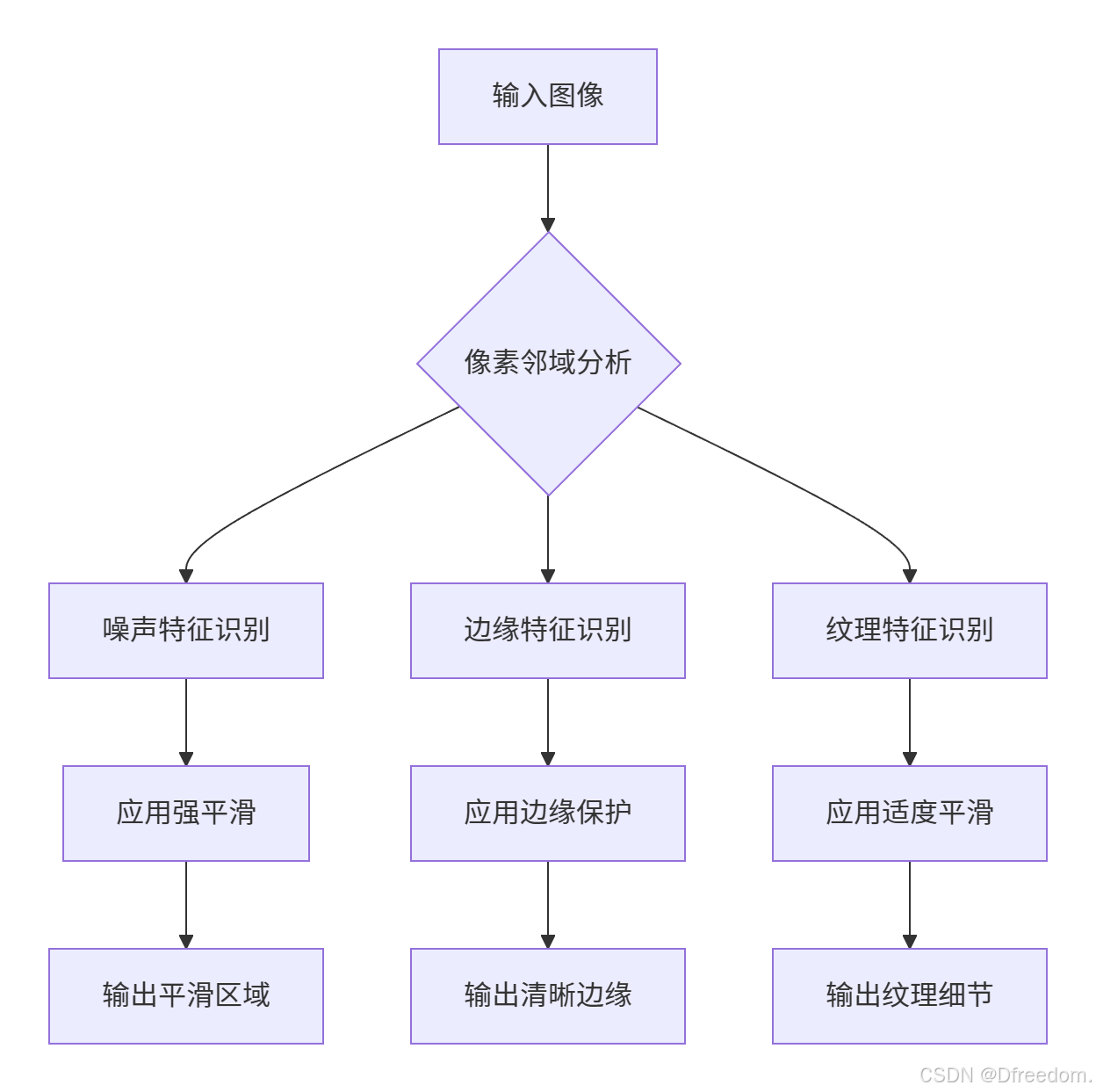
二、中值滤波:统计排序的艺术
2.1 算法原理与实现
中值滤波算法的核心可以用一句话概括:用邻域像素灰度值的中位数替代当前像素值。这种基于排序的方法使其对极值点(异常点)具有天然抵抗力。
# 中值滤波的Python实现示例
def median_filter(image, kernel_size=3):
"""应用中值滤波"""
pad_size = kernel_size // 2
padded = np.pad(image, pad_size, mode='edge')
result = np.zeros_like(image)
for i in range(image.shape[0]):
for j in range(image.shape[1]):
# 提取邻域
neighborhood = padded[i:i+kernel_size, j:j+kernel_size]
# 排序并取中值
result[i, j] = np.median(neighborhood)
return result2.2 数学原理可视化
中值滤波的效果可以通过以下数学特性理解:
邻域像素值: [15, 18, 20, 22, 255, 24, 26, 28, 30]
排序后: [15, 18, 20, 22, 24, 26, 28, 30, 255]
中值 = 24
原始中心值 = 255(很可能是椒盐噪声)这个简单的例子展示了中值滤波如何有效去除极端噪声点(255),而不会像均值滤波那样将所有像素"拉平"。
2.3 应用场景与局限性
中值滤波的优势领域:
- 椒盐噪声去除:在文档扫描、医学影像中特别有效
- 边缘保持:相比线性滤波,能更好地保护锐利边缘
- 计算相对高效:对于小窗口,时间复杂度可接受
局限性分析:
- 对高斯噪声效果有限
- 可能破坏细线和角点特征
- 大窗口时计算成本显著增加
三、双边滤波:空间与值域的双重智慧
3.1 算法设计哲学
双边滤波的设计体现了双重适应性 的智慧:它同时考虑像素的空间邻近性 和值域相似性。这种双重考量使其能够实现"选择性平滑"------在均匀区域平滑,在边缘处保护。
3.2 完整计算过程详解
让我们通过一个具体的数值示例,完整演示双边滤波的计算过程:
示例设置
-
图像块(3×3,中心像素待滤波):
120 125 130 125 200 135 130 135 140注:中心像素值 200 明显高于周围,可能是一个亮点或小边缘
-
参数设置:
- 空间标准差 σ_s = 1.5
- 值域标准差 σ_r = 30
- 滤波窗口:3×3
第一步:计算空间权重
空间权重衡量几何距离的影响,遵循高斯分布:
空间权重公式:G_s = exp(-(dx²+dy²)/(2σ_s²))中心像素坐标为(0,0),各位置的空间权重计算如下表所示:
| 相对坐标 | 距离平方(d²) | 空间权重 G_s |
|---|---|---|
| (-1,-1) | 2 | exp(-2/4.5) ≈ 0.641 |
| (-1,0) | 1 | exp(-1/4.5) ≈ 0.801 |
| (-1,1) | 2 | exp(-2/4.5) ≈ 0.641 |
| (0,-1) | 1 | exp(-1/4.5) ≈ 0.801 |
| (0,0) | 0 | exp(0) = 1.000 |
| (0,1) | 1 | exp(-1/4.5) ≈ 0.801 |
| (1,-1) | 2 | exp(-2/4.5) ≈ 0.641 |
| (1,0) | 1 | exp(-1/4.5) ≈ 0.801 |
| (1,1) | 2 | exp(-2/4.5) ≈ 0.641 |
第二步:计算值域权重
值域权重基于像素值差异,是边缘保护的关键:
值域权重公式:G_r = exp(-(I_p-I_center)²/(2σ_r²))中心像素值 I_center=200,各像素值域权重计算:
| 像素值 I | 差值(I-200) | 差值平方 | 值域权重 G_r |
|---|---|---|---|
| 120 | 80 | 6400 | exp(-6400/1800) ≈ 0.029 |
| 125 | 75 | 5625 | exp(-5625/1800) ≈ 0.044 |
| 130 | 70 | 4900 | exp(-4900/1800) ≈ 0.068 |
| 125 | 75 | 5625 | exp(-5625/1800) ≈ 0.044 |
| 200 | 0 | 0 | exp(0) = 1.000 |
| 135 | 65 | 4225 | exp(-4225/1800) ≈ 0.099 |
| 130 | 70 | 4900 | exp(-4900/1800) ≈ 0.068 |
| 135 | 65 | 4225 | exp(-4225/1800) ≈ 0.099 |
| 140 | 60 | 3600 | exp(-3600/1800) ≈ 0.135 |
第三步:计算复合权重
复合权重 = 空间权重 × 值域权重:
| 位置 | 空间权重 G_s | 值域权重 G_r | 复合权重 W |
|---|---|---|---|
| (-1,-1) | 0.641 | 0.029 | 0.0186 |
| (-1,0) | 0.801 | 0.044 | 0.0352 |
| (-1,1) | 0.641 | 0.068 | 0.0436 |
| (0,-1) | 0.801 | 0.044 | 0.0352 |
| (0,0) | 1.000 | 1.000 | 1.0000 |
| (0,1) | 0.801 | 0.099 | 0.0793 |
| (1,-1) | 0.641 | 0.068 | 0.0436 |
| (1,0) | 0.801 | 0.099 | 0.0793 |
| (1,1) | 0.641 | 0.135 | 0.0865 |
总权重和 = 0.0186+0.0352+0.0436+0.0352+1.0000+0.0793+0.0436+0.0793+0.0865 = 1.4213
第四步:计算加权平均
加权像素值和 = Σ(像素值 × 复合权重):
= 120×0.0186 + 125×0.0352 + 130×0.0436 + 125×0.0352 + 200×1.0000 + 135×0.0793 + 130×0.0436 + 135×0.0793 + 140×0.0865
= 2.232 + 4.400 + 5.668 + 4.400 + 200.000 + 10.706 + 5.668 + 10.706 + 12.110
= 255.890
滤波后中心像素值 = 255.890 / 1.4213 ≈ 180.0
结果分析
原始中心像素值为 200,滤波后变为 180。这个结果体现了双边滤波的智能:
- 由于中心像素与周围差异大,周围像素的权重被显著降低
- 但中心像素自身权重为 1,保留了大部分原始值
- 最终结果比简单平均(约 137)更接近原始值,保护了可能的边缘或亮点
3.3 计算流程可视化
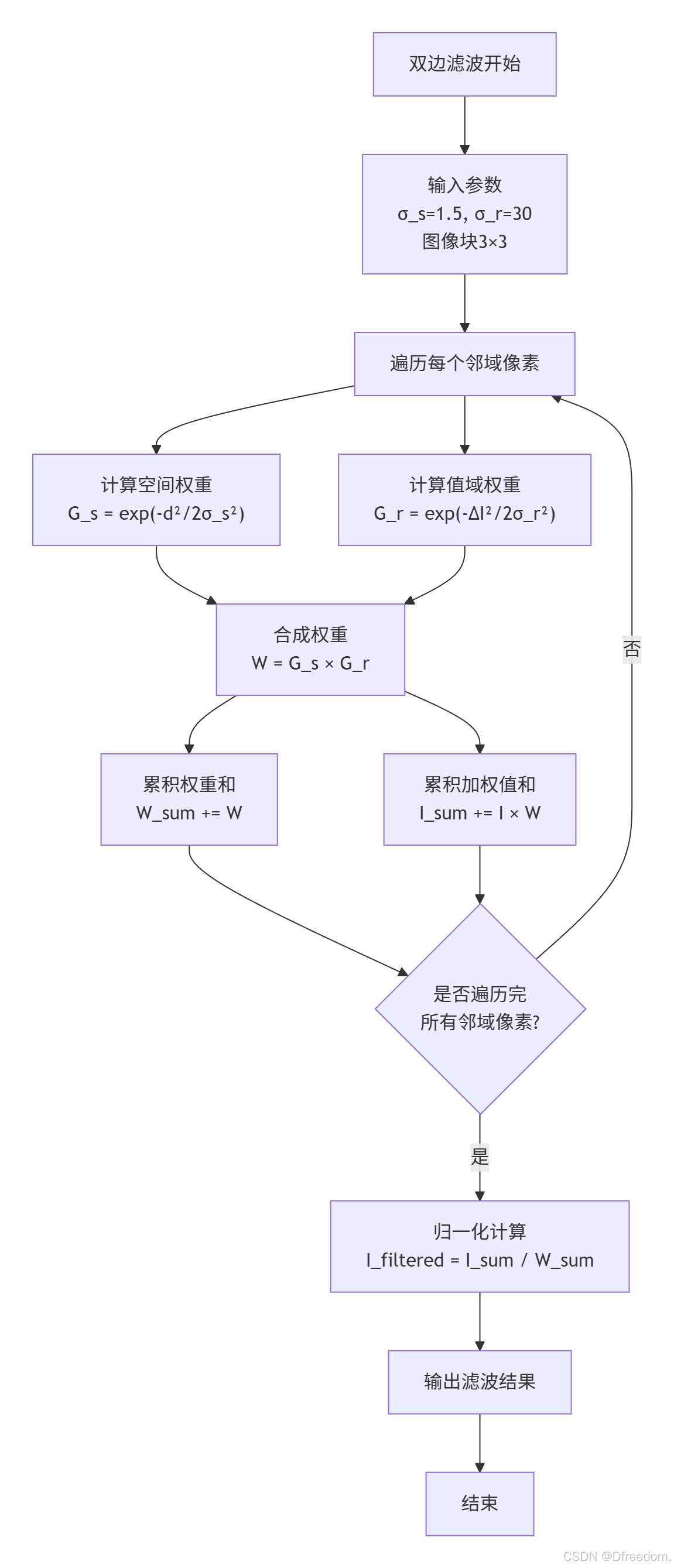
3.4 参数影响分析
双边滤波的效果高度依赖两个参数的选择:
空间标准差 σ_s 的影响:
- σ_s 较小时:只考虑紧邻像素,平滑效果局部化
- σ_s 较大时:考虑更大范围像素,平滑效果更广泛
- 经验公式:σ_s ≈ 0.5% × 图像对角线长度
值域标准差 σ_r 的影响:
- σ_r 较小时:只允许非常相似的像素参与平均,边缘保护强
- σ_r 较大时:允许差异较大的像素参与平均,平滑效果更强
- 经验公式:σ_r ≈ 0.1 × 图像灰度范围
3.5 美颜应用原理
在人像美颜中,双边滤波实现了"智能磨皮":
-
皮肤区域:像素值相近,值域权重大,平滑效果好
-
五官边缘:像素值突变,值域权重小,边缘保持清晰
-
过渡区域:根据相似度自适应调整平滑强度
美颜中的双边滤波应用示例
def beauty_filter(image, sigma_color=30, sigma_space=10):
"""美颜滤波函数"""
# 应用双边滤波
smoothed = cv2.bilateralFilter(
image,
d=9, # 滤波器直径
sigmaColor=sigma_color, # 值域标准差
sigmaSpace=sigma_space # 空间标准差
)# 可选:结合其他美颜技术 # 如锐化、对比度增强等 return smoothed
四、技术对比与选择指南
4.1 滤波技术全景对比
| 特性 | 均值滤波 | 高斯滤波 | 中值滤波 | 双边滤波 |
|---|---|---|---|---|
| 滤波类型 | 线性 | 线性 | 非线性 | 非线性 |
| 核心原理 | 算术平均 | 高斯加权平均 | 统计排序 | 双重权重 |
| 计算复杂度 | O(n) | O(n) | O(n log n) | O(n²) |
| 边缘保护 | 差 | 中等 | 好 | 优秀 |
| 椒盐噪声 | 效果有限 | 效果有限 | 优秀 | 好 |
| 高斯噪声 | 中等 | 好 | 效果有限 | 好 |
| 主要参数 | 窗口大小 | 窗口大小、σ | 窗口大小 | σ_s、σ_r |
| 典型应用 | 简单平滑 | 一般去噪 | 文档处理 | 美颜、边缘保持 |
4.2 实战选择指南
场景一:文档图像处理
问题:扫描文档中的椒盐噪声
推荐:中值滤波,窗口大小3×3
原因:有效去除黑白点噪声,保持文字边缘清晰场景二:人像美颜
问题:皮肤平滑同时保持五官清晰
推荐:双边滤波,σ_s=10-20, σ_r=20-40
原因:智能区分皮肤区域和边缘区域场景三:医学影像增强
问题:去除噪声同时保留组织边界
推荐:自适应双边滤波
原因:不同区域可能需要不同参数场景四:实时视频处理
问题:需要平衡效果和速度
推荐:分离双边滤波或导向滤波
原因:计算效率更高,适合实时应用4.3 参数调优实战
def optimize_bilateral_filter(image):
"""双边滤波参数优化示例"""
results = []
# 测试不同的参数组合
param_combinations = [
(5, 10), # 小空间范围,小值域范围
(10, 20), # 中等参数
(20, 40), # 大参数,更强平滑
(5, 40), # 小空间范围,大值域范围
(20, 10) # 大空间范围,小值域范围
]
for sigma_space, sigma_color in param_combinations:
filtered = cv2.bilateralFilter(
image, d=9,
sigmaColor=sigma_color,
sigmaSpace=sigma_space
)
# 评估滤波效果
edge_preservation = evaluate_edge_preservation(image, filtered)
noise_reduction = evaluate_noise_reduction(image, filtered)
results.append({
'params': (sigma_space, sigma_color),
'result': filtered,
'edge_score': edge_preservation,
'noise_score': noise_reduction
})
return results五、总结与启示
非线性滤波技术,特别是中值滤波和双边滤波,代表了图像处理从"盲目平均"到"智能感知"的重要转变。它们的核心智慧在于:
- 中值滤波:通过排序抵抗异常值,是处理椒盐噪声的首选
- 双边滤波:通过双重权重实现选择性平滑,是边缘保护的金标准
这些技术的成功启示我们,在处理复杂信号时:
- 简单模型可能无法捕捉复杂模式
- 自适应和上下文感知是关键
- 计算复杂度和效果需要平衡
附录:实用代码片段
import numpy as np
import cv2
import matplotlib.pyplot as plt
def visualize_filtering_effect(image_path):
"""可视化不同滤波效果"""
# 读取图像
img = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)
# 添加噪声
noisy = add_salt_pepper_noise(img, 0.05)
# 应用不同滤波
mean_filtered = cv2.blur(noisy, (5,5))
median_filtered = cv2.medianBlur(noisy, 5)
bilateral_filtered = cv2.bilateralFilter(noisy, 9, 30, 10)
# 可视化结果
fig, axes = plt.subplots(2, 3, figsize=(15, 10))
images = [img, noisy, mean_filtered,
median_filtered, bilateral_filtered]
titles = ['原始图像', '加噪图像', '均值滤波',
'中值滤波', '双边滤波']
for i, (ax, img, title) in enumerate(zip(axes.flat, images, titles)):
ax.imshow(img, cmap='gray')
ax.set_title(title)
ax.axis('off')
plt.tight_layout()
plt.show()