目录

1.摘要
本文聚焦灾后应急物流的高效与公平配送问题,基于灾情严重程度提出优先分区策略,利用聚类算法将灾区划分为紧急区和次紧急区。在此基础上,本文构建了一个兼顾运营成本最小化与最大短缺率最小化的扩展目标规划模型,用于优化灾后三层应急物流供应链决策。模型同时引入公平性约束与无人机--卡车混合运输模式,以提升灾区物资配送的灵活性与效率。通过 2008 年汶川地震案例验证了模型的有效性,并结合敏感性分析评估关键参数对最优解与系统性能的影响,表明该模型具有良好的鲁棒性和现实适用性。
2.灾区紧急分类
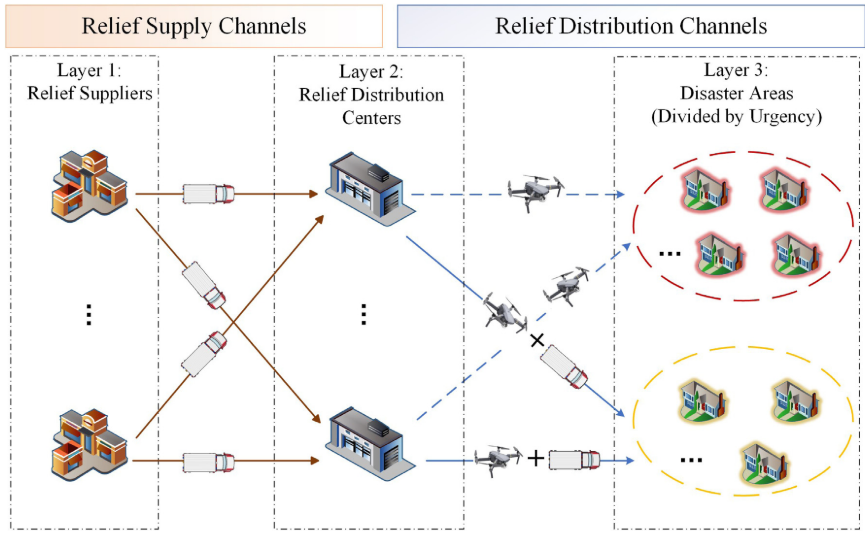
本文构建了一个由救援物资供应商---配送中心---灾区组成的三层应急物流网络,目标是在动态需求环境下最小化总体运营成本并降低最大物资短缺率。灾区根据受灾严重程度被划分为紧急区与次紧急区,其中紧急区优先获得救援资源配置。灾情紧急程度的评估基于多指标综合判定,以适应不同灾害类型的特性。在运输层面,引入无人机--卡车混合运输模式:紧急区优先采用无人机配送以满足时效性需求,次紧急区由剩余无人机与卡车协同服务,从而实现资源的高效与公平分配。为实现灾区优先级的科学划分,本文采用 K-means 聚类算法对灾区进行分级,并据此计算群组优先级参数,为后续救援调度与优化决策提供依据。
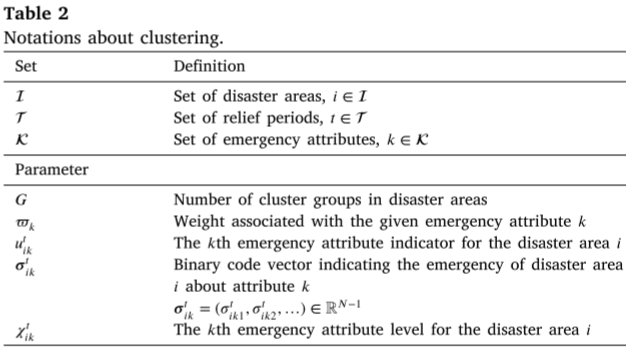
基于多指标应急属性,本文采用 K-means 聚类算法对灾区进行优先级分组。通过属性标准化与群组评价指标计算灾区紧迫度,并据此确定群组优先级参数,最终将灾区划分为紧急区与次紧急区,为应急物资分配提供快速、量化的决策依据。

3.无人机-卡车混合运输模型
本文提出若干基本假设:灾区位置、距离、需求量及灾情均已知;可用于应急调度的无人机与卡车数量为服从联合分布的随机变量;参与配送的均为大型无人机,且其飞行范围不受续航限制约束。基于应急管理领域的常见做法,本文将灾区需求视为已知的确定性需求。
目标函数
在所构建的多配送中心---多灾区应急物流网络中,救援物资按照灾区组优先级进行分配。
F 1 ( x r m i t , y r m i t , y ~ r m i t , z r s m t ) = ∑ t ∈ T [ λ 1 t ∑ r ∈ R ∑ m ∈ M ∑ i ∈ I 1 ( V r b i t + C ~ D m i ↓ ) y ~ r m i t ] + λ 2 t ∑ r ∈ R ∑ m ∈ M ∑ i ∈ I 2 ( V r b i t x r m i t + C ~ D m i ↓ y ~ r m i t + C D m i ↓ y r m i t ) + ∑ r ∈ R ∑ m ∈ M ∑ s ∈ S ( U r + C D m s ↑ ) z r s m t \begin{aligned}F_1(x_{rmi}^t,y_{rmi}^t,\tilde{y}{rmi}^t,z{rsm}^t)&=\sum_{t\in\mathcal{T}}\left[\lambda_{1}^{t}\sum_{r\in\mathcal{R}}\sum_{m\in\mathcal{M}}\sum_{i\in\mathcal{I}{1}}\left(V{r}b_{i}^{t}+\tilde{C}D_{mi}^{\downarrow}\right)\tilde{y}{rmi}^{t}\right]\\&+\lambda{2}^{t}\sum_{r\in R}\sum_{m\in\mathcal{M}}\sum_{i\in\mathcal{I}{2}}\left(V{r}b_{i}^{t}x_{rmi}^{t}+\tilde{C}D_{mi}^{\downarrow}\tilde{y}{rmi}^{t}+CD{mi}^{\downarrow}y_{rmi}^{t}\right)\\&+\sum_{r\in\mathcal{R}}\sum_{m\in\mathcal{M}}\sum_{s\in S}\left(U_{r}+CD_{ms}^{\uparrow}\right)z_{rsm}^{t}\end{aligned} F1(xrmit,yrmit,y~rmit,zrsmt)=t∈T∑[λ1tr∈R∑m∈M∑i∈I1∑(Vrbit+C~Dmi↓)y~rmit]+λ2tr∈R∑m∈M∑i∈I2∑(Vrbitxrmit+C~Dmi↓y~rmit+CDmi↓yrmit)+r∈R∑m∈M∑s∈S∑(Ur+CDms↑)zrsmt
其中, λ t 1 \lambda_t^1 λt1和 λ t 2 \lambda_t^2 λt2 分别表示紧急区与次紧急区的应急权重。目标函数的第一部分用于刻画总运营成本,包括配送中心与供应商的物资配置成本,以及供应商至配送中心、配送中心至灾区的运输成本,并通过权重体现不同灾区组的优先级差异。
F 2 ( x r m i t ) = ∑ t ∈ T ∑ r ∈ R max i { θ r i ( 1 − ∑ m ∈ M x r m i t Q r i t ) } F_{2}(x_{rmi}^{t})=\sum_{t\in\mathcal{T}}\sum_{r\in\mathcal{R}}\max_{i}\left\{\theta_{ri}\left(1-\frac{\sum_{m\in\mathcal{M}}x_{rmi}^{t}}{Q_{ri}^{t}}\right)\right\} F2(xrmit)=t∈T∑r∈R∑imax{θri(1−Qrit∑m∈Mxrmit)}
第二部分用于控制加权最大物资短缺率,以保障救援物资的高效分配。
4.实际操作与讨论
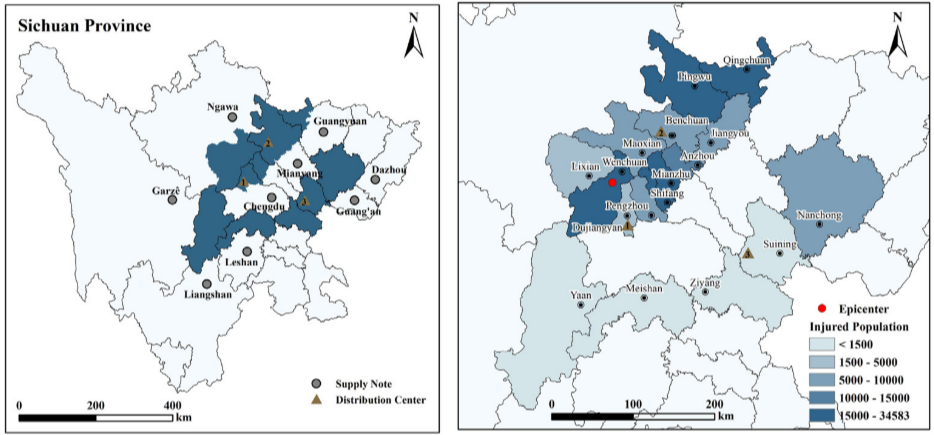
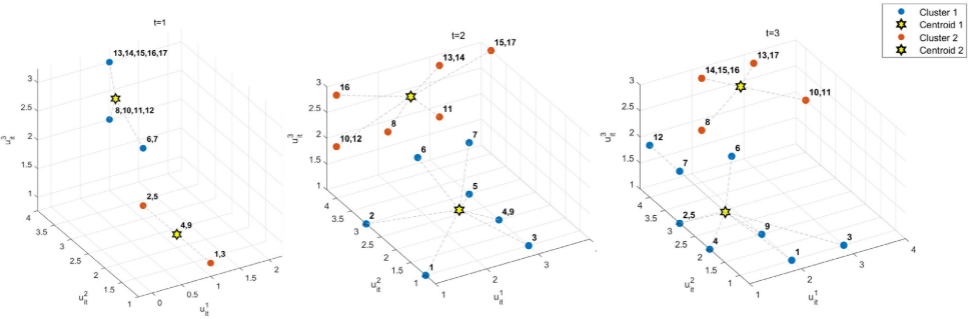
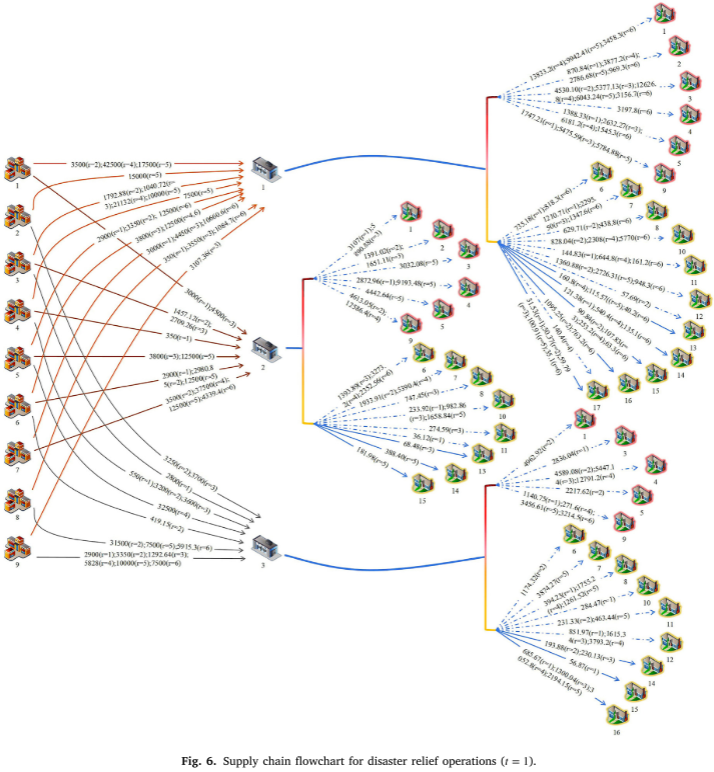
案例中采用无人机与卡车协同运输,区分耐用品与消耗品两类物资,并在寒冷条件下提高耐用品的重要性权重。基于灾区位置、受灾程度及供应网络信息,构建了简化的应急物流网络,对模型在大规模灾害快速响应场景下的可行性与实用性进行了验证。
5.参考文献
1\] Sun J, Lin G H, Zhu X. A hybrid drone-truck model for fair and efficient emergency relief distribution\[J\]. Computers \& Industrial Engineering, 2025: 111607. ### 6.代码获取 xx ### 7.算法辅导·应用定制·读者交流 xx