【机器学习】深度神经网络（DNN）

定义：DNN 是由输入层、多层隐藏层（通常 ≥2 层）和输出层组成的全连接神经网络，层与层之间通过权重矩阵连接，每个神经元通过激活函数引入非线性，最终实现从输入到输出的复杂映射。
核心本质 ：分层特征学习------ 底层隐藏层学习数据的低级特征（如图像的边缘、纹理，文本的字符 / 词语向量），上层隐藏层逐步将低级特征组合为高级语义特征（如图像的物体部件、文本的语义意图），最终通过输出层完成分类、回归等任务。
与浅层网络的区别 ：
- 浅层网络（如单隐藏层感知机）仅能学习线性可分或简单非线性关系；
- DNN 通过多层堆叠，可拟合任意复杂的非线性函数（万能逼近定理），但需解决梯度消失 / 爆炸等训练难题。

三、DNN 网络结构详解

DNN 的结构呈 "全连接" 层级结构，每一层的神经元与下一层的所有神经元完全连接，核心组件包括输入层、隐藏层、输出层、激活函数、权重 / 偏置。

1. 各层组件功能

层级	功能描述	结构细节
输入层	接收原始数据（如特征向量、图像像素、文本嵌入），将数据转换为模型可处理的张量	神经元数量 = 输入数据维度（例：MNIST 图像展平后为 784 维，输入层神经元数 = 784）
隐藏层	学习数据的抽象特征，层数和神经元数是核心超参数	层数越多、神经元数越多，模型表达能力越强，但易过拟合；通常采用 "递减式" 设计（如 784→512→256→128）
输出层	输出任务结果（分类 / 回归 / 生成），神经元数量与任务类型匹配	二分类：1 个神经元（sigmoid 激活）；多分类：N 个神经元（softmax 激活）；回归：1 个神经元（无激活）

2. 核心组件：激活函数

激活函数是 DNN 引入非线性的关键（无激活函数时，多层网络等价于单层线性模型），常用激活函数对比：

激活函数	优点	缺点	适用场景
Sigmoid	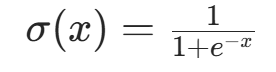输出在 [0,1] 之间，可表示概率	梯度消失（x 过大 / 过小时导数接近 0）	二分类输出层
Tanh	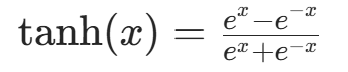输出在 [-1,1] 之间，均值为 0	仍存在梯度消失问题	早期隐藏层（现已少用）
ReLU	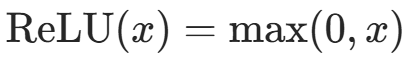计算简单，缓解梯度消失，训练稳定	死亡 ReLU（x<0 时梯度为 0，神经元失效）	隐藏层（最常用）
Leaky ReLU	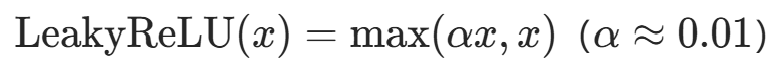解决死亡 ReLU 问题	超参数 α 需调优	隐藏层（ReLU 替代方案）
Softmax	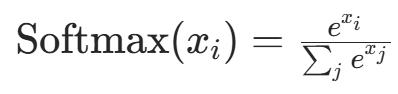输出多分类概率分布，和为 1	计算时需注意数值稳定性（避免溢出）	多分类输出层

3. 权重与偏置

权重（W）：层间连接的参数，决定前一层神经元对后一层的影响强度，初始化为随机小值（如正态分布 N(0,0.01)），避免激活函数饱和。
偏置（b）：每个神经元的偏移量，用于调整激活函数的输入阈值，初始化为 0 或小值。

四、DNN 核心训练原理

DNN 的训练目标是通过反向传播（Backpropagation, BP）算法 最小化损失函数，找到最优的权重和偏置。训练流程分为两大步：前向传播（计算预测值） 和 反向传播（更新参数）。

1. 第一步：前向传播（Forward Propagation）

从输入层到输出层逐层计算神经元的激活值，最终得到预测结果。以含 1 个隐藏层的 DNN 为例（输入层 x，隐藏层 h，输出层）：

隐藏层激活值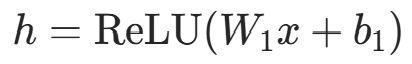：（为输入层→隐藏层权重，为隐藏层偏置）
输出层预测值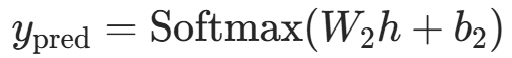：（为隐藏层→输出层权重，为输出层偏置）

2. 第二步：反向传播（Backpropagation）

通过链式法则计算损失函数对各层权重和偏置的梯度，再用优化器更新参数，核心是 "误差反向传播"。

（1）损失函数选择

分类任务：交叉熵损失（Cross-Entropy Loss）------ 适合概率分布类预测

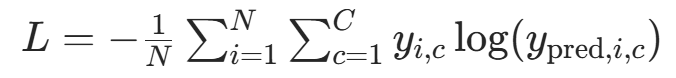
（为真实标签的独热编码，为预测概率）

回归任务：均方误差（MSE）------ 适合连续值预测

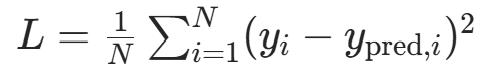
（2）梯度计算与参数更新

计算输出层误差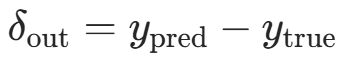：（交叉熵损失下简化结果）
反向传播隐藏层误差：（⊙ 为元素积，ReLU′ 为激活函数导数）
计算梯度：

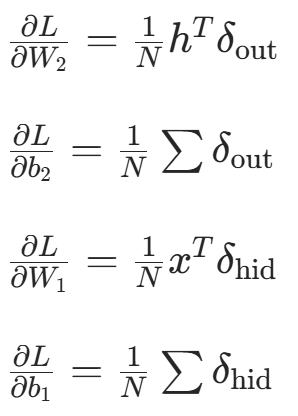
参数更新（以 SGD 优化器为例）：

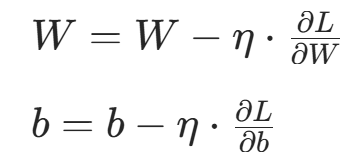
（η 为学习率，控制步长）

3. 训练关键问题与解决方案

（1）梯度消失 / 爆炸

问题：深层网络中，梯度通过链式法则传播时，会因激活函数导数小于 1（如 sigmoid 导数最大 0.25）而指数级衰减（梯度消失），或因权重过大而指数级增长（梯度爆炸）。
解决方案 ：
- 激活函数：用 ReLU 替代 sigmoid/tanh；
- 权重初始化：Xavier 初始化（适配 tanh）、He 初始化（适配 ReLU）；
- 批量归一化（Batch Normalization, BN）：对每层输入标准化，稳定梯度；
- 残差连接（Residual Connection）：跳过部分层，直接传递梯度（如 ResNet）。

（2）过拟合

问题：模型在训练集上表现好，测试集上泛化能力差。
解决方案 ：
- 正则化：L1 正则化（权重稀疏）、L2 正则化（权重衰减）；
- Dropout：训练时随机失活部分神经元，防止过度依赖；
- 早停（Early Stopping）：监控验证集损失，停止过早过拟合；
- 数据增强：增加训练数据多样性（如图像翻转、裁剪）。

（3）优化器选择

优化器	核心特点	学习率建议	适用场景
SGD	基础优化器，收敛稳定但速度慢	η=0.01∼0.1	简单任务、需精细调参
Adam	结合动量和自适应学习率，收敛快且稳定	η=0.001	复杂任务、快速迭代（首选）
RMSprop	自适应学习率，适合非平稳目标函数	η=0.001	语音、NLP 等序列任务

五、DNN 的典型应用场景

DNN 凭借强大的非线性拟合能力，广泛应用于各类复杂任务，核心场景包括：

图像识别与分类：如 MNIST 手写数字识别、CIFAR-10 物体分类（基础 DNN），复杂场景需结合 CNN（如 ResNet、ViT）；
自然语言处理（NLP）：文本分类（情感分析、垃圾邮件检测）、命名实体识别、文本生成（基础 DNN 需结合词嵌入，复杂场景用 Transformer）；
语音识别与合成：语音转文字（ASR）、文字转语音（TTS），需结合 RNN/CNN 处理时序特征；
推荐系统：用户 - 物品评分预测、个性化推荐（如协同过滤中的矩阵分解可通过 DNN 实现）；
回归预测：房价预测、股票价格预测、销量预测等连续值预测任务；
异常检测：欺诈交易检测、设备故障诊断（学习正常数据分布，识别偏离分布的异常）。

六、基于深度神经网络（DNN）的Python代码完整实现

python 复制代码

import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, Dataset
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from tqdm import tqdm
from sklearn.metrics import confusion_matrix, classification_report
import warnings
from scipy.ndimage import gaussian_filter1d  # 用于滑动平均

warnings.filterwarnings('ignore')

# 设置绘图风格
plt.rcParams['font.sans-serif'] = ['DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
sns.set_style("whitegrid")
plt.rcParams['figure.figsize'] = (12, 8)


# -------------------------- 1. 通用合成分类数据集 --------------------------
class SyntheticClassificationDataset(Dataset):
    def __init__(self, num_samples=10000, feature_dim=32, num_classes=10, train=True):
        self.num_samples = num_samples
        self.feature_dim = feature_dim
        self.num_classes = num_classes

        # 生成带标签相关性的特征（避免随机数据导致准确率过低）
        self.features = torch.randn(num_samples, feature_dim)
        # 让特征与标签存在弱相关性（更贴近真实数据）
        self.labels = torch.randint(0, num_classes, (num_samples,))
        for i in range(num_samples):
            self.features[i] += self.labels[i] * 0.5  # 标签对特征添加偏移

        # 划分训练/测试集
        split_idx = int(num_samples * 0.8)
        if train:
            self.features = self.features[:split_idx]
            self.labels = self.labels[:split_idx]
        else:
            self.features = self.features[split_idx:]
            self.labels = self.labels[split_idx:]

    def __len__(self):
        return len(self.features)

    def __getitem__(self, idx):
        return self.features[idx], self.labels[idx]


# -------------------------- 2. 定义 DNN 模型 --------------------------
class DNN(nn.Module):
    def __init__(self, input_dim, hidden_dims, output_dim, dropout_rate=0.2):
        super(DNN, self).__init__()
        self.input_dim = input_dim
        self.hidden_dims = hidden_dims
        self.output_dim = output_dim
        self.dropout_rate = dropout_rate

        # 构建隐藏层（拆分层以便记录激活值）
        self.layers = nn.ModuleList()
        self.bn_layers = nn.ModuleList()
        self.dropout_layers = nn.ModuleList()

        prev_dim = input_dim
        for hidden_dim in hidden_dims:
            self.layers.append(nn.Linear(prev_dim, hidden_dim))
            self.bn_layers.append(nn.BatchNorm1d(hidden_dim))
            self.dropout_layers.append(nn.Dropout(dropout_rate))
            prev_dim = hidden_dim

        # 输出层
        self.output_layer = nn.Sequential(
            nn.Linear(prev_dim, output_dim),
            nn.Softmax(dim=1)
        )

        # 记录训练指标
        self.train_losses = []
        self.test_losses = []
        self.train_accs = []
        self.test_accs = []
        # 记录隐藏层激活值（最后一次前向传播）
        self.hidden_activations = []
        # 保存输入特征（用于分布可视化）
        self.input_features = None

    def forward(self, x, record_activations=False):
        """前向传播：可选记录隐藏层激活值"""
        # 保存输入特征
        if self.input_features is None:
            self.input_features = x.detach().cpu().numpy()

        activations = []
        for i in range(len(self.layers)):
            x = self.layers[i](x)
            x = self.bn_layers[i](x)
            x = nn.functional.relu(x)
            if record_activations:
                activations.append(x.detach().cpu().numpy())
            x = self.dropout_layers[i](x)

        # 记录激活值
        if record_activations:
            self.hidden_activations = activations

        output = self.output_layer(x)
        return output

    def train_model(self, train_loader, test_loader, epochs=50, lr=0.001, device='cuda'):
        """训练模型：包含前向传播、反向传播、参数更新"""
        criterion = nn.CrossEntropyLoss()  # 多分类交叉熵损失
        optimizer = optim.Adam(self.parameters(), lr=lr, weight_decay=1e-4)  # L2 正则化

        print("===== 开始训练 DNN =====")
        for epoch in tqdm(range(epochs), desc="训练进度"):
            # 训练阶段
            self.train()
            train_loss = 0.0
            correct = 0
            total = 0
            for data, targets in train_loader:
                data, targets = data.to(device), targets.to(device)

                # 前向传播
                outputs = self(data)
                loss = criterion(outputs, targets)

                # 反向传播与参数更新
                optimizer.zero_grad()
                loss.backward()
                optimizer.step()

                # 统计训练指标
                train_loss += loss.item() * data.size(0)
                _, predicted = torch.max(outputs, 1)
                total += targets.size(0)
                correct += (predicted == targets).sum().item()

            # 计算训练集指标
            avg_train_loss = train_loss / total
            train_acc = correct / total
            self.train_losses.append(avg_train_loss)
            self.train_accs.append(train_acc)

            # 测试阶段
            self.eval()
            test_loss = 0.0
            correct = 0
            total = 0
            all_preds = []
            all_targets = []
            with torch.no_grad():
                for data, targets in test_loader:
                    data, targets = data.to(device), targets.to(device)
                    # 测试时记录最后一次激活值
                    outputs = self(data, record_activations=(epoch == epochs - 1))
                    loss = criterion(outputs, targets)

                    # 统计测试指标
                    test_loss += loss.item() * data.size(0)
                    _, predicted = torch.max(outputs, 1)
                    total += targets.size(0)
                    correct += (predicted == targets).sum().item()

                    # 保存预测结果（混淆矩阵用）
                    all_preds.extend(predicted.cpu().numpy())
                    all_targets.extend(targets.cpu().numpy())

            # 计算测试集指标
            avg_test_loss = test_loss / total
            test_acc = correct / total
            self.test_losses.append(avg_test_loss)
            self.test_accs.append(test_acc)

            # 打印每轮结果
            tqdm.write(
                f"Epoch {epoch + 1:2d} | "
                f"Train Loss: {avg_train_loss:.4f} | Train Acc: {train_acc:.4f} | "
                f"Test Loss: {avg_test_loss:.4f} | Test Acc: {test_acc:.4f}"
            )

        # 保存混淆矩阵和分类报告
        self.confusion_matrix = confusion_matrix(all_targets, all_preds)
        self.classification_report = classification_report(
            all_targets, all_preds, target_names=[f'Class {i}' for i in range(self.output_dim)],
            output_dict=True
        )
        self.classes = list(range(self.output_dim))
        self.all_preds = all_preds
        self.all_targets = all_targets


# -------------------------- 3. 可视化函数 --------------------------
def plot_training_curves(dnn):
    """绘制训练/测试损失和准确率曲线"""
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))

    # 损失曲线
    epochs = range(1, len(dnn.train_losses) + 1)
    ax1.plot(epochs, dnn.train_losses, marker='o', linewidth=2, label='Train Loss', color='#1f77b4')
    ax1.plot(epochs, dnn.test_losses, marker='s', linewidth=2, label='Test Loss', color='#ff7f0e')
    ax1.set_title('Training & Test Loss vs Epoch', fontsize=14)
    ax1.set_xlabel('Epoch', fontsize=12)
    ax1.set_ylabel('Cross-Entropy Loss', fontsize=12)
    ax1.legend(fontsize=10)
    ax1.grid(True, alpha=0.3)

    # 准确率曲线
    ax2.plot(epochs, dnn.train_accs, marker='o', linewidth=2, label='Train Acc', color='#1f77b4')
    ax2.plot(epochs, dnn.test_accs, marker='s', linewidth=2, label='Test Acc', color='#ff7f0e')
    ax2.set_title('Training & Test Accuracy vs Epoch', fontsize=14)
    ax2.set_xlabel('Epoch', fontsize=12)
    ax2.set_ylabel('Accuracy', fontsize=12)
    ax2.legend(fontsize=10)
    ax2.grid(True, alpha=0.3)

    plt.tight_layout()
    plt.savefig('dnn_training_curves.png', dpi=300, bbox_inches='tight')
    plt.show()


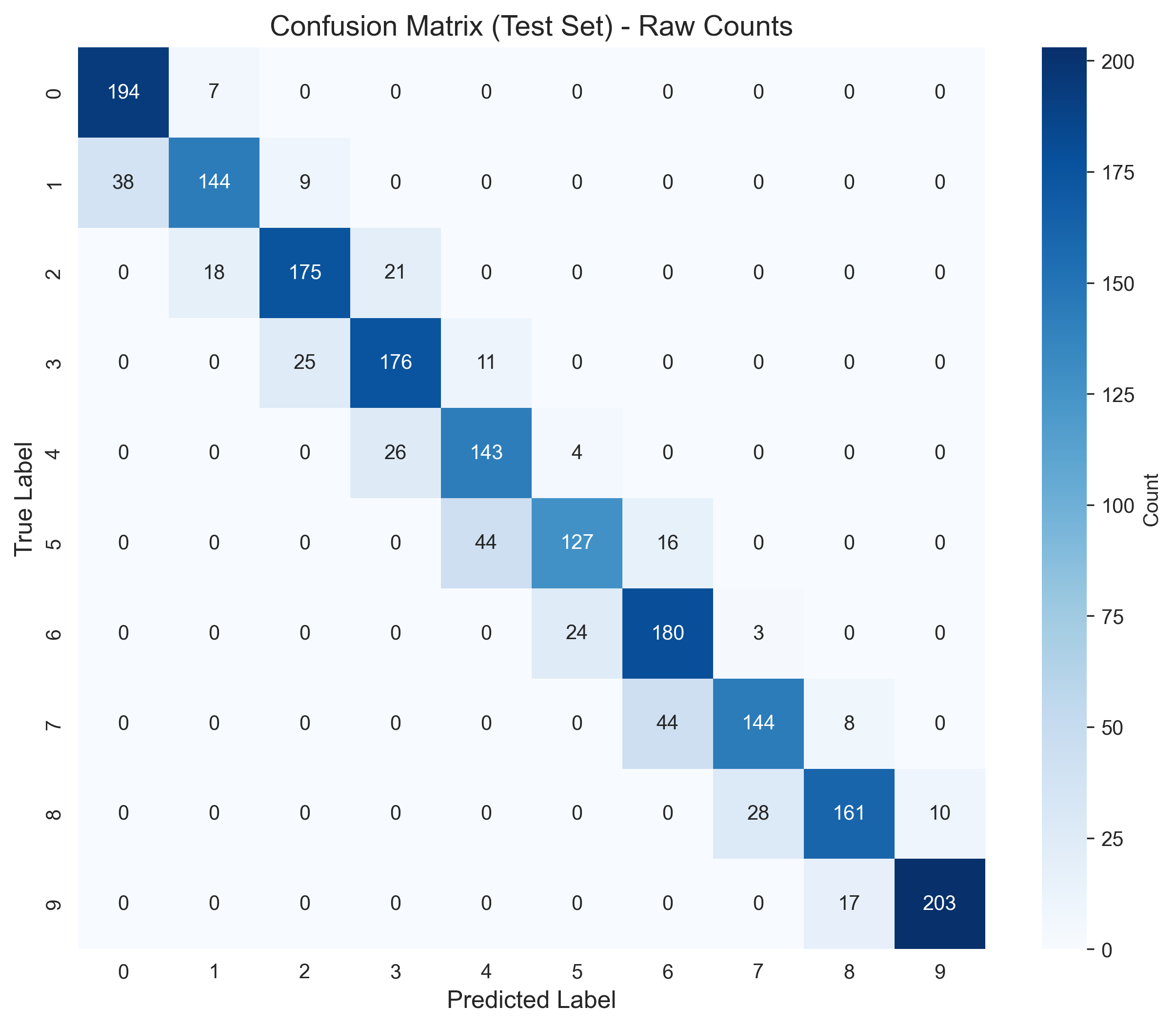
def plot_confusion_matrix(dnn):
    """绘制混淆矩阵（原始计数）"""
    plt.figure(figsize=(10, 8))
    sns.heatmap(
        dnn.confusion_matrix,
        annot=True,
        fmt='d',
        cmap='Blues',
        xticklabels=dnn.classes,
        yticklabels=dnn.classes,
        cbar_kws={'label': 'Count'}
    )
    plt.title('Confusion Matrix (Test Set) - Raw Counts', fontsize=14)
    plt.xlabel('Predicted Label', fontsize=12)
    plt.ylabel('True Label', fontsize=12)
    plt.savefig('dnn_confusion_matrix.png', dpi=300, bbox_inches='tight')
    plt.show()


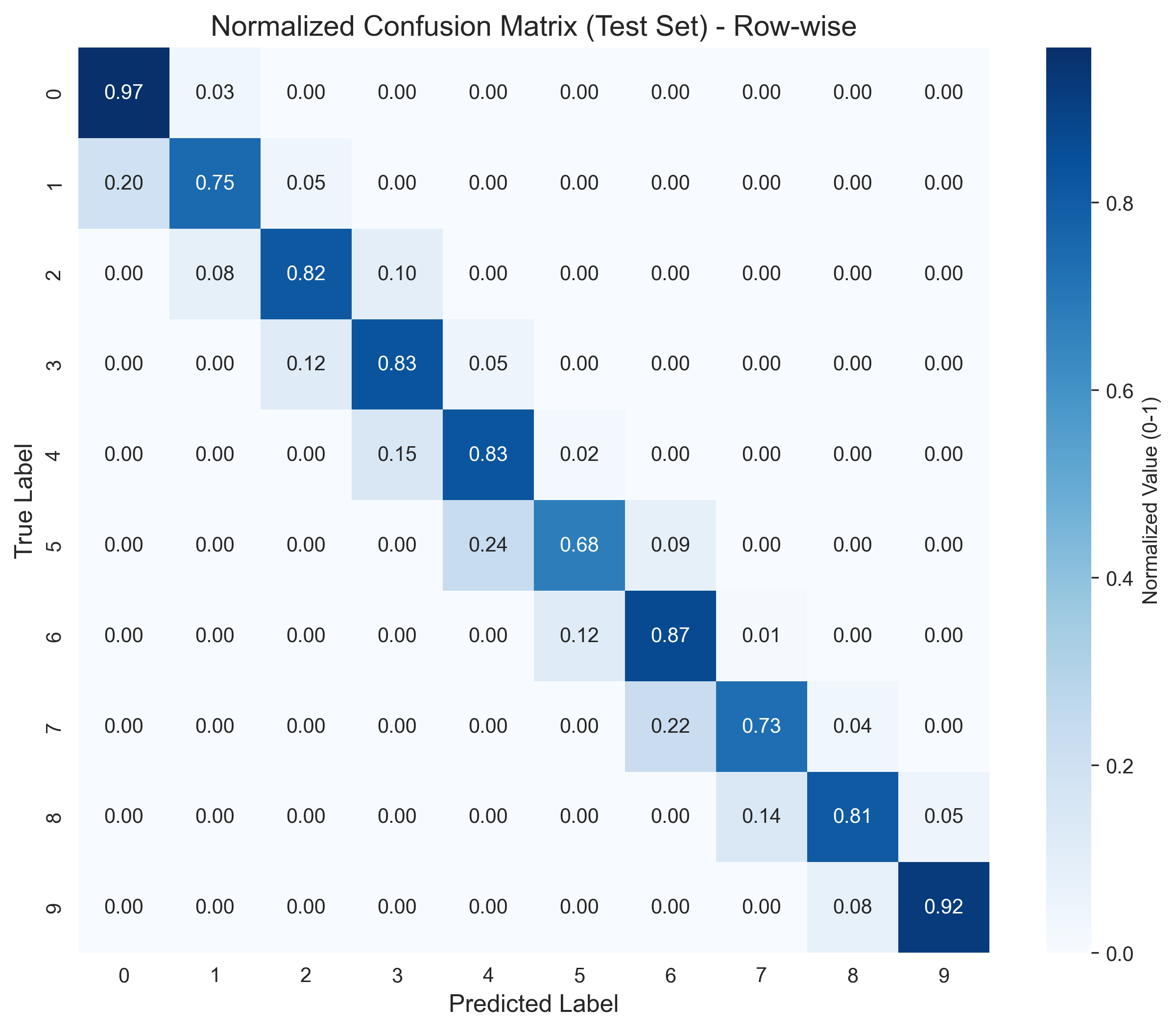
def plot_normalized_confusion_matrix(dnn):
    """绘制归一化混淆矩阵（按行归一化，显示百分比）"""
    cm_normalized = dnn.confusion_matrix.astype('float') / dnn.confusion_matrix.sum(axis=1)[:, np.newaxis]
    plt.figure(figsize=(10, 8))
    sns.heatmap(
        cm_normalized,
        annot=True,
        fmt='.2f',
        cmap='Blues',
        xticklabels=dnn.classes,
        yticklabels=dnn.classes,
        cbar_kws={'label': 'Normalized Value (0-1)'}
    )
    plt.title('Normalized Confusion Matrix (Test Set) - Row-wise', fontsize=14)
    plt.xlabel('Predicted Label', fontsize=12)
    plt.ylabel('True Label', fontsize=12)
    plt.savefig('dnn_normalized_cm.png', dpi=300, bbox_inches='tight')
    plt.show()


def plot_final_metrics(dnn):
    """绘制最终训练/测试指标对比"""
    final_train_acc = dnn.train_accs[-1]
    final_test_acc = dnn.test_accs[-1]
    final_train_loss = dnn.train_losses[-1]
    final_test_loss = dnn.test_losses[-1]

    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))

    # 准确率对比
    acc_data = pd.DataFrame({
        'Type': ['Train Acc', 'Test Acc'],
        'Value': [final_train_acc, final_test_acc]
    })
    sns.barplot(x='Type', y='Value', data=acc_data, palette='Set1', ax=ax1)
    ax1.set_title('Final Accuracy Comparison', fontsize=14)
    ax1.set_ylabel('Accuracy')
    ax1.set_ylim(0, 1)
    ax1.text(0, final_train_acc + 0.02, f'{final_train_acc:.4f}', ha='center', fontsize=12)
    ax1.text(1, final_test_acc + 0.02, f'{final_test_acc:.4f}', ha='center', fontsize=12)
    ax1.grid(True, alpha=0.3, axis='y')

    # 损失对比
    loss_data = pd.DataFrame({
        'Type': ['Train Loss', 'Test Loss'],
        'Value': [final_train_loss, final_test_loss]
    })
    sns.barplot(x='Type', y='Value', data=loss_data, palette='Set2', ax=ax2)
    ax2.set_title('Final Loss Comparison', fontsize=14)
    ax2.set_ylabel('Cross-Entropy Loss')
    ax2.text(0, final_train_loss + 0.02, f'{final_train_loss:.4f}', ha='center', fontsize=12)
    ax2.text(1, final_test_loss + 0.02, f'{final_test_loss:.4f}', ha='center', fontsize=12)
    ax2.grid(True, alpha=0.3, axis='y')

    plt.tight_layout()
    plt.savefig('dnn_final_metrics.png', dpi=300, bbox_inches='tight')
    plt.show()


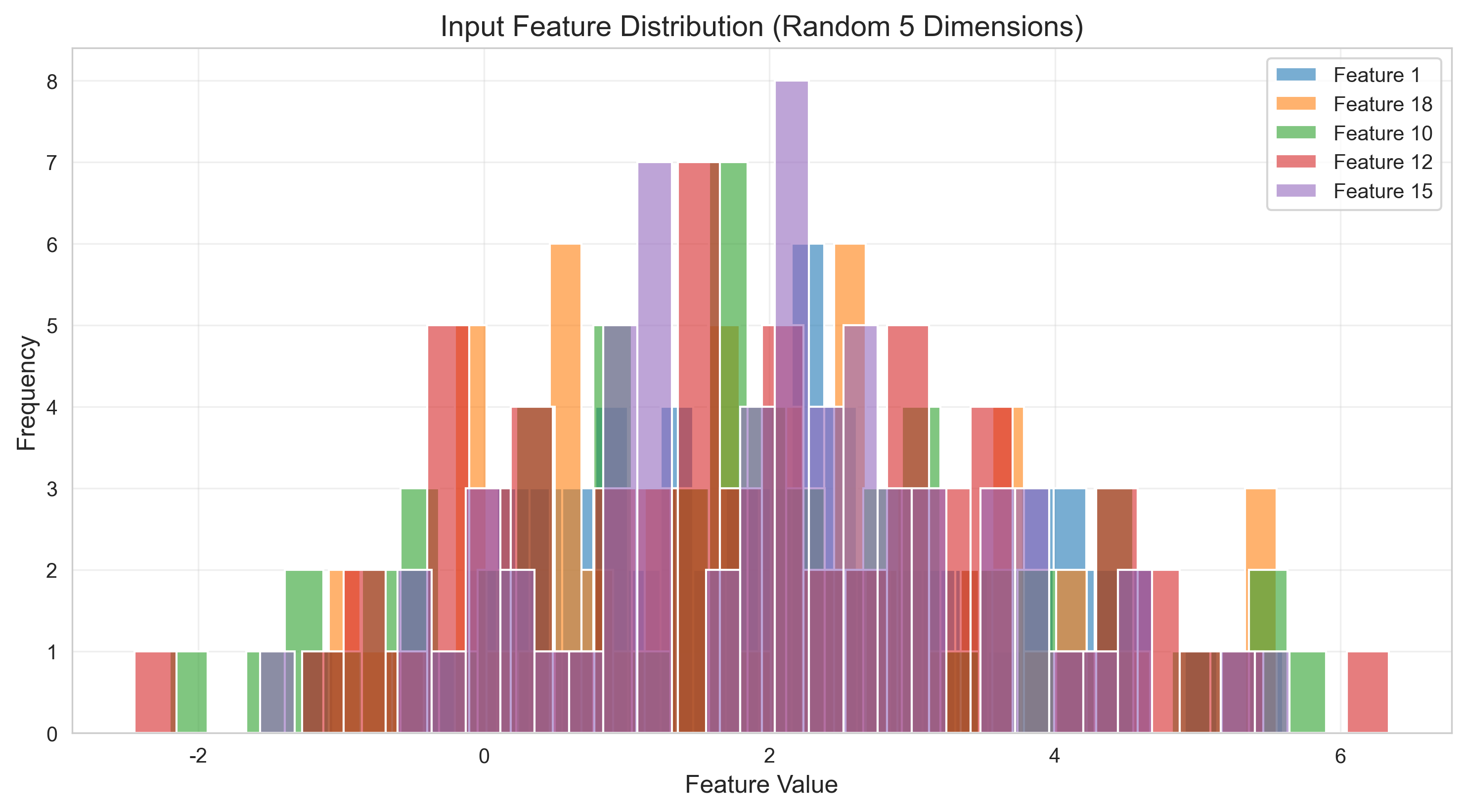
def plot_feature_distribution(dnn):
    """绘制输入特征分布直方图（随机选5个维度）"""
    if dnn.input_features is None:
        print("无输入特征数据！")
        return

    features = dnn.input_features
    plt.figure(figsize=(12, 6))
    # 随机选5个特征维度
    selected_dims = np.random.choice(features.shape[1], 5, replace=False)
    colors = ['#1f77b4', '#ff7f0e', '#2ca02c', '#d62728', '#9467bd']

    for i, dim in enumerate(selected_dims):
        sns.histplot(features[:, dim], bins=30, alpha=0.6, label=f'Feature {dim}', color=colors[i])

    plt.title('Input Feature Distribution (Random 5 Dimensions)', fontsize=14)
    plt.xlabel('Feature Value', fontsize=12)
    plt.ylabel('Frequency', fontsize=12)
    plt.legend(fontsize=10)
    plt.grid(True, alpha=0.3)
    plt.savefig('dnn_feature_distribution.png', dpi=300, bbox_inches='tight')
    plt.show()


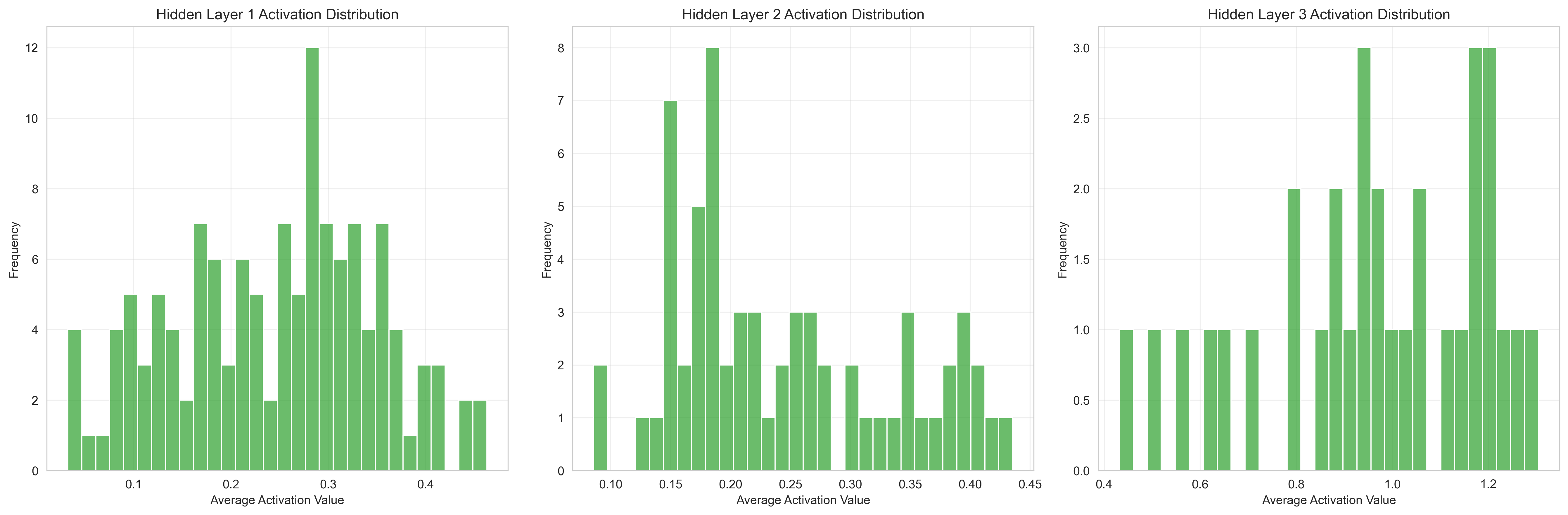
def plot_hidden_activations(dnn):
    """绘制隐藏层激活值分布（每个隐藏层的激活值均值分布）"""
    if not dnn.hidden_activations:
        print("无隐藏层激活值数据！")
        return

    num_layers = len(dnn.hidden_activations)
    fig, axes = plt.subplots(1, num_layers, figsize=(18, 6))
    if num_layers == 1:
        axes = [axes]

    for i, (activations, ax) in enumerate(zip(dnn.hidden_activations, axes)):
        # 计算每个神经元的平均激活值
        avg_activations = np.mean(activations, axis=0)
        sns.histplot(avg_activations, bins=30, color='#2ca02c', alpha=0.7, ax=ax)
        ax.set_title(f'Hidden Layer {i + 1} Activation Distribution', fontsize=12)
        ax.set_xlabel('Average Activation Value', fontsize=10)
        ax.set_ylabel('Frequency', fontsize=10)
        ax.grid(True, alpha=0.3)

    plt.tight_layout()
    plt.savefig('dnn_hidden_activations.png', dpi=300, bbox_inches='tight')
    plt.show()


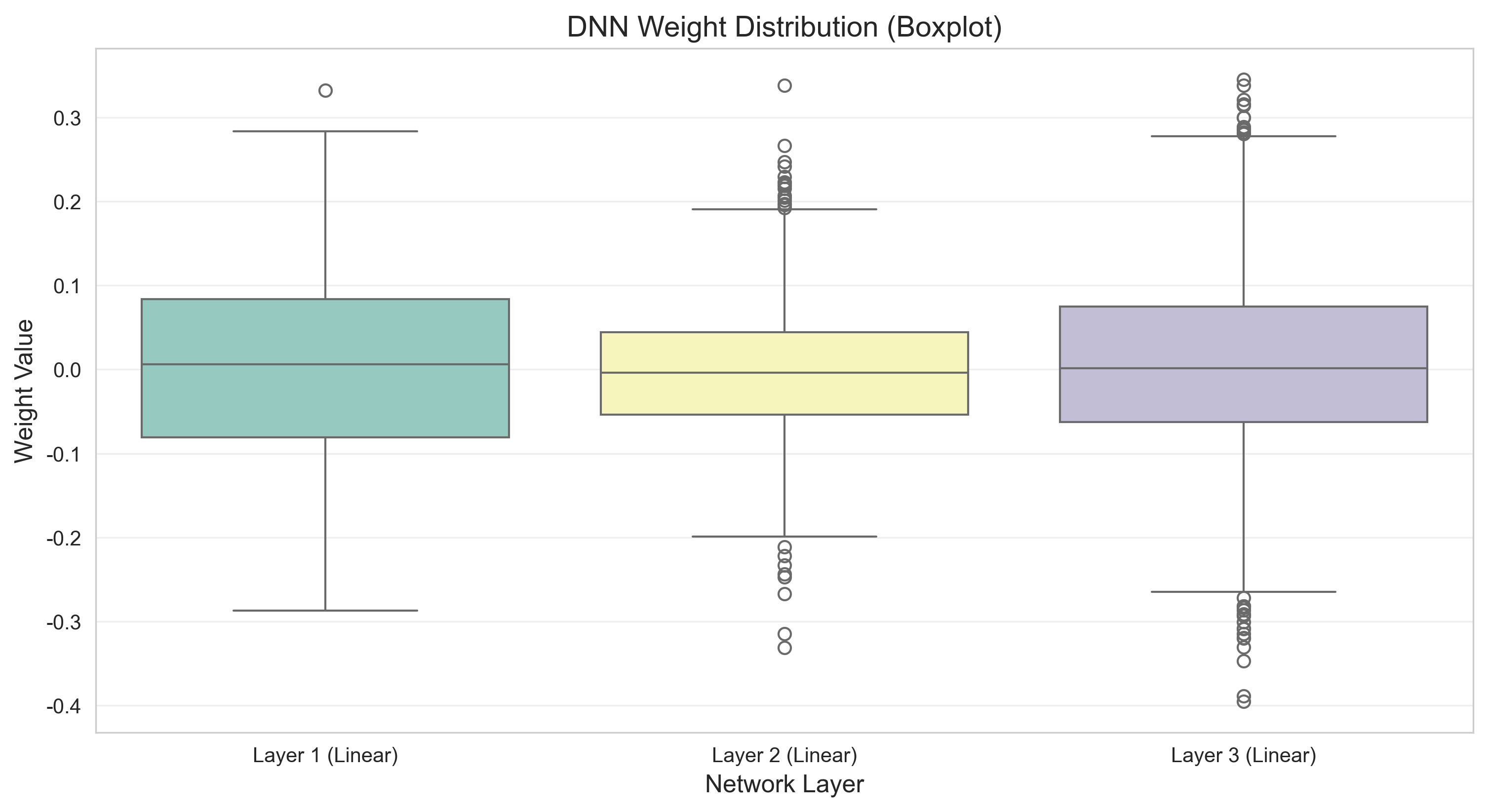
def plot_weight_distribution(dnn):
    """绘制各层权重分布箱线图"""
    weight_data = []
    layer_names = []

    # 收集全连接层权重
    for i, layer in enumerate(dnn.layers):
        weights = layer.weight.detach().cpu().numpy().flatten()
        # 随机采样1000个权重值（避免数据量过大）
        sample_weights = np.random.choice(weights, min(1000, len(weights)), replace=False)
        weight_data.extend(sample_weights)
        layer_names.extend([f'Layer {i + 1} (Linear)' for _ in range(len(sample_weights))])

    # 转为DataFrame
    weight_df = pd.DataFrame({
        'Weight Value': weight_data,
        'Layer': layer_names
    })

    plt.figure(figsize=(12, 6))
    sns.boxplot(x='Layer', y='Weight Value', data=weight_df, palette='Set3')
    plt.title('DNN Weight Distribution (Boxplot)', fontsize=14)
    plt.xlabel('Network Layer', fontsize=12)
    plt.ylabel('Weight Value', fontsize=12)
    plt.grid(True, alpha=0.3, axis='y')
    plt.savefig('dnn_weight_distribution.png', dpi=300, bbox_inches='tight')
    plt.show()


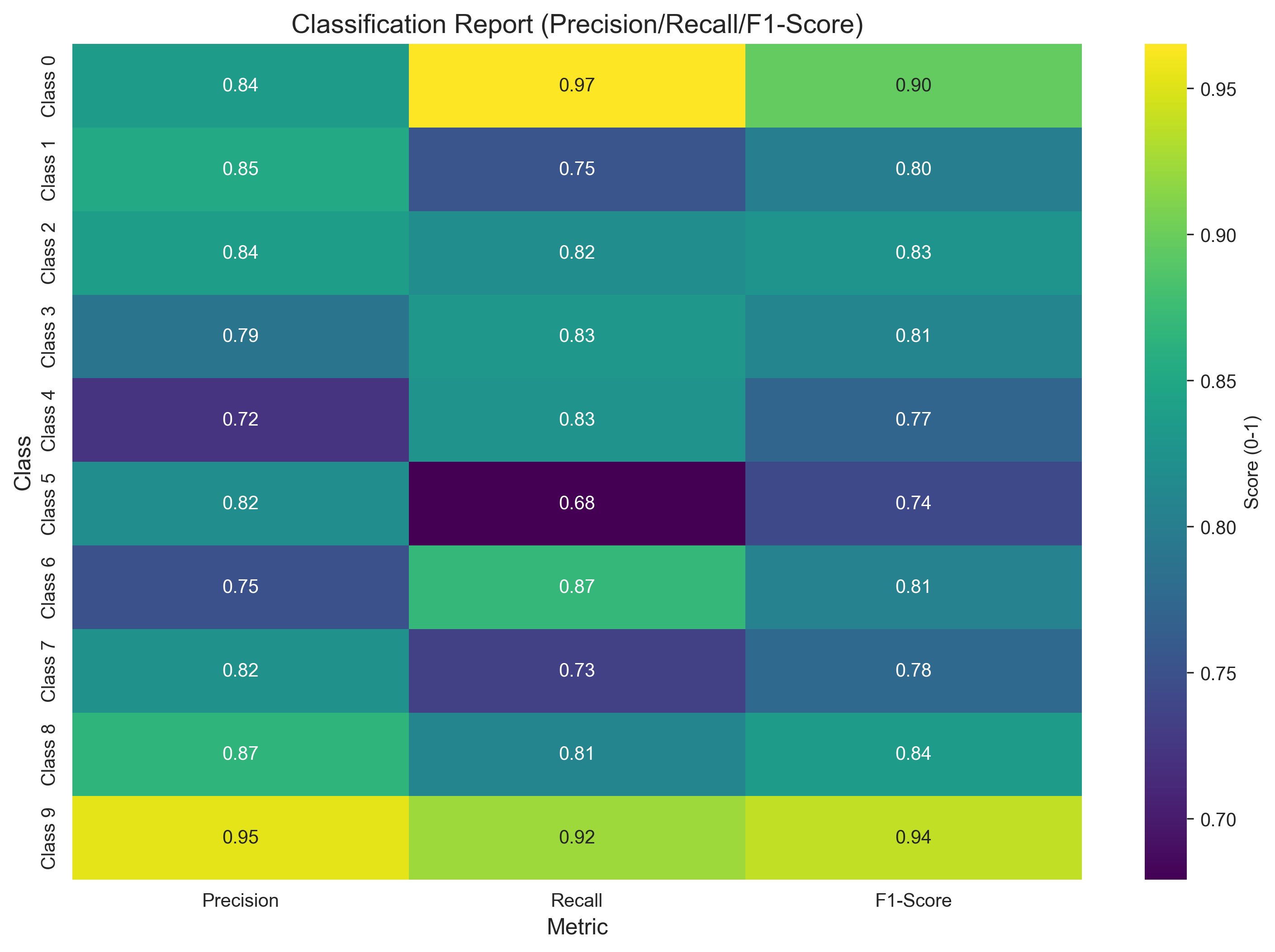
def plot_classification_report(dnn):
    """可视化分类报告（Precision/Recall/F1-Score）"""
    # 提取每类的指标
    class_metrics = []
    classes = []
    for cls in dnn.classes:
        cls_name = f'Class {cls}'
        if cls_name in dnn.classification_report:
            metrics = dnn.classification_report[cls_name]
            class_metrics.append([
                metrics['precision'],
                metrics['recall'],
                metrics['f1-score']
            ])
            classes.append(cls_name)

    # 转为DataFrame
    metrics_df = pd.DataFrame(
        class_metrics,
        columns=['Precision', 'Recall', 'F1-Score'],
        index=classes
    )

    # 绘制热力图
    plt.figure(figsize=(12, 8))
    sns.heatmap(metrics_df, annot=True, fmt='.2f', cmap='viridis', cbar_kws={'label': 'Score (0-1)'})
    plt.title('Classification Report (Precision/Recall/F1-Score)', fontsize=14)
    plt.xlabel('Metric', fontsize=12)
    plt.ylabel('Class', fontsize=12)
    plt.savefig('dnn_classification_report.png', dpi=300, bbox_inches='tight')
    plt.show()

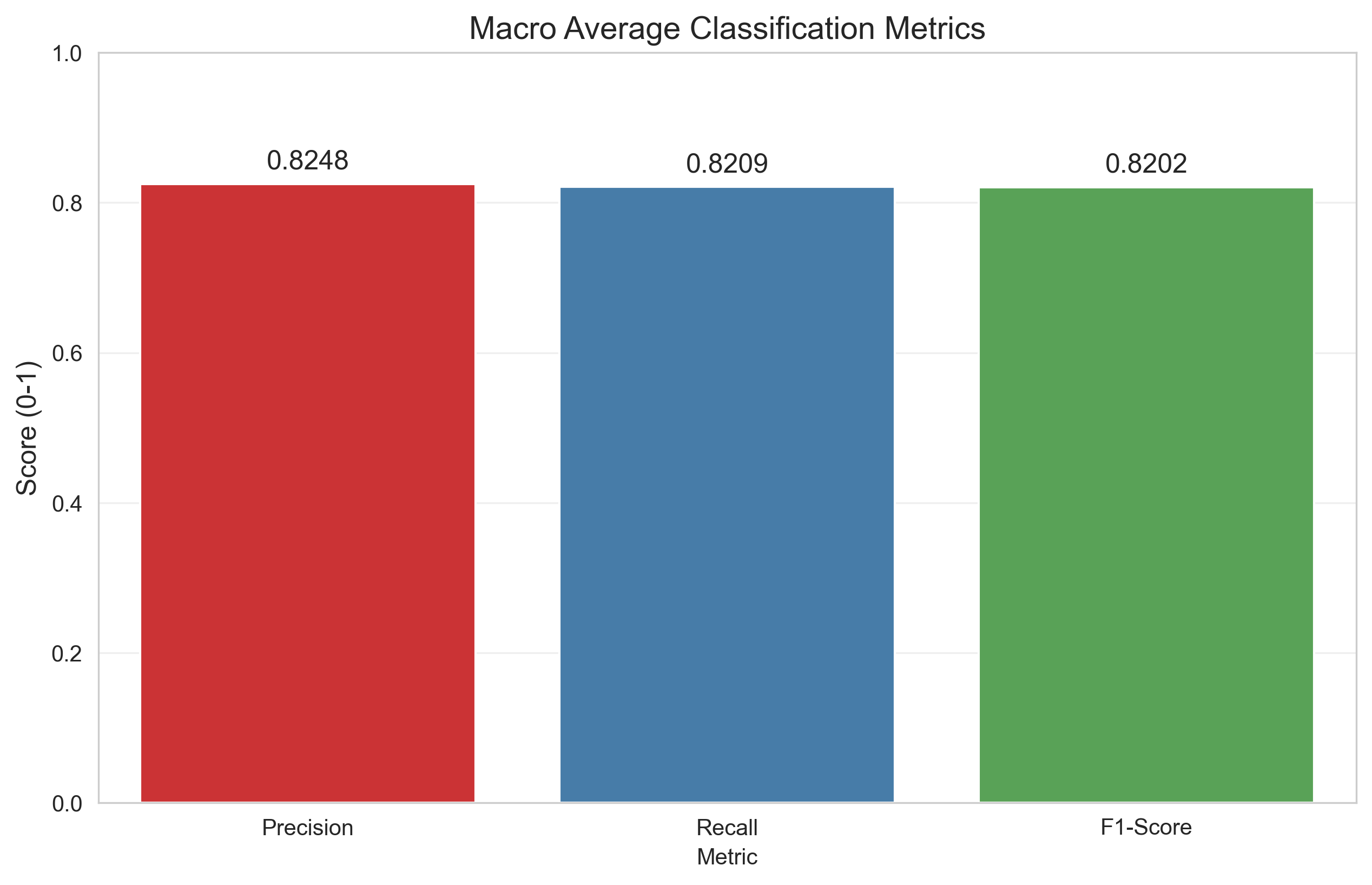
    # 绘制宏观平均指标柱状图
    macro_avg = dnn.classification_report['macro avg']
    macro_data = pd.DataFrame({
        'Metric': ['Precision', 'Recall', 'F1-Score'],
        'Value': [macro_avg['precision'], macro_avg['recall'], macro_avg['f1-score']]
    })

    plt.figure(figsize=(10, 6))
    sns.barplot(x='Metric', y='Value', data=macro_data, palette='Set1')
    plt.title('Macro Average Classification Metrics', fontsize=14)
    plt.ylabel('Score (0-1)', fontsize=12)
    plt.ylim(0, 1)
    for i, val in enumerate(macro_data['Value']):
        plt.text(i, val + 0.02, f'{val:.4f}', ha='center', fontsize=12)
    plt.grid(True, alpha=0.3, axis='y')
    plt.savefig('dnn_macro_metrics.png', dpi=300, bbox_inches='tight')
    plt.show()


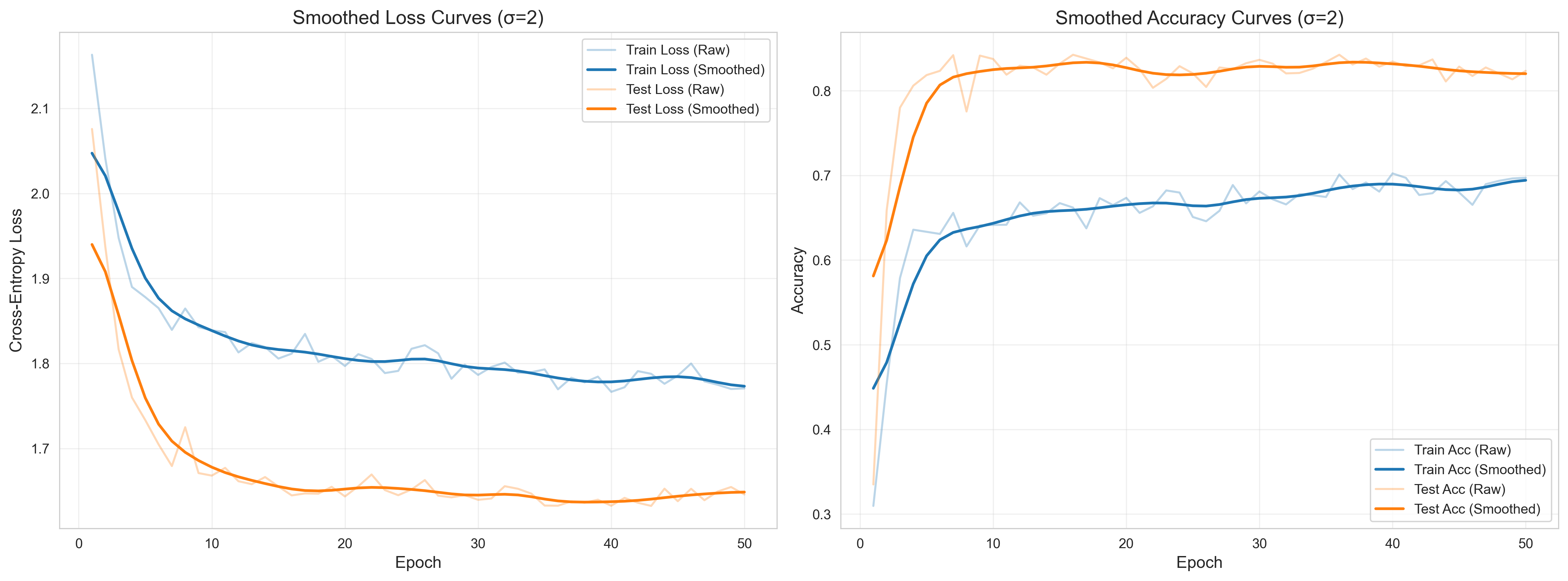
def plot_smooth_curves(dnn, sigma=2):
    """绘制滑动平均后的损失/准确率曲线（更平滑）"""
    # 计算滑动平均
    train_loss_smooth = gaussian_filter1d(dnn.train_losses, sigma=sigma)
    test_loss_smooth = gaussian_filter1d(dnn.test_losses, sigma=sigma)
    train_acc_smooth = gaussian_filter1d(dnn.train_accs, sigma=sigma)
    test_acc_smooth = gaussian_filter1d(dnn.test_accs, sigma=sigma)

    epochs = range(1, len(dnn.train_losses) + 1)
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))

    # 平滑损失曲线
    ax1.plot(epochs, dnn.train_losses, alpha=0.3, color='#1f77b4', label='Train Loss (Raw)')
    ax1.plot(epochs, train_loss_smooth, linewidth=2, color='#1f77b4', label='Train Loss (Smoothed)')
    ax1.plot(epochs, dnn.test_losses, alpha=0.3, color='#ff7f0e', label='Test Loss (Raw)')
    ax1.plot(epochs, test_loss_smooth, linewidth=2, color='#ff7f0e', label='Test Loss (Smoothed)')
    ax1.set_title('Smoothed Loss Curves (σ={})'.format(sigma), fontsize=14)
    ax1.set_xlabel('Epoch', fontsize=12)
    ax1.set_ylabel('Cross-Entropy Loss', fontsize=12)
    ax1.legend(fontsize=10)
    ax1.grid(True, alpha=0.3)

    # 平滑准确率曲线
    ax2.plot(epochs, dnn.train_accs, alpha=0.3, color='#1f77b4', label='Train Acc (Raw)')
    ax2.plot(epochs, train_acc_smooth, linewidth=2, color='#1f77b4', label='Train Acc (Smoothed)')
    ax2.plot(epochs, dnn.test_accs, alpha=0.3, color='#ff7f0e', label='Test Acc (Raw)')
    ax2.plot(epochs, test_acc_smooth, linewidth=2, color='#ff7f0e', label='Test Acc (Smoothed)')
    ax2.set_title('Smoothed Accuracy Curves (σ={})'.format(sigma), fontsize=14)
    ax2.set_xlabel('Epoch', fontsize=12)
    ax2.set_ylabel('Accuracy', fontsize=12)
    ax2.legend(fontsize=10)
    ax2.grid(True, alpha=0.3)

    plt.tight_layout()
    plt.savefig('dnn_smooth_curves.png', dpi=300, bbox_inches='tight')
    plt.show()


def plot_parameter_count(dnn):
    """统计并可视化各层参数数量"""
    param_counts = []
    layer_names = []

    # 统计每一层的参数数量
    for i, layer in enumerate(dnn.layers):
        params = sum(p.numel() for p in layer.parameters())
        param_counts.append(params)
        layer_names.append(f'Hidden Layer {i + 1} (Linear)')

    # 统计BatchNorm层
    for i, bn_layer in enumerate(dnn.bn_layers):
        params = sum(p.numel() for p in bn_layer.parameters())
        param_counts.append(params)
        layer_names.append(f'Hidden Layer {i + 1} (BN)')

    # 统计输出层
    output_params = sum(p.numel() for p in dnn.output_layer.parameters())
    param_counts.append(output_params)
    layer_names.append('Output Layer')

    # 绘制柱状图
    param_df = pd.DataFrame({
        'Layer': layer_names,
        'Parameter Count': param_counts
    })

    plt.figure(figsize=(12, 6))
    sns.barplot(x='Layer', y='Parameter Count', data=param_df, palette='Set3')
    plt.title('DNN Parameter Count per Layer', fontsize=14)
    plt.xlabel('Network Layer', fontsize=12)
    plt.ylabel('Number of Parameters', fontsize=12)
    plt.xticks(rotation=45, ha='right')
    # 标注数值
    for i, val in enumerate(param_counts):
        plt.text(i, val + max(param_counts) * 0.01, f'{val:,}', ha='center', fontsize=10, rotation=0)
    plt.grid(True, alpha=0.3, axis='y')
    plt.tight_layout()
    plt.savefig('dnn_parameter_count.png', dpi=300, bbox_inches='tight')
    plt.show()

    # 总参数数量
    total_params = sum(param_counts)
    print(f"\n模型总参数数量: {total_params:,}")


# -------------------------- 4. 数据加载函数 --------------------------
def load_data(batch_size=64, feature_dim=32, num_classes=10):
    train_dataset = SyntheticClassificationDataset(
        num_samples=10000, feature_dim=feature_dim, num_classes=num_classes, train=True
    )
    test_dataset = SyntheticClassificationDataset(
        num_samples=10000, feature_dim=feature_dim, num_classes=num_classes, train=False
    )

    train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
    test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)
    return train_loader, test_loader


# -------------------------- 5. 主函数 --------------------------
if __name__ == "__main__":
    # 设备配置（自动检测 GPU/CPU）
    device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
    print(f"Using device: {device}")

    # 超参数设置
    feature_dim = 32  # 输入特征维度
    num_classes = 10  # 分类类别数
    hidden_dims = [128, 64, 32]  # 隐藏层维度（3层隐藏层）
    batch_size = 64
    epochs = 50  # 训练轮数
    lr = 0.001  # 学习率
    dropout_rate = 0.2  # Dropout 失活率

    # 1. 加载数据
    train_loader, test_loader = load_data(batch_size, feature_dim, num_classes)

    # 2. 初始化 DNN 模型
    dnn = DNN(
        input_dim=feature_dim,
        hidden_dims=hidden_dims,
        output_dim=num_classes,
        dropout_rate=dropout_rate
    ).to(device)

    # 3. 训练模型
    dnn.train_model(train_loader, test_loader, epochs=epochs, lr=lr, device=device)

    # 4. 保存模型
    torch.save(dnn.state_dict(), "dnn_classification.pth")
    print("\nModel saved as 'dnn_classification.pth'")

    # 5. 可视化训练结果
    print("\n===== 生成可视化图表 =====")
    # 基础可视化
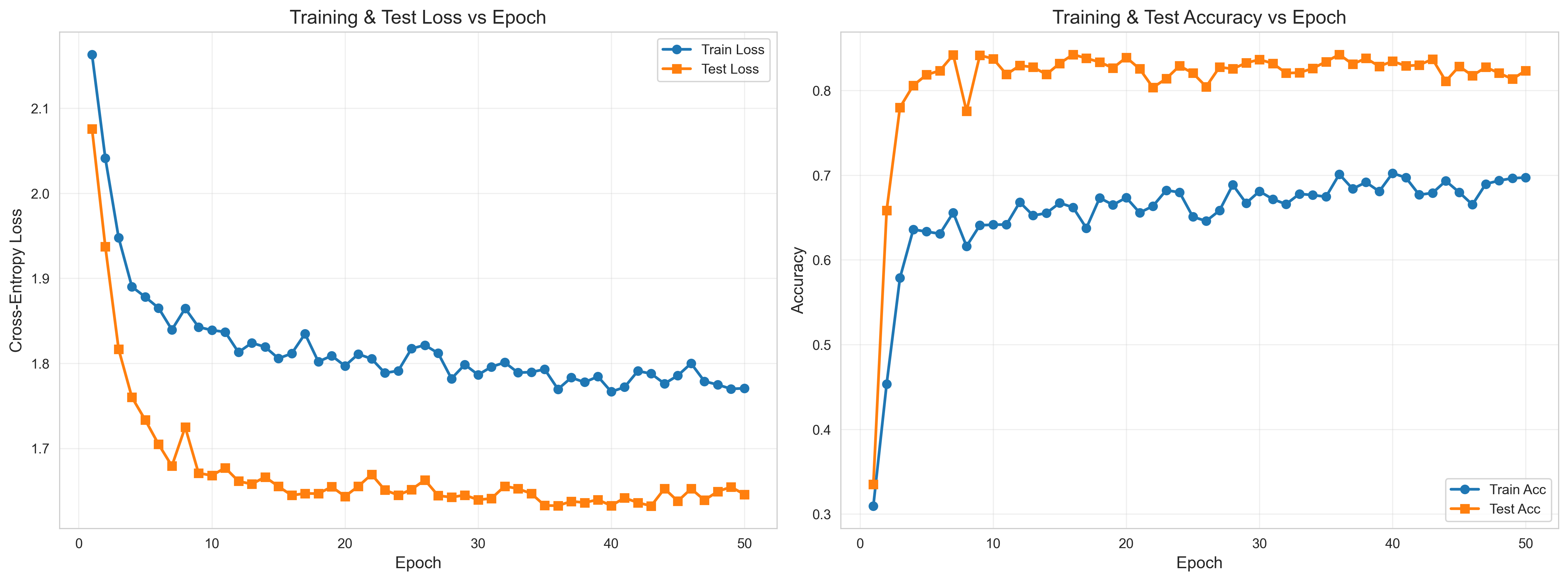
    plot_training_curves(dnn)  # 基础损失/准确率曲线
    plot_confusion_matrix(dnn)  # 原始混淆矩阵
    plot_normalized_confusion_matrix(dnn)  # 归一化混淆矩阵
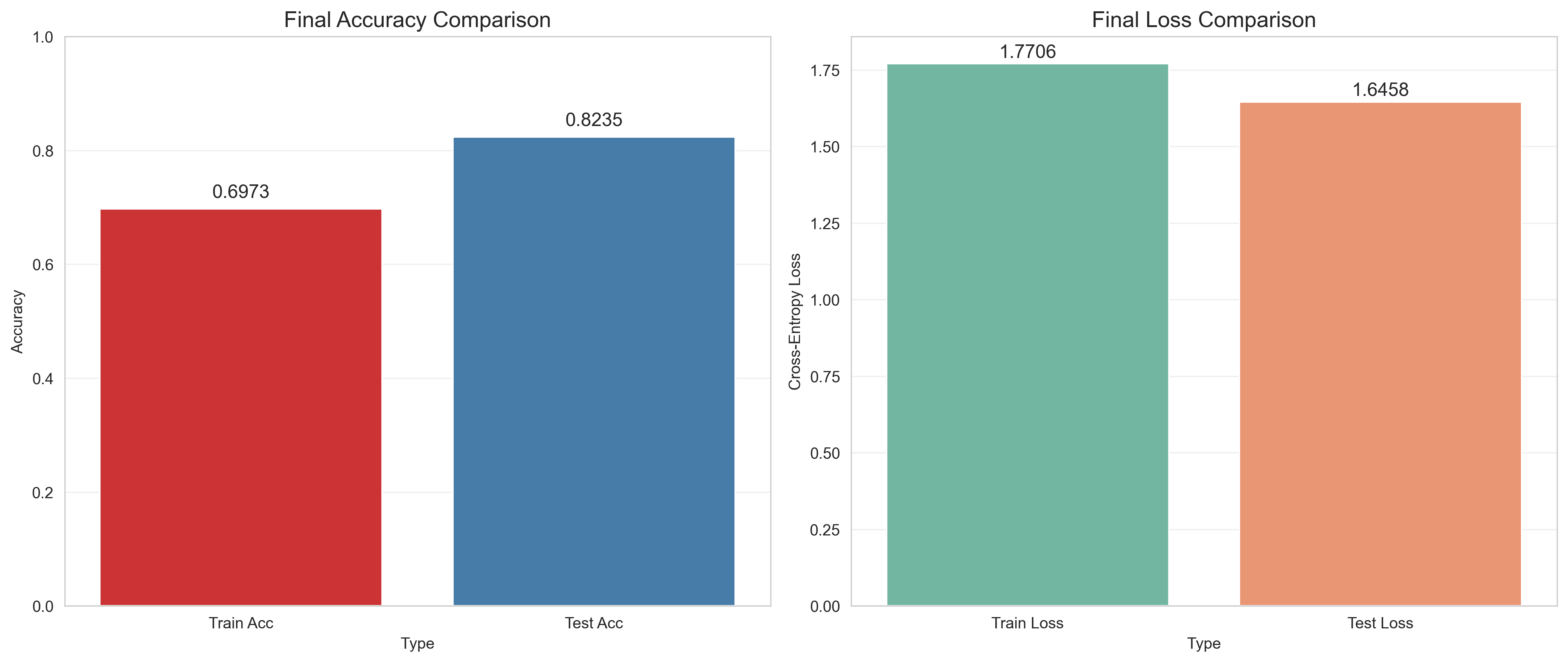
    plot_final_metrics(dnn)  # 最终指标对比
    plot_feature_distribution(dnn)  # 输入特征分布
    plot_hidden_activations(dnn)  # 隐藏层激活值分布
    plot_weight_distribution(dnn)  # 权重分布箱线图
    plot_classification_report(dnn)  # 分类报告（Precision/Recall/F1）
    plot_smooth_curves(dnn, sigma=2)  # 滑动平均曲线
    plot_parameter_count(dnn)  # 各层参数数量统计

    print("\n所有图表已保存到当前目录！")

七、程序运行结果展示

Using device: cpu

===== 开始训练 DNN =====

Epoch 4 | Train Loss: 1.8901 | Train Acc: 0.6359 | Test Loss: 1.7600 | Test Acc: 0.8060

Epoch 7 | Train Loss: 1.8395 | Train Acc: 0.6558 | Test Loss: 1.6793 | Test Acc: 0.8420

Epoch 10 | Train Loss: 1.8390 | Train Acc: 0.6415 | Test Loss: 1.6680 | Test Acc: 0.8375

Epoch 13 | Train Loss: 1.8240 | Train Acc: 0.6524 | Test Loss: 1.6579 | Test Acc: 0.8275

Epoch 15 | Train Loss: 1.8058 | Train Acc: 0.6673 | Test Loss: 1.6552 | Test Acc: 0.8320

Epoch 17 | Train Loss: 1.8347 | Train Acc: 0.6375 | Test Loss: 1.6470 | Test Acc: 0.8380

Epoch 19 | Train Loss: 1.8089 | Train Acc: 0.6650 | Test Loss: 1.6548 | Test Acc: 0.8265

Epoch 23 | Train Loss: 1.7887 | Train Acc: 0.6823 | Test Loss: 1.6509 | Test Acc: 0.8140

Epoch 25 | Train Loss: 1.8173 | Train Acc: 0.6509 | Test Loss: 1.6516 | Test Acc: 0.8205

Epoch 27 | Train Loss: 1.8119 | Train Acc: 0.6583 | Test Loss: 1.6444 | Test Acc: 0.8275

Epoch 30 | Train Loss: 1.7865 | Train Acc: 0.6810 | Test Loss: 1.6395 | Test Acc: 0.8365

Epoch 32 | Train Loss: 1.8010 | Train Acc: 0.6657 | Test Loss: 1.6555 | Test Acc: 0.8205

Epoch 34 | Train Loss: 1.7897 | Train Acc: 0.6766 | Test Loss: 1.6468 | Test Acc: 0.8260

Epoch 36 | Train Loss: 1.7696 | Train Acc: 0.7011 | Test Loss: 1.6325 | Test Acc: 0.8425

Epoch 40 | Train Loss: 1.7666 | Train Acc: 0.7024 | Test Loss: 1.6325 | Test Acc: 0.8345

Epoch 42 | Train Loss: 1.7910 | Train Acc: 0.6769 | Test Loss: 1.6361 | Test Acc: 0.8300

Epoch 44 | Train Loss: 1.7761 | Train Acc: 0.6933 | Test Loss: 1.6526 | Test Acc: 0.8110

Epoch 46 | Train Loss: 1.7999 | Train Acc: 0.6653 | Test Loss: 1.6524 | Test Acc: 0.8175

Epoch 49 | Train Loss: 1.7700 | Train Acc: 0.6964 | Test Loss: 1.6546 | Test Acc: 0.8135

训练进度: 100%|██████████| 50/50 [00:17<00:00, 2.78it/s]

Epoch 50 | Train Loss: 1.7706 | Train Acc: 0.6973 | Test Loss: 1.6458 | Test Acc: 0.8235

Model saved as 'dnn_classification.pth'

===== 生成可视化图表 =====

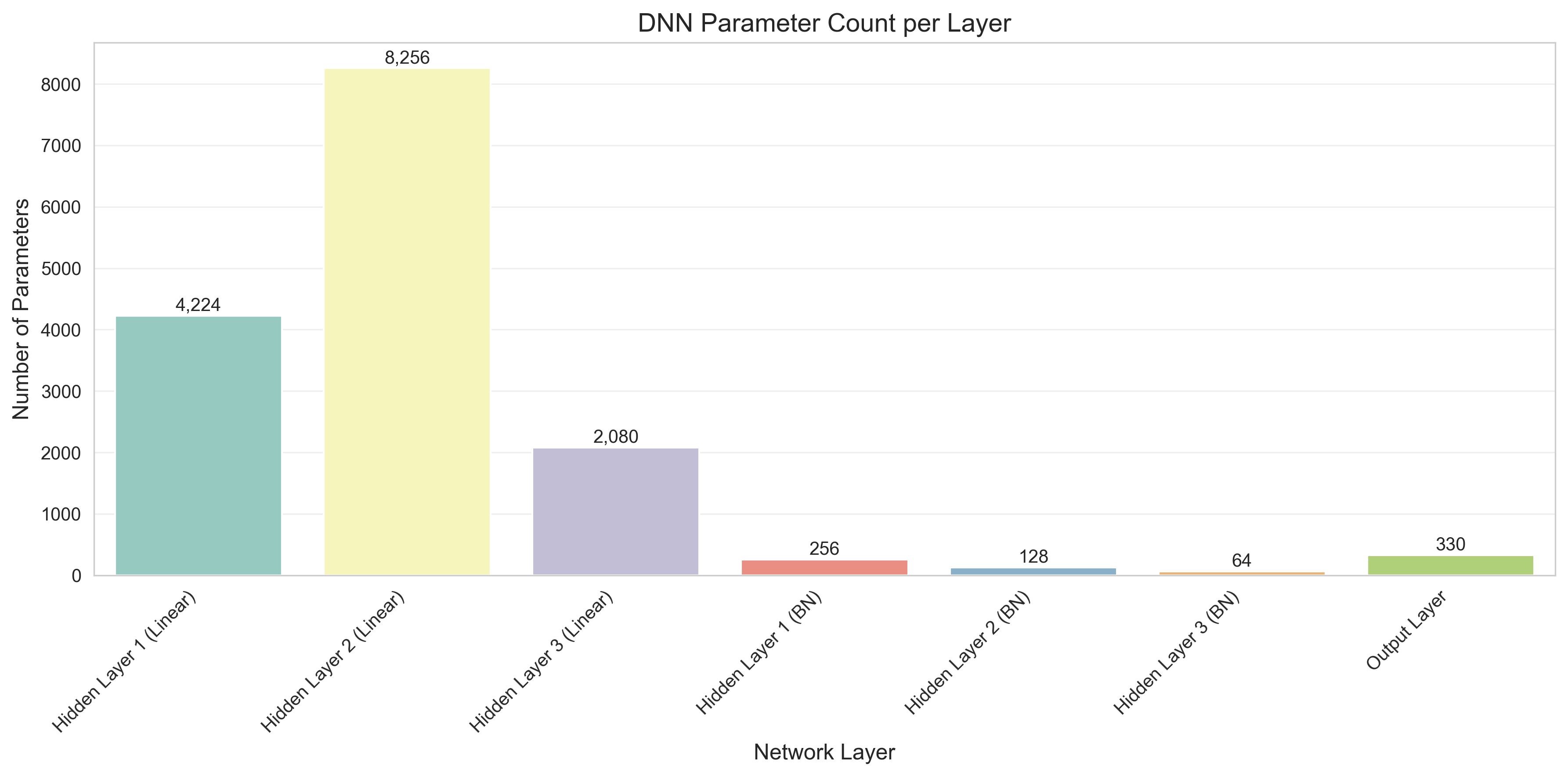
模型总参数数量: 15,338

所有图表已保存到当前目录！

八、DNN 的变体与现代扩展

DNN 是基础框架，针对不同任务场景，衍生出以下核心变体：

卷积神经网络（CNN） ：
- 优化图像 / 网格数据，用卷积层替代全连接层，减少参数并提取局部特征；
- 应用：图像分类、目标检测、语义分割。
循环神经网络（RNN/LSTM/GRU） ：
- 优化序列数据，引入时序依赖（如前一时刻输出作为当前时刻输入）；
- 应用：语音识别、文本生成、机器翻译。
Transformer ：
- 基于自注意力机制，并行计算效率高，捕捉长距离依赖；
- 应用：大语言模型（LLM）、图像生成、多模态任务。
深度残差网络（ResNet） ：
- 引入残差连接，解决深层网络梯度消失问题，可训练上千层；
- 应用：图像识别、超分辨率重建。

九、DNN 实践关键技巧

数据预处理：标准化（StandardScaler）或归一化（MinMaxScaler），避免特征尺度差异导致训练不稳定；
超参数调优 ：
- 隐藏层：层数 2~5 层（过多易过拟合），神经元数 64~512（递减式设计）；
- 学习率：优先用 0.001（Adam），根据损失曲线调整（损失不下降则增大，震荡则减小）；
- Dropout 率：0.1~0.3（过高导致欠拟合）；
训练监控：实时监控训练 / 测试损失和准确率，出现过拟合（测试损失上升）时及时早停；
权重初始化：默认使用 PyTorch 内置初始化（如 He 初始化），无需手动调整；
硬件加速：使用 GPU 训练（PyTorch 自动支持），批量大小可适当增大（如 128、256），提升训练效率。

十、总结

深度神经网络（DNN）是深度学习的基石，其核心价值在于分层特征学习 和强大的非线性拟合能力。通过前向传播计算预测值、反向传播更新参数，DNN 能够处理各类复杂任务；结合 BatchNorm、Dropout、残差连接等技术，可有效解决训练中的梯度消失、过拟合等问题。

本文全面介绍了深度神经网络(DNN)的核心概念与应用。DNN通过多层隐藏层实现分层特征学习，底层提取低级特征，上层组合为高级语义特征。文章详细解析了DNN的网络结构(输入层、隐藏层、输出层)、激活函数选择(ReLU、Sigmoid等)、训练原理(前向传播和反向传播)，并提供了完整的Python实现代码。针对训练中的梯度消失、过拟合等问题，提出了ReLU激活函数、批量归一化、Dropout等解决方案。DNN广泛应用于图像识别、自然语言处理、推荐系统等领域，是CNN、RNN等现代深度学习模型的基础框架。实践时需注意数据预处理、超参数调优和训练监控等关键技巧。