目录

1.摘要
在按需配送场景中,实际需求常常偏离预期。本文研究了一种按需异构多无人机路径规划问题(ODHDRP):运输无人机在第一阶段将多架末端无人机投送至各子区域,末端无人机在第二阶段完成对子区域内客户的包裹配送,以实现规模经济。文章采用正态分布刻画客户需求,并构建了带机会约束的需求可靠性模型。为高效求解该问题,提出了一种混合迭代优化启发式方法(HIOH):首先,基于无人机载重设计聚类算法划分子区域,并利用动态规划生成初始路径;随后,通过结合启发式算子与可靠性策略的迭代优化算法,在满足机会约束的同时持续改进路径方案。
2.问题陈述和数学模型
针对按需异构多无人机路径规划问题(ODHDRP),本文构建了一个由一架运输无人机和多架末端无人机组成的两级配送系统。运输无人机从仓库出发,依次将末端无人机投放至各子区域,而末端无人机在单次飞行中完成子区域内多客户配送后前往自动化机场回收。由于客户实际需求事先不确定,需求偏差可能导致载重浪费或额外补给与配送成本。为刻画这一特性,假设客户需求服从正态分布,并设定运输无人机仅承担投放任务、末端无人机负责直接配送;当实际需求超过期望需求时,运输无人机需返回仓库补给。

客户需求在需求相对稳定的场景下假设服从正态分布,用以刻画多种随机因素叠加下的需求波动。运输无人机的期望运输量为:
ζ = ∑ i , j ∈ P l ζ j x i , j \zeta=\sum_{i,j\in P_l}\zeta_jx_{i,j} ζ=i,j∈Pl∑ζjxi,j
通过机会约束引入需求可靠性要求,在给定可靠性水平:
P r o ( ζ ≤ a d ) ≥ η \mathrm{Pro}(\zeta\leq ad)\geq\eta Pro(ζ≤ad)≥η
若 ζ ∼ N ( μ , σ 2 ) \zeta\sim N(\mu,\sigma^2) ζ∼N(μ,σ2),则其均值与方差分别为
μ = ∑ j ∈ P l μ j x i , j σ 2 = ∑ j ∈ P l σ j 2 x i , j \mu=\sum_{j\in P_l}\mu_j x_{i,j}\qquad \sigma^2=\sum_{j\in P_l}\sigma_j^2 x_{i,j} μ=j∈Pl∑μjxi,jσ2=j∈Pl∑σj2xi,j
在结构上,模型采用两级配送体系:第一级为运输无人机路径 R m R_m Rm,负责从仓库出发依次访问各子区域并投放末端无人机;第二级为末端无人机路径 R e R_e Re,在所属子区域内完成多客户配送后飞往自动化机场回收。最大化客户满意度:
f 1 = max ∑ k = 1 K ∑ i = 1 n k S ( e a i , k ) f_1=\max\sum_{k=1}^K\sum_{i=1}^{n_k}S(ea_{i,k}) f1=maxk=1∑Ki=1∑nkS(eai,k)
最小化系统总距离成本:
f 2 = min ( ρ 1 ∑ i , j d i , j x i , j + ρ 2 ∑ k = 1 K ∑ i , j d i , j y i , j , k ) f_2=\min\left(\rho_1\sum_{i,j}d_{i,j}x_{i,j}+\rho_2\sum_{k=1}^K\sum_{i,j}d_{i,j}y_{i,j,k}\right) f2=min(ρ1i,j∑di,jxi,j+ρ2k=1∑Ki,j∑di,jyi,j,k)
3.提出算法
针对大规模问题中精确算法效率受限的不足,本文提出了一种混合迭代优化启发式方法(HIOH)。该方法先通过考虑载重约束的改进 K-means 聚类与动态规划生成初始解,再在模拟退火框架下结合变量邻域下降、解扰动及多种启发式算子对路径进行迭代优化,并通过仓库插入策略处理需求可靠性的机会约束,从而在合理计算时间内获得高质量解。
初始解决方案策略
为提高求解效率,本文基于分而治之思想提出了一种考虑末端无人机载重约束的改进 K-means 聚类与初始解生成方法。首先利用 K-means 算法将客户节点划分为 K K K个子区域,其聚类目标函数与簇中心更新规则分别为:
J = ∑ i = 1 K ∑ z ∈ O i ∥ z i − v j ∥ 2 J=\sum_{i=1}^K\sum_{z\in O_i}\|z_i-v_j\|^2 J=i=1∑Kz∈Oi∑∥zi−vj∥2
v j = 1 ∣ O i ∣ ∑ z ∈ O i z v_j=\frac{1}{|O_i|}\sum_{z\in O_i}z vj=∣Oi∣1z∈Oi∑z
随后根据末端无人机载重 Q S Q_S QS对聚类结果进行调整,当子区域内需求 Q k Q_k Qk超载时,通过增加簇数或采用聚类
调整算子进行修正。完成聚类后,为每个子区域选择距离其簇中心最近的自动化机场作为回收点:
A k = arg min det ( O k c , A i ) , A i ∈ A A_k=\arg\min\det(O_k^c,A_i),A_i\in A Ak=argmindet(Okc,Ai),Ai∈A
考虑机会约束的迭代优化算法
为同时优化运输无人机与末端无人机路径并处理需求可靠性的机会约束,本文提出了一种基于模拟退火的迭代优化算法 VNSSA。算法以初始解 R 0 R_{0} R0为起点,通过变量邻域搜索生成新解,并在搜索过程中以一定概率接受劣解以跳出局部最优,其接受准则为:
r a n d o m ( ) < exp ( − f ∗ − f T ) \mathrm{random}()<\exp\left(-\frac{f^*-f}{T}\right) random()<exp(−Tf∗−f)
其中, f ∗ f^{*} f∗ 为新解目标函数值, f f f 为当前解目标函数值, T T T 为温度参数。
VNSSA 由解扰动与变量邻域下降两部分组成,并引入禁忌表以减少重复搜索。当新解不满足需求可靠性约束时,通过仓库插入(D-insert)算子使运输无人机返回仓库补给,从而恢复解的可行性。针对 ODHDRP 的结构特征,算法设计了起飞节点调整算子、节点交换算子和仓库插入算子,用于优化运输无人机的投放顺序及末端无人机的客户访问顺序。
基于需求可靠性的仓库插入策略
当实际需求 a d ad ad大于期望需求 e d ed ed时,原路径将不可行,运输无人机需返回仓库补给。为此,本文提出仓库插入策略 DRDIS ( D , R ) (\mathcal{D},R) (D,R)对不可行路径进行修复,并兼顾距离成本。若 a d > 2 × e d ad>2\times ed ad>2×ed,则根据剩余实际需求调整聚类与末端无人机路径,并在运输无人机路径中多次插入仓库节点以支持多次补给。
若 ed\
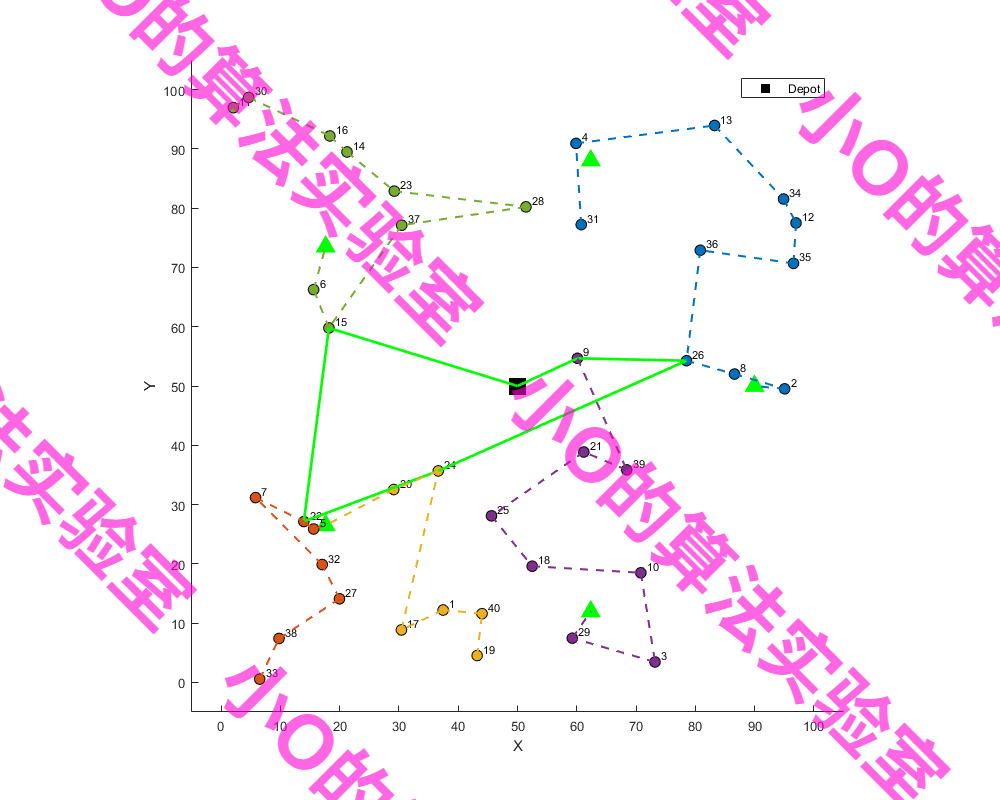
4.结果展示
5.参考文献
1\] Wen X, Cao Z, Xu S, et al. On-demand heterogeneous drone delivery problem\[J\]. International Journal of Production Research, 2025: 1-31. ### 6.代码获取 xx ### 7.算法辅导·应用定制·读者交流 xx