目录

1.摘要
为实现航天制造业生产过程的降本增效,本文建立了多目标柔性作业车间调度问题(MOFJSP)的数学模型,该模型综合考虑了四个优化目标:完工时间、刀具数量、机器负载以及机器能耗。为求解 MOFJSP,本文提出了一种改进基于分解的多目标进化算法(IMOEA/D)。为提升解的质量,算法在原有的替换操作基础上引入了另一种全局更新策略;种群初始化采用四种分配规则,并根据种群演化程度动态更新邻域结构。
2.MOFJSP问题描述
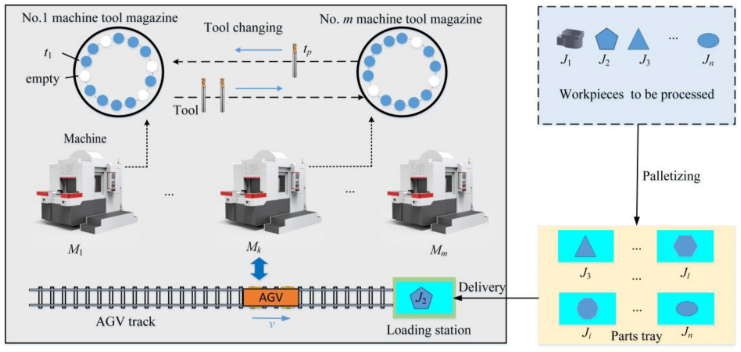
MOFJSP 描述在柔性制造系统中,为多工件、多机器安排加工工序的多目标调度问题。每个工件包含多道工序,可由不同机器加工且加工时间因机器而异,机器在加工前需装配工具,工序不可中断,同一时刻机器只能加工一道工序。调度的任务是为工序选择合适的机器并确定加工顺序,以优化多项性能指标。问题假设包括:初始时机器均可用、加工时间已知、作业间无优先级、运输与准备时间忽略等。

优化指标涉及加工时间、机器负荷、加工能耗和刀具数量:
min F = min ( C max , W T , N n T , E T ) \min F=\min(C_{\max},W_T,N_{nT},E_T) minF=min(Cmax,WT,NnT,ET)
C max = max 1 ⩽ i ⩽ n C i C_{\max}=\max_{1\leqslant i\leqslant n}C_i Cmax=1⩽i⩽nmaxCi
W T = ∑ k = 1 m ∑ i = 1 n ∑ j = 1 n i ( T i j k × x i j k ) W_T=\sum_{k=1}^m\sum_{i=1}^n\sum_{j=1}^{n_i}(T_{ijk}\times x_{ijk}) WT=k=1∑mi=1∑nj=1∑ni(Tijk×xijk)
E T = ( E 1 + E 2 ) E_T=(E_1+E_2) ET=(E1+E2)
其中, E 1 E_1 E1为车间机器的加工能耗, E 2 E_2 E2为车间机器的空转能耗。
E 1 = ∑ k = 1 m ∑ i = 1 n ∑ j = 1 n i ( P p e c k × T i j k × x i j k ) E_1=\sum_{k=1}^m\sum_{i=1}^n\sum_{j=1}^{n_i}(P_{pec}^k\times T_{ijk}\times x_{ijk}) E1=k=1∑mi=1∑nj=1∑ni(Ppeck×Tijk×xijk)
E 2 = ∑ k = 1 m ( P w e c k × t w k ) E_2=\sum_{k=1}^m(P_{wec}^k\times t_w^k) E2=k=1∑m(Pweck×twk)
3.改进IMOEA/D算法
IMOEA/D 在 MOEA/D 框架下,通过均匀权重向量将多目标问题分解为多个单目标子问题,并在其邻域内协同优化。
编解码方案
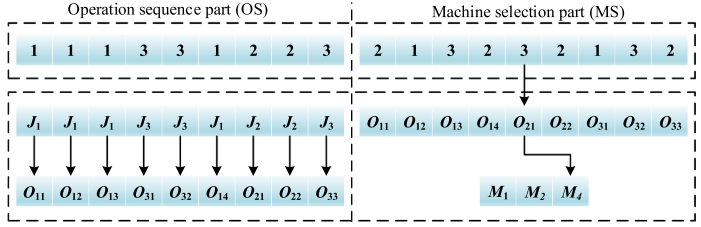
IMOEA/D 采用 MSOS 双层编码结构解决 MOFJSP,OS(Operation Sequence)层表示工序执行顺序;相同作业编号出现的次数对应其工序序号。MS(Machine Selection)层:表示每道工序所选机器;每个位置记录该工序对应的加工机器编号。两层长度一致,均等于总工序数。
在解码阶段,算法采用贪心插入式解码生成调度方案。为确保可能获得最优完工时间、并缩小搜索空间,采用只生成主动调度(active scheduling)方法,使每道工序在所选机器上的开工时间尽可能提前。
归一化切比雪夫聚合函数
在同时优化效率与成本等多类目标时,各目标量纲和数量级差异较大,会导致算法偏向优化数值较大的目标,从而影响解在 Pareto 前沿上的均匀分布。为此,IMOEA/D 对所有目标进行归一化处理,并采用归一化的 Tchebycheff 聚合函数以平衡不同目标的影响。
g t e f ( x ∣ λ i , z ∗ ) = max 1 ⩽ j ⩽ M { λ j i ∣ f j ( x ) − z ∗ z j max − z j ∗ ∣ } g^{tef}(x|\lambda^i,z^*)=\max_{1\leqslant j\leqslant M}\left\{\lambda_j^i\left|\frac{f_j(x)-z^*}{z_j^{\max}-z_j^*}\right|\right\} gtef(x∣λi,z∗)=1⩽j⩽Mmax{λji zjmax−zj∗fj(x)−z∗ }
IMOEA/D通过全局选择、局部选择、最短加工时间和随机选择四类策略按比例混合生成初始 MS 编码,使种群兼具质量与多样性,根据新旧解的改进程度动态调整邻域大小:改进大则缩小邻域以增强多样性,改进小则保持基准邻域,确保算法兼顾探索与收敛。
4.结果展示

5.参考文献
1\] Xiao B, Zhao Z, Wu Y, et al. An improved MOEA/D for multi-objective flexible job shop scheduling by considering efficiency and cost\[J\]. Computers \& Operations Research, 2024, 167: 106674. ### 6.代码获取 xx ### 7.算法辅导·应用定制·读者交流 xx